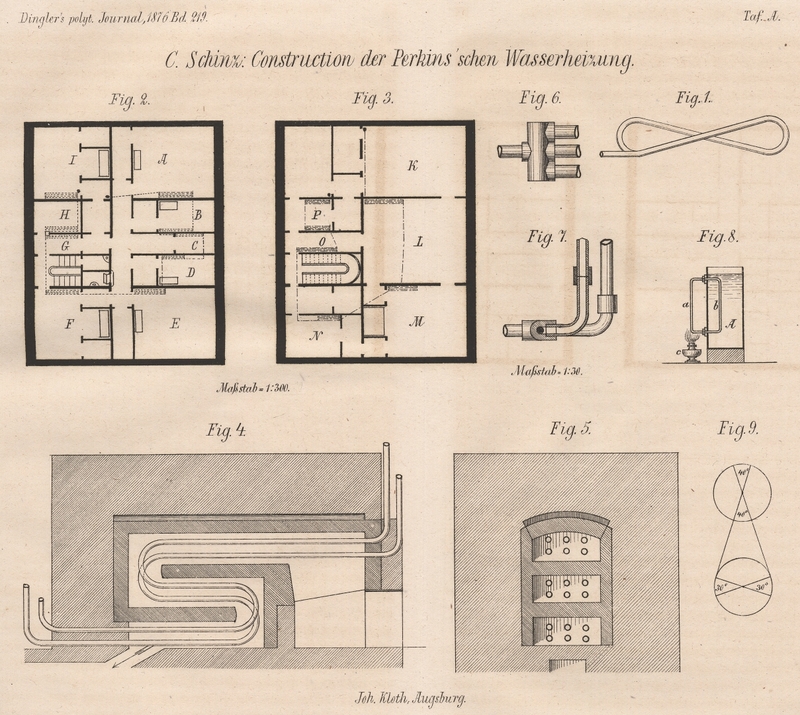
| Titel: | Construction der Perkins'schen Wasserheizung; von C. Schinz. |
| Fundstelle: | Band 219, Jahrgang 1876, S. 210 |
| Download: | XML |
Construction der Perkins'schen Wasserheizung; von C. Schinz.
Mit Abbildungen auf Texttafel A.
(Fortsetzung von S. 106 dieses Bandes.)
Schinz, über Construction der Perkins'schen
Wasserheizung.
Ofenconstruction.
Der größte Vorwurf, den man der Hochdruckwasserheizung mit Recht machen kann, ist
der, daß im Ofen eine sehr beträchtliche Wärmemenge zerstreut wird. Es stellt sich
daher die Aufgabe, einerseits den Ofen so anzubringen, daß die von ihm zerstreute
Wärme benützt werde, und anderseits die Menge auf ihr mögliches Minimum zu
beschränken.
Bezeichnen wir mit
T die Temperatur des Feuers im
Ofen,
r die Temperatur der äußern Luft,
welche den Ofen umspült,
S den Strahlungscoefficienten = 3,62
für Thonsteine,
L den Leitungscoefficienten = 1,778 für
horizontale Flächen,
= 2,05 für verticale Flächen,
C die Leitungsfähigkeit des Materials,
aus dem die Wände bestehen, für Thonsteine = 0,6,
e die Dicke der Ofenwände in Meter,
so läßt sich die äußere Temperatur τ' der Ofenflächen berechnen durch
Textabbildung Bd. 219, S. 210
Für Holz ist T = (1142 + 300)/2 =
721°, wenn die Gase mit 300° in den Kamin strömen.
Für Torf T = (1213 + 300)/2 =
756°
Für Braunkohle T = (1345 + 300)/2
= 822°.
Für Steinkohle T = (1409 + 300)/2
= 854°.
Da eine intensive Temperatur den Röhren zu gut kommt und diese mehr Wärme absorbiren
als der Ofen, so ist solche immer vortheilhafter.
Bei Anwendung dieser Brennstoffe würden die Temperaturen τ' sein:
für Ofendecke:
Textabbildung Bd. 219, S. 211
Ofendecke
e = 0,3
τ' =
209
219
237
246°
e = 0,6
129
135
145
150
Wände
e = 0,3
203
212
229
237
e = 0,6
125
130
140
145.
Die pro Stunde und Quadratmeter Fläche transmittirten Wärmeeinheiten sind dann:
Ofendecke
e = 0,3
2218
2425
2832
3054c
e = 0,6
956
1031
1161
1230
Wände
e = 0,3
2192
2377
2754
2946
e = 0,6
954
1017
1150
1219
Danach möchte man glauben, daß die größern Ofenwanddicken nicht einmal die Hälfte der
Wärme zerstreuen, als nur halb so dicke Wände; dem ist aber nicht so. Ein Ofen z.B.,
der 5m Seite und 4m Höhe hätte, würde eine Deckenfläche von
25qm darbieten und 80qm Wandfläche; machen wir nun aber e = 0,6 statt 0,3, so bekommt der Ofen 5m,6 Seite und 4m,3 Höhe, daher 32qm,4 Ofendecke und 96qm,4 Wandfläche, daher würde die
Transmission (für Steinkohle) sein:
für e =
0,3
e = 0,6
25 × 3054 =
76350
32,4 × 1230 =
39852
80 × 2946 =
235680
96,4 × 1219 =
117511
–––––––
–––––––
312030c
157363c
Verhältniß = 1 : 0,5.
Der in den Figuren
4 und 5 dargestellte Ofen hat nun 2m,64 Länge 1m,69 Breite und 1m,44 Höhe.
Daher ist dessen Deckenfläche = 2,64 × 1,69 =
4qm,461
Wandfläche (5,28 + 3,38) × 1,44 =
12qm,557. e = 0,6
und die Transmission =
4,461 × 1230 =
5487c
12,557 × 1219 =
15307
––––––
20794c.
Dies ist bedeutend mehr, als wir früher angenommen hatten;
dafür enthält aber auch der Ofen eine größere Röhrenlänge, es sind nämlich 6 Röhren
neben einander, von denen jede im Ofen 3m,870 Länge hat, also im Ganzen 3,87 × 6 = 23m,22.
Unter so veränderten Verhältnissen müssen wir nochmals prüfen, ob Brennstoffmenge und
erwarteter Effect übereinstimmen.
k
Wir haben
20794/6000 =
3,466
Steinkohle für die Ofentransmission und
67447/6000 =
11,214
Steinkohle für Erwärmung des Wassers,
––––––
zusammen
14,680,
welche zu 7509 = 110230c
geben.
Die specifische Wärme w des Productes ist = 14,68
× 5,3305 = 78c,251.
Die Progression der Ofentransmission = 1040 2599 4158 5717 u. 7276c.
Die Progression der Wassertemperaturen, wie früher = 60 98 136 174 u.
212°.
Der Absorptionscoefficient per Theil = W⁰ wird (23
× 22)/5 × 4,1964 = 19,488.
Wir haben daher
Wärmevorrath
T
t
T–t
Wasser-Absorpt.
Ofen-Transm.
Total.
110230
1400
212
1188
23151
7276
=
30427
79803
1020
174
846
16487
5717
=
22204
57599
736
136
600
11693
4158
=
15851
41748
510
98
412
8029
2599
=
10628
31120
398
60
338
5233
1040
=
6273
–––––––––––––––––––––––––––––––––––
24877
318
64593
20790
=
85383
Da die Evacuationstemperatur um 18° zu hoch ist, die Absorption aber um
2857c zu klein, so möchte es scheinen,
als ob auch diesmal noch mehr Transmissionsfläche erforderlich wäre; wir wollen aber
nun zeigen, daß eine kleine Vermehrung der Brennstoffe zu demselben Ziele führt.
Nehmen wir 15k Kohle, so wird der
Wärmevorrath = 112630c und die
Wärmecapacität der Gase = 15 × 5,3305 = 79,956, und wir haben dann:
112630
1400
212
1188
23151
7276
=
30427
82203
1028
174
854
16643
5717
=
22360
59843
749
136
613
11946
4158
=
16104
43739
547
98
449
8750
2599
=
11349
32390
405
60
345
6723
1040
=
7763
–––––––––––––––––––––
24627
308
67213
20790
=
88003
wodurch also unser Zweck ebenfalls erreicht wird, wenn auch
freilich mit etwas weniger Oekonomie.
Die Figuren 6
und 7 zeigen,
wie je 3 Röhren im Ofen außerhalb desselben verbunden werden können.
Statik der Widerstände im
Ofen.
Wenn schon die meisten Praktiker sich um diese Statik nicht im mindesten bekümmern,
so wird doch gerade die Aufstellung einer solchen denselben zeigen, daß dieselbe
nicht vernachlässigt werden darf, wenn man auf sichern Erfolg rechnen will, da viele
Fälle vorkommen, wo die Kammhöhe nicht ausreicht, um diese Widerstände zu überwinden, und anderseits
solche, wo der Ueberschuß der Kaminhöhe den Heizer verleitet, stärker zu feuern, als
dem Erfolge und der Oekonomie zuträglich ist.
15k Kohle, welche pro Stunde verbrannt
werden, geben 15 × 16,595 = 248cbm,87 Gase von 0°, entsprechend = 0cbm,0691 pro Secunde. Dieses Volum ist aber durch Erhöhung der Temperatur
im Ofen weit größer, wechselt übrigens jeden Augenblick, sowie die Gase sich
abkühlen. Wir können nach den obigen Resultaten annehmen, daß sie in den 5 Sectionen
successive die Temperatur 1400 1030 640 450 und 300° haben werden. Dadurch
werden die Volume V (in Cubikmeter) dieser Gase pro
Secunde = 0,4238 0,3301 0,2313 0,1831 0,1451.
Die Querschnitte Q der 3 Canäle im Ofen berechnen sich,
indem wir deren Höhe mit der Breite multipliciren und vom Producte für die Röhren 6
× 0,045² × π = 0,00954
abziehen.
0,08846 0,07866 und 0,7866 = Q.
Nun sind die Geschwindigkeiten v = V/Q
in der 1. Section 0,4238 : 0,08846 = 4m,79, dann
in der 2. Section 0,3301 : 0,08846 = 3m,73,
in der 3. 0,2313 : 0,07866 = 2m,94,
in der 4. 0,1831 : 0,07866 = 2m,33 und
in der 5. 0,1451 : 0,07866 = 1m,84,
im Fuchse 0,1451 : 0,049 = 2m,96 und
im Kamine 0,1451 : 0,0784 = 1m,85, wenn dessen Durchmesser 0m,28 ist.
Diesen Geschwindigkeiten entsprechen die Druckhöhen:
p₁ = 1,17; p₂ = 0,717; p₃
= 0,443; p₄ = 0,281; p₁ = 0,174; p₆ = 0,444 und p₇ 0,174.
Der am schwierigsten zu bestimmende Widerstand ist der, welcher im Brennstoffe auf
dem Roste stattfindet, da er von der Art und der Zertheilung von jenem abhängt.
Backende pulverförmige Steinkohlen geben den größten
Widerstand; annähernd ist w = 0,1 p₁, =
0,1170
Die Umbiegung der Gase in den Canal im scharfen rechten
Winkel p₁ =
1,1700
Die Contraction im Eingange (Heizung und Ventilation, S. 333
Formel 6.) D = 0,55 d = 0,2, A = 0,42 und Ap =
0,4680
Die Reibung im 1. Canale
KLU/4S × (p₁ + p₂/2) = (0,024 × 0,88 ×
2,09)/(4 × 0,08846) × 0,943 =
0,1176
––––––
Summe
1,8726
Uebertrag
1,8726
U ist gleich dem Umfange der
Canalwände plus demjenigen des Umfanges
der 6 Röhren.
Im 2. Canale ist die Reibung (K
× 0,56 × 2,15)/(4 × 0,07866) p₃ =
0,0407
Im 3. Canale (K × 0,56
× 2,15)/(4 × 0,07866) p₄ =
0,0258
Die doppelte Umbiegung in scharfen rechten Winkeln zwischen
dem
1. und 2. Canale (p₂ + p₃)/2 + (0,717 + 0,433)/2 =
0,5800
dem 2. und 3. Canale (p₃ + p₄)/2 = (0,443 + 0,281)/2 =
0,3620
Die Umbiegung durch den Fuchs p₅ sin² i = 0,174 × 0,7071² . (i = 45°) =
0,0870
Die Contraction in demselben A =
0,45 p₆ = 0,45 × 0,444 =
0,1998
––––––
3,1679
Nun fragen wir, wie hoch muß der Kamin sein, um diesen Widerstand
zu überwinden, wenn die Temperatur der Gase in demselben = 300°?
Diese Höhe ist = h = P/(1 – sy), wo P = dem Widerstande, s = dem
specifischen Gewichte der Gase nach ihrer Temperatur = 0,4763 und y = dem specifischen Gewicht nach ihrer Natur = 1,03508.
3,1679/(1 – 0,4763 × 1,02508) = h = 6m,19. In unserm vorliegenden Projecte wird
aber der Kamin wohl 12m Höhe haben; wenn
aber dies anders wäre, so müßte man suchen, welches die nothwendige Höhe ist.
Die Umbiegung in den Kamin verbraucht noch an Druckhöhe p₇ =
0,1740
Die Reibung im Kamine, incl. Zuführungscanal, den wir = 2mannehmen. = KL/D
p₇ = (0,024 × (12 + 2))/0,28
× 0,174 =
0,2088
Effective Ausflußgeschwindigkeit
0,1740
––––––
3,7347
Nun producirt aber unser Kamin P
= h – hsy =
6,1416
und wir haben einen Drucküberschuß von
der auf irgend eine Weise zu beseitigen
ist.
2,4169
Gewöhnlich geschieht das mittels eines Schiebers, den man zwischen Kamin und Ofen
anbringt. Dies hat aber den Nachtheil, daß der Heizer nie auf einen bestimmten
Consum rechnen kann, daher er seine Röhren bald überhitzt, bald nicht genügend
erwärmt. Damit also der richtige Maßstab inne gehalten werden könne, soll der
Widerstand ein permanenter und unveränderlicher sein.
Nichts ist zu diesem Zwecke geeigneter, als eine conische oder pyramidale Verengung
des Kamins. (Heizung und Ventilation, Formel 5.) Machen wir die Pyramide in einem
Winkel von 30°, so ist A = 0,26. Daher ist 0,26
× p = 2,4169;
p = 2,4169/0,26 = 9,32, daraus v = √2gp = 13m,511,
dann Q = V/v = 0,1451/13,511 = 0,01074 = Querschnitt
der conischen oder pyramidalen Kaminspitze, durch welche der Ueberschuß von p = 2,4169 absorbirt wird, so daß der Kohlenconsum fast sicher
constant 15k pro Stunde bleibt. Diese
Ausströmungsgeschwindigkeit wäre allenfalls durch ein Manometer zu controliren, um
sich zu versichern, daß richtig gerechnet wurde; es müßte dasselbe einen Druck von
0m,0121 Wasser geben.
In einem solchen Falle könnte man allerdings durch Verlängerung der Ofenröhren auch
noch die Evacuationstemperatur vermindern, um damit eine Ersparniß an Brennstoff zu
erhalten. Durch Zufügen von 2 Röhren zu den 6 vorhandenen, würde der Consum sich auf
13k Kohle reduciren lassen. Die
Evacuationstemperatur würde dann 1300, welcher s =
0,6773 entspricht, daher dann p = 3,87, was so ziemlich
den Widerständen entspricht, da einerseits die Volume der Gase kleiner, aber auch
die Querschnitte kleiner werden.
Es wird also immer zweckmäßig sein, hohe Schornsteine zur Oekonomie des
Brennmaterials zu benützen, wo solche ohnedem von der Localität gegeben sind. Wäre
hingegen ein solcher Kamin besonders zu construiren, so würden die größern
Constructionskosten den Ersparnissen von 3 Jahren gleichkommen.
Tabelle I.
Allgemeine Werthe und Bedeutung der in dieser Abhandlung
gebrauchten algebraischen Zeichen.
D und d Durchmesser,
größerer und kleinerer, insofern deren zwei in Betracht kommen.
S Strahlungscoefficient.
Q Querschnitt.
F Oberfläche.
W Wärmetransmissionscoefficient an Luft, wenn t' – t = 20°,
pro 1m laufende Röhre.
W° Wärmeaufnahme des Wassers pro 1m laufende Röhre.
w Specifische Wärme der Verbrennungsproducte.
v Geschwindigkeit.
h Höhe, auch Fallhöhe.
s Specifisches Gewicht der Luft oder des Wassers.
c Wärmeeinheit.
Dimensionen der jetzt gebräuchlichen
Perkins'schen Röhren.
D Aeußerer Durchmesser = 0m,045, daher Oberfläche F pro laufenden Meter = 0,045 π = 0qm,1414.
d Innerer Durchmesser = 0m,024, daher innerer Querschnitt Q = 0,012² π =
0qm,000113.
W⁰ Wärmeaufnahme im Ofen vom Wasser pro 1qm = 59c,3555, daher pro 1m laufende
Röhre = 59,3555 × 0,1414 = 4c,1964.
Textabbildung Bd. 219, S. 215 Formel zur Berechnung der Geschwindigkeit.
2g Intensität des Falles = 19m,61.
P = h (s – s') Druckhöhe
oder auch Fallhöhe.
L Länge der Röhren, in denen Reibung stattfindet. Diese
Reibung ist eigentlich KL/d.
K Reibungscoefficient = 0,024; da d ebenfalls für unsere Röhren = 0,024 ist, so wird der Bruch K/d = 1.
B Umbiegungen im rechten Winkel = 1 oder 0,5, wenn
abgerundet.
Tabelle II.
Transmissions-Coefficienten
für die Temperatur der Luft. Summen der Coefficienten Ca, aus welchen
der mittlere Coefficient = W erhalten wird, indem man
die 10gradigen Temperaturintervallen darin dividirt. Absorptionscoefficienten der
Ofenröhren
Textabbildung Bd. 219, S. 216
Textabbildung Bd. 219, S. 216
Temperatur des Wassers t.;
Entsprechende Transmission pro 1m Röhre C;
Mittlerer Transmissionscoefficient Ca; Summe von Ca; Temperaturintervalle;
Mittlerer Coefficient W für das System.
Tabelle III.
Specifisches Gewicht des Wassers bei Temperaturen zwischen
0° und 300°.
t⁰
0
1
2
3
4
5
6
7
8
9
0
1,00000
0,99954
0,99908
0,99862
0,99814
0,99768
0,99722
0,99676
0,99630
0,99582
10
0,99536
99490
99444
99399
99353
99305
99259
99213
99168
99122
20
99076
99031
98985
98940
98894
98848
98803
98757
98712
98667
30
98621
98576
98530
98485
98440
98394
98349
98304
98261
98216
40
98170
98125
98080
98035
97992
97947
97902
97857
97812
97769
50
97724
97679
97634
97589
97546
97501
97456
97414
97369
97324
60
97279
97237
97192
97149
97105
97060
97017
96973
96928
96886
70
96841
96796
96754
96710
96668
96623
96581
96536
96492
96450
80
96405
96363
96319
96276
96234
96190
96148
96104
96062
96017
90
95975
95933
95889
95847
95803
95761
95717
95675
95633
95592
100
95548
95506
95464
95420
95378
95334
95293
95251
95209
95166
110
95124
95082
95039
94997
94955
94936
94872
94831
94787
94746
120
94704
94663
94626
94578
94537
94495
94454
94413
94371
94330
130
94289
94248
94206
94165
94122
94081
94039
93998
93957
93916
140
93875
93834
93793
93752
93711
93670
93629
93588
93549
93508
150
93467
93426
93386
93345
93304
93263
93222
93182
93143
93102
160
93062
93021
92980
92942
92901
92860
92820
92781
92741
92700
170
92660
92621
92581
92540
92500
92459
92421
92380
92342
92302
180
92264
92223
92183
92143
92102
92064
92024
91984
91945
91906
190
91867
91827
91787
91749
91709
91671
91631
91593
91552
91515
200
91474
91437
91397
91359
91319
91281
91241
91201
91163
91126
210
91086
91048
91008
90970
90933
90893
90855
90816
90778
90740
220
90701
90663
90625
90586
90548
90511
90471
90434
90396
90357
230
90319
90282
90244
90205
90168
90130
90093
90053
90009
89979
240
89941
89904
89865
89828
89791
89753
89716
89679
89640
89602
250
89565
89528
89491
89455
89417
89380
89343
89304
89267
89230
260
89193
89156
89119
89082
89045
89008
88971
88934
88898
88861
270
88824
88787
88750
88714
88677
88640
88603
88567
88532
88495
280
88459
88422
88385
88349
88312
88276
88239
88204
88168
88131
290
88095
88058
88022
87987
87951
87914
87878
87842
87807
87771
300
87734
Tabelle IV.
Specifisches Gewicht der Gase = 1, bei Temperaturen zwischen
0° und 300°, oder Werthe für s von
0° bis 300° zur Berechnung der Volume und der Höhendifferenzen von
Luftsäulen bei verschiedenen Temperaturen.
t⁰
0
1
2
3
4
5
6
7
8
9
0
1,00000
0,99963
0,99273
0,98912
0,98555
0,98200
0,97858
0,97499
0,97152
0,96808
10
0,96465
96126
95788
95453
95120
94789
94460
94135
93810
93704
20
93171
92854
92538
92225
91916
91607
91300
90996
90692
90392
30
90095
89797
89504
89211
88920
88630
88345
88058
87775
87494
40
87215
86936
86660
86385
86113
85842
85574
85306
85039
84775
50
84512
84252
83990
83736
83480
83224
82972
82720
82469
82222
60
81975
81728
81484
81242
81001
80761
80521
80286
80050
79816
70
79583
79352
79121
78893
78665
78439
78215
77990
77768
77548
80
77327
77110
76892
76676
76461
76247
76034
75823
75614
75405
90
75197
74990
74784
74580
74377
74174
73972
73773
73575
73377
100
73180
72984
72788
72596
72404
72212
72021
71831
71643
71455
110
71268
71082
70897
70715
70531
70349
70170
69989
69809
69632
120
69438
69279
69102
68927
68754
68581
68408
68239
68068
67898
130
67730
67563
67395
67230
67064
66901
66736
66573
66410
66250
140
66089
65930
65772
65613
65456
65298
65142
64988
64834
64680
150
64527
64374
64223
64072
63928
63772
63624
63476
63314
63182
160
63036
62890
62754
62602
62458
62316
62173
62033
61893
61752
170
61613
61474
61335
61198
61059
60924
60787
60654
60519
60385
180
60252
60120
59986
59855
59724
59594
59463
59335
59205
59077
190
58950
58823
58696
58571
58445
58320
58196
58072
57948
57825
200
57703
57581
57459
57339
57219
57099
56980
56862
56743
56625
210
56508
56391
56274
56160
56044
55929
55815
55701
55588
55487
220
55362
55250
55028
54916
54916
54806
54695
54586
54478
54369
230
54260
54153
54046
53939
53832
53727
53620
53526
53411
53306
240
53202
53099
52997
52894
52791
52689
52587
52487
52385
52285
250
52186
52086
51986
51887
51789
51690
51593
51496
51399
51303
260
51206
51111
51014
50919
50824
50729
50635
50542
50449
50356
270
50236
50171
50078
49986
49895
49805
49713
49623
49532
49442
280
49354
49265
49176
49087
48999
48911
48824
48736
48650
48562
290
48476
48390
48305
48219
48134
48048
47966
47881
47797
47713
300
47630
Tabelle V.
Zusammensetzung, Wärmeproduction, Bedarf an Luft zur Verbrennung,
specifische Wärme der Verbrennungsproducte bei 0° und absolutes und
specifisches Gewicht derselben für verschiedene Brennstoffe.
Vollkommene Verbrennung mit Luftüberschuß.
Zusammensetzung.
Holz.
Torf.
Braunkohle
Steinkohle.
Anthracit.
Asche
k
–
0,0480
0,0930
0,0520
0,0280
Elemente des Wassers u. Stickstoff
k
0,6000
0,5075
0,2669
0,0973
0,0332
Freier Wasserstoff
k
0,0056
0,0117
0,0202
0,0358
0,0234
Kohlenstoff
k
0,3944
0,4328
0,6169
0,8149
0,9154
Wärmeproduction.
Aus Wasserstoff zu 34000c
c
190
398
687
1217
796
Aus Kohlenstoff zu 8000c
c
3155
3462
4935
6519
7323
––––––––––––––––––––––––––––––––––––––––––––––––––
3345
3860
5622
7736
8119
Minus latente Wärme des Wassergases zu
540c
c
351
331
244
227
132
––––––––––––––––––––––––––––––––––––––––––––––––––
Effective erzeugte Wärme
c
2994
3529
5378
7509
7987
Bedarf an
Sauerstoff u.Luft zur
Verbrennung.
Sauerstoff zur Bildung von
Kohlensäure
k
1,0517
1,1541
1,6451
2,1731
2,4411
Sauerstoff zur Bildung von Wasser
k
0,0448
0,0936
0,1616
0,2864
0,1872
Mitgehender Stickstoff
k
3,6096
4,1073
5,9475
8,0964
8,6521
Luftüberschuß = 1/2
k
4,7061
5,3550
7,7542
10,5559
11,2804
––––––––––––––––––––––––––––––––––––––––––––––––––
Total
k
9,4122
10,7100
15,5084
21,1118
22,5608
Specifische Wärme
derVerbrennungsproducte.
Kohlensäure c
c
0,31294
0,34341
0,48950
0,64660
0,72635
Wassergas c
c
0,30847
0,29108
0,21456
0,19926
0,11581
Stickstoff c
c
0,88074
1,00218
1,45119
1,97552
2,11121
Luftüberschuß c
c
1,11864
1,27288
1,84317
2,50913
2,68135
––––––––––––––––––––––––––––––––––––––––––––––––––
Total
c
2,62079
2,90955
3,99842
5,33051
5,63472
Initialtemperaturen.
Grad
1142
1213
1345
1409
1417
Volum d. nöthigen Luft bei 0⁰
cbm
7,2452
8,2442
11,938
16,251
17,362
Volum der Gase bei 0⁰
cbm
8,01404
8,99362
12,3805
16,59494
17,53106
Specifisches Gewicht y
der Gase bei 0⁰, Luft = 1
0,99999
1,00483
1,02059
1,02508
1,03340
(Fortsetzung folgt.)
Tafeln