| Titel: | Construction der Perkins'schen Wasserheizung; von C. Schinz. |
| Fundstelle: | Band 219, Jahrgang 1876, S. 97 |
| Download: | XML |
Construction der Perkins'schen Wasserheizung; von
C. Schinz.
Mit Abbildungen auf Texttafel A.
(Fortsetzung von S. 72 dieses Bandes.)
Schinz, über Construction der Perkins'schen
Wasserheizung.
Transmissionsröhren.
Transmissionsröhren nennen wir denjenigen Theil eines Röhrensystems, welches die
Wärme in den zu beheizenden Röhren abgibt, während eine andere Röhrenlänge des
Systems dazu bestimmt ist, im Ofen Wärme aus dem Feuer aufzunehmen. Ferner ist eine
gewisse Länge des Systems nothwendig, um das heiße Wasser aus dem Ofen in die Zimmer
und das in denselben abgekühlte in den Ofen zurück zu führen.
Jedes System theilt sich also in: Transmissionsröhren, Ofenröhren und
Leitungsröhren.
Transmissionscoefficient nennt man diejenige Wärmemenge, die ein erwärmter Körper in
der Zeiteinheit einer Stunde an die ihn umgebende Luft abzugeben vermag, je nach der
Temperaturdifferenz t – T zwischen dem Wärme
abgebenden Körper und der Wärme aufnehmenden Luft, t ist
dann in unserm Falle gleich der Temperatur des Wassers und T = derjenigen der Luft.
Soll diese auf 20° erwärmt werden, so ist T = 20°, und T wird abhängen
von der vorhergehenden Abkühlung des Wassers. Wenn z.B. die Initialtemperatur des
Wassers t'' = 250° ist, so wird die erste
Röhrenlänge (siehe Tabelle II) einen Transmissionscoefficienten haben, der zwischen
427,5 und 474,5 liegt; er wird also 451c
sein. Wie lang dieses Röhrenstück sein dürfe, hängt von der Geschwindigkeit der
Circulation in den Röhren ab. Wenn das Wasser mit 250° aus dem Ofen kommt und
mit 60° in denselben zurückkehren soll, so haben wir successive 20
verschiedene Transmissionscoefficienten, deren Summe gleich ist der durch die ganze
Röhrenlänge abgegebenen Wärme. Es ist klar, daß das Wasser aus dem Ofen eben so
viele Wärmeeinheiten enthalten muß. Damit es aber diese enthalten könne, ist
nothwendig, daß es mit einer gewissen Geschwindigkeit durch den Ofen ströme. Die
Transmissionsröhre wird daher um so länger sein dürfen, als die Circulation
lebhafter ist; z.B. darf die Röhre nur 163m
Länge haben, wenn die
Geschwindigkeit des Wassers = 0m,1127 pro
Secunde ist, und 188m Länge, wenn die
Geschwindigkeit 0m,1287 wird. Im erstern
Falle ist die Summe der transmittirten Wärme = 34700c, im letztern aber 39900c.
Sämmtliche Transmissionscoefficienten in der Tabelle gelten für 1m Röhrenlänge von 45mm äußerm Durchmesser und unter der
Bedingung, daß diese Röhre horizontal liege und frei von der Luft umspült werden
könne. Diese Coefficienten würden andere werden, wenn die Röhre senkrecht gestellt
wäre, oder wenn sie einen andern Durchmesser hätte; z.B. eine horizontale Röhre von
nur 15mm Weite würde für t – T = 190° 2943c statt 4150c für 45mm Durchmesser pro 1qm geben.
Ebenso würde dieselbe Röhre von 10mm
Durchmesser, wenn sie 12m hoch senkrecht
aufgestellt wäre, nur den Coefficienten 3589c pro 1qm geben. So können auch
dicht auf einander geschichtete Röhren, wie man sie gewöhnlich in den Zimmerspiralen
findet, nur kleine Coefficienten geben, da die an der untersten Röhre erwärmte Luft
schon mit einer erhöhten Temperatur an die über ihr liegende Röhre tritt, und da
überhaupt solche Röhren nur von der Seite von Luft bespült werden.
Weit besser wäre es in den meisten Fällen, gar keine Spiralen zu machen, sondern die
Röhren einfach auf oder in den Boden zu legen, da diese Krümmungen die Circulation
des Wassers sehr beeinträchtigen. Will man aber durchaus solche Wärmeschränke haben,
so sorge man dafür, daß wenigstens die größtmögliche Transmission stattfinde, denn
sonst ist es weder möglich, unnütze Röhrenlängen zu vermeiden, noch eine richtige
Vertheilung der Transmissionsröhren in verschiedenen Räumen vorzunehmen. Man müßte
die Spiralen spiralförmig gestalten oder neben einander senkrecht liegend wie in
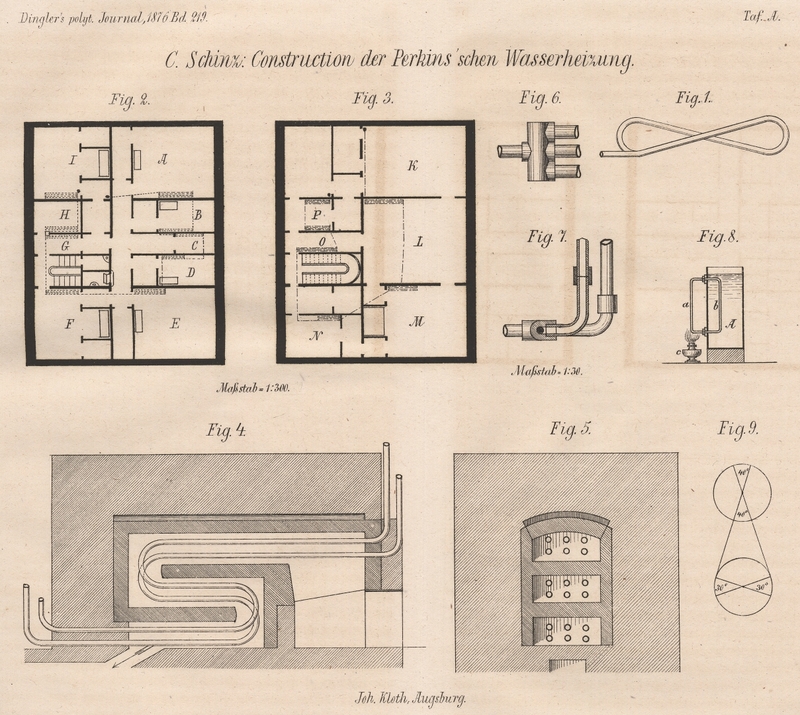
Figur 1
anordnen, so daß die Luft überall frei zutreten kann und nicht vorerwärmte Luft an
die Röhren trete.
Wie man den Bedarf an Wärme für jeden einzelnen zu heizenden Raum für den
Maximumsbedarf bestimmt, habe ich in meinen frühern Schriften so umständlich
angegeben, daß hier eine Wiederholung jener Anleitung überflüssig wäre.
Wäre nun die Summe der in verschiedene Räume zu vertheilende Wärmeeinheiten = 67
447c, und wir wollen den Röhren die
möglichst größte Leistung zumuthen, so geben wir dem Wasser im Ofen 250° und
führen dasselbe mit 60° zurück; dann ist der mittlere
Transmissionscoefficient W nach Tabelle II = 2125c, und wir brauchen 67447 : 2125 = 317m,4 Transmissionsröhren im Ganzen. Nun
könnten wir aber nur in Ausnahmsfällen eine so große Circulationsgeschwindigkeit
hervorbringen, um dieser
Länge zu genügen. Wir müssen daher diese Länge in zwei gleiche Hälften theilen und
mit denselben zwei Systeme bilden, so daß wir zwei Transmissionsröhren von 158m,7 Länge bekommen, in welchen das Wasser
mit 250° eintritt und mit 60° austritt. Nun durchläuft das Wasser nach
unserer Tabelle 19 Temperaturintervalle und jeder der 19 Coefficienten gilt für
158,7 : 19 = 8m,35 Röhrenlänge.
Diese 19 Stück Röhrenlängen von 8m,35 werden
also, insofern wir die richtige Circulationsgeschwindigkeit haben,
transmittiren:
451,0 × 8,35
3767c
410,1
3424
376,5
3144
345,2
2882
315,8
2637
288,2
2357
262,2
2144
237,7
1944
214,7
1756
192,9
1577
172,5
1411
153,2
1253
135,0
1104
117,9
964
101,7
832
86,5
707
72,1
590
58,6
479
46,0
376
––––––
Summe
33339c,
was mit der Hälfte des ganzen Bedarfes 67447 : 2 =
33723° hinlänglich nahe stimmt.
Mittels dieser Werthe können wir nun leicht die Vertheilung der 317m Transmissionsröhren vornehmen. Wir wollen
dies für eine städtische Privatwohnung vornehmen, wie sie in Fig. 2 und 3 als Grundrisse für zwei
Stockwerke angegeben. Der Wärmebedarf für die einzelnen Räume wird in folgendem
angegeben. Wir berechnen dann den Röhrenbedarf für jeden einzelnen aus obigen Zahlen
und erhalten:
Bedarf fürdie Räume
TotaleRöhrenlänge
Röhrenlängeaus obigenWerthen
Transmission
c
m
m
c
c
A
5793
14,442
8,350
3767
6,092
2026
5793
B
2907
6,183
2,258
1398
3,925
1509
2907
C
2907
8,035
4,425
1635
3,610
1272
2907
D
2907
8,762
4,740
1610
4,022
1297
2907
E
5793
20,853
4,508
1340
8,350
2357
7,995
2096
5793
F
5793
27,578
0,355
48
8,350
1944
8,350
1756
8,350
1577
2,173
468
5793
G
2907
19,794
6,177
943
8,350
1253
5,267
711
2907
H
2733
26,076
3,083
393
8,350
964
8,350
832
6,293
544
2733
I
5793
27,107
2,057
163
+ 9,349
8,350
590
8,350
479
Röhre des 2. Systems
8,350
376
8,350
3767
0,999
418
5793
K
5793
14,610
7,351
3006
7,250
2787
5793
L
8745
28,272
1,100
357
8,350
2882
8,350
2637
8,350
2357
2,122
512
8745
M
5793
25,320
6,228
1632
8,350
1944
8,350
1756
2,392
461
5793
––––––––––––––––––––––––––––––––––––––––––––––
Uebertrag
236,381
57864
Bedarf fürdie Räume
TotaleRöhrenlänge
Röhrenlängenaus obigenWerthen
Transmission
c
m
m
c
c
Uebertrag
236,381
57864
N
3024
17,721
5,958
1116
8,350
1411
3,413
497
3024
O
2733
20,697
4,937
756
8,350
1104
7,410
873
2733
P
3075
42,690
0,940
91
8,350
832
8,350
707
8,350
590
8,350
479
8,350
376
3075
––––––––––––––––––––––––––––––––––––––––––––––
Summe
317,489
66696.
Danach berechnen sich dann auch die Spiralen, die in jeden Raum kommen, insofern man
solche zu haben wünscht. Wir wollen zuerst ausrechnen, wie viele Spiralen
gewöhnlicher Form wir haben müßten und dann solche in der Form der Figur 1. Erstere haben
0m,15 Biegung und zwei gerade Röhren je
1m,2 lang, daher ist deren totale Länge
2m,85; die letztern
d =
0,4
0,35
0,30
0,25.
Länge der geraden Stücke je 1m,
somit
3,20
3,05
2,90 u.
2,75
Länge der Spiralen.
Raum
ErforderlicheRöhrenlänge
Zahl der üblichenSpiralen
Zahl der SpiralenFig. 1
d
A
14,44
5
5
0,3
B
6,18
2
2
0,3
C
8,03
3
3
0,25
D
8,76
3
3
0,3
E
20,85
7
7
0,3
F
27,58
9
9
0,35
G
19,79
7
3
0,35
H
26,07
9
9
0,3
I
27,11
9
9
0,35
J
9,35
3
3
1/2
0,3
K
14,60
5
5
0,3
L
28,27
10
9
0,4
M
25,32
9
8
0,4
N
17,72
6
6
1/2
0,3
O
20,69
7
7
0,3
P
42,69
15
14
0,35
Zahl der Spiralen
109
103
Nun hat jede dieser Spiralen 4 Biegungen im rechten abgerundeten Winkel, was einen
sehr bedeutenden Biegungswiderstand für das Wasser in den Röhren ausmacht; würden
hingegen diese Röhren nur blos einfach in den Boden gelegt, so würde nicht nur
dieser Widerstand sich sehr bedeutend reduciren, sondern wir würden auch noch viel
weniger Leitungsröhren bedürfen. Es kommt übrigens ganz darauf an, ob die disponible
Kraft zur nothwendigen Circulationsgeschwindigkeit vorhanden ist; wäre dies nicht
der Fall, so müßte man nothwendig auf alle Spiralen verzichten. Immerhin aber werden
die verticalen Spiralen Fig. 1 den Vorzug
verdienen, denn wenn, wie ich gezeigt habe, der Transmissionscoefficient für auf
einander gewundene Spiralen sehr viel kleiner wird, so müßten wir unbezweifelt die
Zahl derselben noch um V 1/3, vielleicht sogar um 1/2 vermehren, wodurch nicht blos
die Reibung es auch würde, sondern auch die Länge von 317m Röhren auf 423 bis 475 anwachsen würde.
Daraus erklärt sich auch, warum die Praktiker viel mehr Röhren brauchen, als
nothwendig wäre, und warum dieses Heizsystem viel mehr kostet, als es kosten sollte,
und wie wenig der Empiriker auf sichern Erfolg rechnen kann.
Wenn auch behauptet wird, man mache den Apparat mit mittlerm Drucke, so ist das nur
eine Täuschung, wenigstens gewiß in den meisten Fällen; denn bei so langen Röhren
ohne sehr große Steighöhe kann irgend eine Circulation nur zu Stande kommen, indem
man dem Wasser ursprünglich eine hohe Temperatur gibt, obgleich man als mittlere
Transmission pro 1m nicht mehr als 100c erwartet und vielleicht, wenn es gut
geht, auch erhält.
Wohlfeil wird man nur construiren, wenn man pro 1m auf 212c,5 im Mittel rechnet,
und es wird dann auch leichter sein, die nöthige Circulation zu erhalten.
Wärme-Aufnahme des Wassers im
Ofen.
Ofen-Röhren.
Es scheint von Anfang an bei den Herstellern von Perkins'schen Wasserheizungen eine
fixe Idee gewesen zu sein, daß die Röhren wo immer thunlich in Spiralen dicht auf
einander und über einander gewunden werden müssen. Um dieser Idee willen sind viele
Tausende von Metern solcher Röhren ganz unnütz, ja oft zum Nachtheile des Erfolges
verwendet worden, denn so aufgewundene Röhren können weder alle Wärme abgeben, noch
alle Wärme aufnehmen, die ihrer Transmission oder ihrer Heizfläche zukommt. Daher
gilt bei den Praktikern die unverbrüchliche Regel, daß man 1/6 bis 1/5 der
Gesammtröhrenlänge in den Ofen legen müsse. Es ist aber eine sonst ausgemachte Sache, daß 1qm Heizfläche pro Stunde 59c,355 für eine Differenz von T – t = 1° pro
Stunde aufnimmt. Wenn daher 1m Röhre 0qm,1414 Fläche darbietet, so wird ein
solcher für T – t
ebenfalls = 1°, 59c,355 ×
0,1414 = 4c,1964 =
W° aufnehmen – dies aber allerdings unter der Bedingung, daß
diese Röhre vom Feuer frei und an deren ganzem Umfange bespült werde. Dieser
Bedingung wird nun aber bei der üblichen Construction auf keine Weise Genüge
geleistet. Daher kommt es dann auch, daß gewöhnlich eine 6mal größere Röhrenlänge
als erforderlich in den Ofen gelegt wird. Es läßt sich die nothwendige Länge der
Ofenröhren leicht bestimmen, indem man den Wärmebedarf durch obige Zahl W° ×T –
t = dividirt. Ist T' die Initialtemperatur der
Gase, T'' die Endtemperatur derselben, die des Wassers
in den Röhren = t' bez. t'',
so ist T – t = (T' +
T'')/2 – (t' +
t'')/2. Wenn nun T' =
1400, T'' = 300, t' = 60,
t'' = 250 sind, so wird T
– t = 695°, und wenn nun die in den Räumen zu vertheilende
Wärmemenge wie in unserm Projecte 67447c
beträgt, so wird die Länge der Ofenröhre = 67447 : (695 × 4,1964) = 23m,126.
Dies wäre sogar ganz genau, wenn nicht der Ofen selbst ebenfalls aus dem Herde und
den Canälen Wärme aufnehmen und an die äußere Luft zerstreuen würde; dadurch wird
aber die mittlere Differenz T – t eine andere
selbst dann, wenn der Brennstoffconsum Ersatz bietet für das, was im Ofen abgeht.
Man muß daher die so gefundene Ofenröhrenlänge stets controliren.
Diese Controle läßt sich auf folgende Weise ausführen. Wenn die Gase mit 300°
im Kamin entweichen, so ist das Wärme-Aequivalent für Steinkohle = 6000c. Der Bedarf an Kohle ist daher für die
Erwärmung des Wassers (67447 : 6000 =) 11k,3, und für den Ofen nehmen wir vorläufig an (17852 : 6000 =) 3k,0. Nun geben 14k,3 Kohle mit ihrem absoluten
Wärme-Aequivalent = 7509 multiplicirt, die absolute Wärmemenge, welche der
Brennstoff liefert, also auch denjenigen, der mit den Verbrennungsproducten in den
Kamin abgeführt wird. Wir haben also Wärmevorrath 14,3 × 7509 = 107379c, mit denen das Wasser auf 250 – 60
= 190° zu erwärmen, der Ofentransmission und der Evacuation in den Kamin zu
genügen ist.
Die specifische Wärme der Verbrennungsproducte ist (nach Tabelle V) 14,3 ×
5,33051 = 76,2 = w.
Theilen wir nun die totale Ofenröhrenlänge in 5 gleiche Theile, so ist die
Wärmeaufnahme für jeden solchen Theil = 20,786 : 5 = 4,157 × 4,1964 = 17c,44 =
W°.
Das Wasser in den Röhren hat ursprünglich 60° und soll mit 250° den
Ofen verlassen; es wird also, indem es diese 5 Röhrenlängen durchläuft, eine
Progression stattfinden, deren erstes Glied = 60, das letzte = 250 ist, daher die
Differenz = 38. Die sich folgenden Wassertemperaturen sind also t = 60 98 136 174 212, um in der ersten Section dann
noch auf t = 250° gebracht zu werden.
Die Ofentransmission wird ebenfalls eine Progression befolgen. Wir nehmen als Summe
dieser Transmission = 17650c, die in eine
Progression von 5 Gliedern zu bringen ist; aber wir kennen weder das Anfangs-
noch das Endglied. Wir berechnen daher das erste Glied, indem wir das
Temperaturverhältniß, Initial- und Endtemperatur 1400 : 300 = 4,6 zu Hilfe
nehmen. Die Zahl n der Glieder ist 5, daher dann das
Anfangsglied = 17650 : 4,6 × 5 = 767. Es sei nun S die Summe, so finden wir die Differenz Δ der Progression durch
Textabbildung Bd. 219, S. 104
Daher ist dann die gesuchte Progression in umgekehrter
Ordnung: 6293 4911,5 3530 2148,5 767, in Summe = 17650c.
Ist nun die Initialtemperatur der Verbrennungsproducte T
= 1400°, das erste Glied der Wassertemperaturen t = 212, so ist die Absorption in der ersten Section T – t = 1400 – 212 = 1188°. Diese
mit W° = 17,44
multiplicirt = 20724c
plus Ofentransmission = 6293c. Die Summe beider = 27017c ist also verschwunden und von dem
ursprünglichen Vorrathe von 107379c in
Abzug zu bringen. Es. ergibt sich als Rest = 80362c. Daher haben die Gase nur noch die
Temperatur T = 80362 : 76,2 = 1054°.
Fährt man mit dieser Rechnung fort, so erhält man:
Wärmevorrath
T
t
T – t
Absorbtion durch
Total
Wasser
Ofen
107379
1400
212
1188 × W°=
20724
+ 6293
= 27017
80362
1054
174
880
15347
+ 4911
= 20258
60104
789
136
653
11338
+ 3530
= 14918
45186
593
98
495
8632
+ 2148
= 10780
34406
451
60
391
6819
+ 767
= 7586
––––––––––––––––––––––––
26820
352
62910
+ 17649
= 80559
Schon der Umstand, daß wir eine Temperatur von 351° statt 300° übrig
behalten, beweist, daß die Wärmeabsorption nicht ausreichend groß ist, was dann auch
die Summirung dieser beweist, denn wir haben statt 67447c nur 62922 erhalten, also um 4525 zu
wenig; diese sind noch in der Evacuationstemperatur von 351° enthalten.
Wir müssen also unsere Ofenröhren etwas verlängern. Die Ursache davon liegt darin,
daß der mittlere Werth von T – t vermöge der
Ofentransmission statt 695°, wie wir berechnet hatten, 652 geworden ist.
Versuchen wir es, die Ofenröhren um 15 Proc. länger zu nehmen, und führen dann
dieselbe Rechnung aus, so bleibt uns eine Evacuationstemperatur von nur 273°,
und wir haben einen Ueberschuß der Absorption von 1412c.
Machen wir nun den fernem Versuch, die Ofenröhrenlänge um 10 Proc. zu verlängern, so
wird W° = 22,864 × 4,1964 : 5 = 19,19 und
wir haben:
Wärmevorrath
T
t
T – t
107379
1400
212
1188 × W° =
22797
+ 6293
= 29090
78289
1027
174
853
6369
+ 4911
= 21280
57009
748
136
612
11744
+ 3530
= 15274
41735
548
98
450
8635
+ 2148
= 10783
30952
407
60
347
6659
+ 767
= 7426
––––––––––––––––––––––––
23526
309
66204
+ 17649
= 83853.
So wären wir nun so ziemlich bei der rechten Länge angelangt, da nur noch 1243 an der
Absorption fehlen. Es wird in den meisten Fällen besser sein, eher eine etwas zu
geringe als zu große Länge zu nehmen, da, wenn das Wasser und die Flamme einander
entgegenströmen, der angenommene Absorptionscoefficient eher zu klein als zu groß
ist.
Man kann sich fragen, ob es nicht zweckmäßiger wäre, eine größere Röhrenlänge in den
Ofen zu bringen, um die Temperatur der Gase auf mehr als 300° abzukühlen? Die
Ersparniß an Brennstoff würde etwa 20 Proc. sein, aber es könnte eine solche
Ersparniß nur bei Kaminhöhen von wenigstens 20m Höhe stattfinden, da der Widerstand im Ofen absichtlich etwas groß
gemacht werden muß, um die Röhren mit den Gasen in innigen Contact zu bringen.
Vielleicht wird man die Einwendung machen, daß es kaum begreiflich sei, daß die
Empirie auf eine Ofenröhrenlänge von 1/6 bis 1/5 der totalen Länge geführt habe,
während sich nun diese auf 1/15 reducirt. Diese Reduction ist jedoch vollkommen
begründet, sobald wir von der ganz unzweckmäßigen Aufwicklung der Röhren in dichte
Spiralen abgehen und denselben eine solche Lage geben, daß sie an ihrer ganzen
Peripherie vom Feuer bespült werden; denn dicht aufgewundene Röhren werden nur an
der Tangente vom Feuer berührt, so daß nur höchstens 1/6 der Peripherie als
Heizfläche wirksam sein kann. Bringen wir aber den ganzen Umfang der Röhren mit dem Feuer in Contact, so
wird der Effect erst ein vollständiger sein.
Diese ungeschickte Art, die Röhren in Spiralen aufzuwinden, erklärt auch, warum die
Empirie schon mit einer Mittlern Transmission von 100c pro 1m Röhrenlänge vorlieb nimmt. Für 317m Transmissionsröhren legen die Praktiker 63m in den Ofen und erhalten damit den Effect
1/6 × 63 = 10,5, während 22m,864 dem
Feuer blosgelegte Röhren den Effect 22,864 geben, d. i. ganz dasselbe Verhältniß wie
die Transmissionscoefficienten 100 : 212,5.
Ein nahes Zusammenlegen der Ofenröhren ist immerhin zweckmäßig, um dem Ofen nicht
eine übermäßige Größe geben zu müssen, und um die Flamme mit möglichst großer
Geschwindigkeit an der Heizfläche hinstreichen zu lassen, aber unter der Bedingung,
daß die Gase der Röhre entlang streichen, und nicht im rechten Winkel gegen
dieselben. Auch ist Gegenstrom zwischen Wasser und Feuer fast unerläßlich, da sonst
der Effect ebenfalls ein geringerer sein würde. Unser Wärmeabsorptionscoefficient
von 59c,3555 pro 1qm ist zwar der gewöhnlichen Kesselfeuerung
entnommen, bei welcher keine Gegenströmung stattfindet; dafür aber dürfen wir nicht
vergessen, daß bei Röhrenheizung ein Theil der Fläche über und nicht unter dem
Wasser ist, daher weniger wirksam. Nach Redtenbacher
verhält sich der Nutzeffect der Kesselfeuerung zu der mit Gegenstrom wie 1 : 1,35,
und wenn wir nun ferner bedenken, daß die Bewegung des Wassers indirect, nicht im
Ofen, bewirkt wird, so wird jener Coefficient nicht kleiner, noch wesentlich größer
angenommen werden können.
Um die Röhren im Ofen in thunlichster Zusammenlegung anzubringen, läßt sich ein
Kunstgriff anwenden, welcher diesem Zwecke vorzüglich entspricht. Dieser besteht
darin, das in den Ofen zurückkehrende Wasser vor dem Eintritt in denselben in zwei
oder mehrere gleich lange Röhren zu theilen und es dann beim Austritte aus dem Ofen
wieder zu vereinigen. Dies läßt sich mit Hilfe von T-Stücken leicht bewerkstelligen. Es beschreibt dann zwar das
Wasser in letztern rechte, nicht abgerundete Winkel, die doppelt so viel Widerstand
leisten als abgerundete Winkel; dafür sind dann aber die Widerstände gegen die
Circulation des Wassers im Ofen selbst geringer und zwar im Verhältnisse 5 : 4.
(Fortsetzung folgt.)
Tafeln