| Titel: | Ueber Dr. Carl Jicinsky's neuen Maaßstab; von Dr. F. Reidt. |
| Autor: | F. Reidt |
| Fundstelle: | Band 209, Jahrgang 1873, Nr. XIX., S. 121 |
| Download: | XML |
XIX.
Ueber Dr. Carl Jicinsky's neuen Maaßstab; von Dr. F. Reidt.
Mit Abbildungen auf Tab.
II.
Reidt, über den π-Meter.
Die Bemerkung in Dr. Jicinsky's Abhandlung über seinen neuen Maaßstab (den π-Meter) im polytechn. Journal Bd. CCVIII S. 25 (erstes
Aprilheft 1873) „die Verwandlung der Peripherie eines Kreises in eine
Gerade auf dem Wege geometrischer Construction sey in der Wissenschaft bisher
nur bis zu der Genauigkeit von vier Decimalen
gelungen“, ist irrig. Als ein Beispiel des Gegentheiles kann die
nachfolgende, von Jacob de Gelder, Prof. in Leyden,
herrührende Construction dienen, welche auf sechs
Decimalen richtig ist:
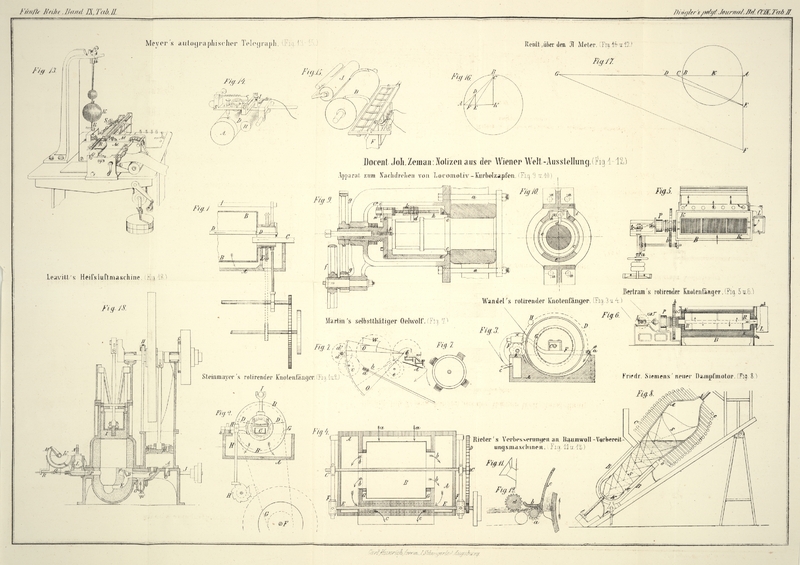
Zieht man (Fig.
16) im Kreise K zwei zu einander senkrechte
Radien KA, KB,
theilt KB in 8 gleiche Theile, verbindet den B zunächst liegenden Theilpunkt C mit A, trägt auf AC von A aus die
Strecke AD gleich der Hälfte des Radius ab, fällt
von D die Senkrechte DE auf KA, zieht CE und dann DF
parallel CE, welche Linie KA in F schneide, so
ist die halbe Peripherie gleich dem dreifachen Radius plus
AF, d.h. also für den Radius 1 ist AF = π –
3. – Es ist nämlich:
Textabbildung Bd. 209, S. 121
Eine andere derartige Construction ist folgende: Man ziehe (Fig. 17) im Kreise K einen Durchmesser AB, verlängere denselben über B hinaus und trage
auf der Verlängerung BC gleich dem fünften Theile
und CD gleich 2/5 des Radius ab, errichte in A auf AB die
Senkrechte AE gleich dem Radius, ziehe CE, verlängere AE über E und mache AF = CE, ziehe
endlich FG parallel zu DE, so ist AG
näherungsweise gleich der Peripherie. – Man findet nämlich für 75 den Näherungswerth 3,1415919,
also mit einer theoretischen Genauigkeit von fünf Decimalen.Man vergleiche über diese und ähnliche Constructionen: Reidt, Elemente der Mathematik, Bd. II, 2. Aufl. Berlin, G. Grote.
Die, übrigens recht schöne Construction des Hrn. Jicinsky
verliert an ihrer anscheinenden Einfachheit gegen die vorstehenden dadurch, daß bei
ihr auch der Winkel von 15 Grad zu construiren ist, und daß sie die Theilung des
Halbmessers in Hundertstel, ja sogar ein halbes Hundertstel des Radius verlangt, was
für die Einzel-Construction bei kleinen Radien nicht ohne Bedenken seyn wird.
Auch könnte es bei dem Beweise in wissenschaftlicher Beziehung etwas störend
erscheinen, daß ein Element aus einer dem Problem ferner liegenden, nicht rein
geometrischen Disciplin, nämlich eine trigonom. Function, benutzt wird. Dieß kann
indessen, wenn man Gewicht darauf legen will, durch die Einführung von
Textabbildung Bd. 209, S. 122
vermieden werden.
Ich habe oben die Genauigkeit solcher Näherungsconstructionen als eine theoretische hervorgehoben; in der Praxis ist die gerühmte Genauigkeit von sieben
Decimalen völlig illusorisch. Eine solche kann der
π-Meter nicht liefern. Zunächst ist
nämlich die wirkliche Ausführung der angegebenen Construction mit einer solchen
Genauigkeit, daß selbst bei einem Kreisdurchmesser gleich der Höhe des
Stephansthurmes „kein Zirkelinstrument den Fehler zwischen die Spitzen zu
fassen vermag“, absolut unmöglich; die
stets vorhandene Dicke der gezeichneten Linien, die Beschränktheit unseres
Sehvermögens, die Vergrößerung, welche z.B. ein bei dem Hundertstel des Radius noch
unmerklicher Fehler im weiteren Verlauf der Construction erleiden kann, u. dgl. m.
machen für jede nicht mehr als riesengroße Zeichnung eine Genauigkeit bis auf 7
Decimalen des Radius unmöglich; in der Praxis wird man auf construirendem Wege wohl kaum mehr als drei
Decimalen verlangen können. Eben wegen dieser unvermeidlichen Fehler des zeichnenden
Verfahrens, welche sich im weiteren Verlauf der Arbeit bis zu recht merkbaren
Fehlern des Resultates vergrößern können, zieht man ja bekanntlich überall, wo es
irgend thunlich ist, die Berechnung der gesuchten Größe
vor; denn diese ist völlig frei von jenen unvermeidlichen Fehlerquellen, läßt sich
bis zu jedem verlangten Grad der Genauigkeit durchführen, und die berechnete Größe
kann für construirende Zwecke nachher immer mit dem Maaßstab mit aller der
Genauigkeit, welche
dieser überhaupt zu bieten vermag, aufgetragen werden. – Ließe sich aber auch
die angegebene Construction mit der versprochenen Genauigkeit von sieben Decimalen
ausführen, sowie ferner der Maaßstab darnach mit derselben Genauigkeit seiner
Theilung anfertigen, so würde es doch schließlich unmöglich seyn, den angegebenen
„Strich bis zum Punkte E“ behufs Abmessung mit dem π-Meter mit solcher Genauigkeit zu ziehen,
sowie an dem damit verbundenen gewöhnlichen Maaßstab die Länge der gezeichneten
Linie mit solcher, in gewöhnlichen Fällen mehr als mikroskopischen Genauigkeit
abzulesen.
Der „π-Meter“ wird
hiernach meines Erachtens die versprochenen Leistungen auch nicht entfernt zu
liefern im Stande seyn, womit indessen der Werth desselben als praktischen
Instrumentes für eine ungefähr richtige und bequeme Zeichnung nicht bestritten
werden soll. Nur ist zu seiner Anfertigung die angegebene geometrische Construction
unwesentlich und unpraktisch; man kennt die abzutragende. Länge von π viel sicherer und bequemer durch ihren
Zahlenwerth, und der „π-Meter“ ist nichts anderes, als ein Scalenwerk,
wie man solche in ähnlicher Art schon länger für verschiedene Zwecke besitzt,Man vergl. z.B. Preßler's
Ingenieur-Meßknecht, Leipzig, Baumgärtner, wo auch das Princip des
„π-Meters“ bereits in etwas anderer Form
angewendet ist, und zwar nicht bloß für die Peripherie, sondern auch für die
praktisch wohl nicht minder wichtige Kreisfläche. um aus gewissen gegebenen Größen von ihnen abhängige, gesuchte durch
unmittelbare Ocularablesung zu ermitteln, resp. aufzutragen.
Da der Erfinder am angeführten Ort sein auf den internationalen Ausstellungen von
London und Moskau (1872) prämiirtes Werk „auch der Beurtheilung deutscher
Fachmänner“ hat unterbreiten wollen, so dürfte die vorstehende Notiz
vielleicht nicht unberechtigt seyn.
Tafeln