| Titel: | Theorie der Schwungräder für calorische Maschinen; von Rob. Röntgen. |
| Autor: | Robert Röntgen [GND] |
| Fundstelle: | Band 183, Jahrgang 1867, Nr. XX., S. 86 |
| Download: | XML |
XX.
Theorie der Schwungräder für calorische
Maschinen; von Rob.
Röntgen.
Mit Abbildungen auf Tab.
III.
Röntgen, über der Schwungräder für calorische
Maschinen.
Bei den calorischen Maschinen wird bekanntlich die Bewegung der Arbeitsmaschinen in
denjenigen Perioden, wo die treibende Kraft nicht wirkt, durch ein einseitiges
Gewicht oder Uebergewicht, welches im Ringe des Schwungrades angebracht ist,
bewerkstelligt. In der Regel und am einfachsten wird dieß dadurch erhalten, daß man
die eine Hälfte des Ringes hohl und die andere massiv gießt. Es ist im Ganzen
leicht, dieses Mehrgewicht auf der einen Seite zu berechnen, wenn man die
Widerstände, welche bei der Bewegung der Maschine entstehen, kennt. Nach den
Untersuchungen und Berechnungen des Verfassers an bestehenden calorischen Maschinen
sind diejenigen, welche beim Rückgange der beiden Kolben erzeugt, und die also
vorzüglich durch die Verdünnung und nachherige Verdichtung der eingesogenen kalten
Luft, Oeffnen der Ventile, Reibung der Kolben etc. hervorgebracht werden, so groß,
daß zu ihrer Ueberwindung dieselbe mechanische Arbeit erforderlich ist, die zur
Ueberwindung der Widerstände der Arbeitsmaschinen dient. Diejenigen Widerstände,
welche bei der umgekehrten Bewegungsrichtung der Kolben, also dann entstehen, wenn
die treibende Kraft thätig ist, mögen vielleicht stark die Hälfte der ersteren
betragen.
Da uns bis jetzt über die Größe dieser Widerstände, also auch über die Berechnung der
Uebergewichte, sowie überhaupt über die des Gesammtgewichtes des Schwungringes von
einer anderen Seite noch nichts bekannt geworden ist, so haben wir uns erlaubt, eine
derartige Berechnung, gestützt auf sorgfältige Vermessungen und Beobachtungen, an (Ericsson'schen) calorischen Maschinen in Nachstehendem mitzutheilen.
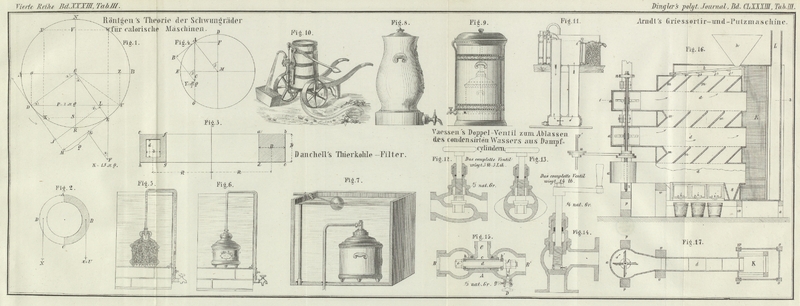
Wir bezeichnen zu dem Ende den Widerstand der Arbeitsmaschinen auf die Warze des
Krummzapfens reducirt mit Q, den Halbmesser AC = CB
Fig. 1 des
Warzenkreises mit r; das Uebergewicht des Schwungringes
mit K, die Differenz zwischen diesem und dem ganzen
Gewichte desselben mit M, und die treibende Kraft der
Lenk- oder Kurbelstange mit P. Endlich nehmen wir
an, der Halbmesser des Schwungringes sey auch = r, und
die Lenkstange behalte bei ihrer Bewegung stets eine zum Durchmesser AB des Warzenkreises parallele Richtung, oder mit
anderen Worten, die Lenkstange sey im Verhältniß zur Kurbel AC = CB sehr
lang, was für die Berechnung einfacher ist. Freilich weicht diese Annahme von der
Wirklichkeit nicht unbedeutend ab, da in der Regel die Länge der Kurbel in der der
Lenkstange circa 2 1/4mal enthalten ist, indessen
vergrößert sie nur, bei demselben Gewichte des Schwungringes, den Grad der
Ungleichförmigkeit, und zwar nach der Berechnung um das 1,3 bis 1,4fache.
Die Bewegung der Kurbel geschehe im Sinne des Pfeils. In A ist alsdann die auf Umdrehung verwendete Kraft der Lenkstange = 0, in
R erreicht sie ihr Maximum = P und in B ist dieselbe wieder = 0. Zwischen
A und R, sowie zwischen
R und B erreicht sie
also Werthe, die zwischen 0 und P liegen. Der Widerstand
der Arbeitsmaschinen ist dagegen in jedem Punkte des Warzenkreises = Q. Das Uebergewicht K setzt
der treibenden Kraft P bei seiner Hebung einen
ungleichen Widerstand entgegen. Ist die Warze des Krummzapfens in A, so befindet sich der Schwerpunkt des Uebergewichtes
in R, in diesem Falle ist offenbar sein Widerstand gegen
die Drehung der Kurbel = 0. Kommt A nach R, so rückt der Schwerpunkt von R nach B, und in diesem Falle ist der
Widerstand gegen Drehung ein Maximum, nämlich = K.
Erreicht endlich A oder die Warze des Krummzapfens den
Punkt B, so gelangt R, d. i.
der Schwerpunkt des Uebergewichtes, nach N, und dann ist
wieder der Widerstand desselben = 0. Zwischen R und B, sowie zwischen B und N ist demnach letzterer größer als 0 und kleiner als K. Sobald R den Punkt N überschritten hat, sinkt das Uebergewicht durch den
Bogen NAR herunter, wobei die Warze des
Krummzapfens den Halbkreis BNA beschreibt und
Kurbel, Lenkstange etc. wieder in ihre ursprüngliche Stellung versetzt werden.
Indem nun K durch den Bogen NAR heruntersinkt, verrichtet es offenbar die mechanische Arbeit:
K . NR = 2 rK.
Diese Arbeit muß nun der Summe der Arbeiten der Widerstände gleich seyn. Der Widerstand Q der Arbeitsmaschinen erfordert aber, indem er durch
den Bogen NAR überwunden wird, die Arbeit
πrQ,
und da die Arbeit des Widerstandes, der durch die Reibung der
Kolben, Compression der kalten Luft etc. entsteht, 2mal so groß ist, so haben
wir:
2rK
= πrQ + 2 πrQ = 3 . πrQ,
also K
= 1,5 πQ = 4,712 Q
(I)
Da wir nun aus der Zahl der Pferdestärken, dem Halbmesser r des Warzenkreises oder des Schwungringes und der
Umdrehungsgeschwindigkeit desselben, Q leicht berechnen
können, so ist damit auch sofort K bestimmt.
Untersuchen wir nun, wie groß die Leistung der Kraft P
seyn muß. Dieselbe hat 1) den Widerstand Q der
Arbeitsmaschinen durch den Weg πr und dann
2) den des Uebergewichtes K durch den Weg 2 r zu überwinden. Da nun die mechanische Arbeit von P für jede Kurbelumdrehung 2 rP ist, so hat man:
2 rP = πrQ + 2 rK,
oder wenn man für K den Werth aus
(I) setzt:
2 rP = πrQ + 3 . πrQ = 4 . πrQ,
daher
P = 2 πQ =
6,2832 . Q
(II)
Steht nun die Warze des Krummzapfens in A, so ist die
drehende Kraft von P = 0, der Widerstand aber = Q Kommt A nach R, so ist die drehende Kraft = 2 πQ = 6,2832. Q.
Da in diesem Falle der Schwerpunkt von K nach B gekommen ist, so widersteht K der drehenden Bewegung mit seinem vollen Gewichte, d.h. mit K oder mit 4,712 Q; außerdem
beträgt auch hier der Widerstand der Arbeitsmaschinen Q,
so daß der Gesammtwiderstand = 5,712 Q ist. Es
überbietet demnach die drehende Kraft P den Widerstand
um 6,2832 Q – 5,712 Q. Zwischen A und R
muß es demnach einen Punkt geben, wo die drehende Kraft von P der entgegenwirkenden drehenden Kraft von K
und dem Widerstande Q der Arbeitsmaschinen das
Gleichgewicht hält. Es möge D dieser Punkt seyn und α der Winkel, den alsdann die Kurbel mit dem
Durchmesser AB bildet. Ist aber die Warze der
Kurbel in D, so ist der Schwerpunkt des Uebergewichtes
in E, welcher Punkt ebensoweit von R absteht als D von A. Und denkt man sich C mit
E verbunden, so muß < ECR = α seyn.
Bezeichnet nun die Linie EF das Gewicht von K, so ist die daraus resultirende Kraft EG, welche der drehenden Bewegung der Kurbel
widersteht, wie leicht erhellt:
EG = EF . sin α =
K. sin α = 1,5 πQ sin α.
Drückt nun die Linie GH noch den Widerstand Q der Arbeitsmaschinen aus, so ist die widerstehende
drehende Kraft = EH
= Q + 1,5 πQ sin α = Q (1 + 1,5 π sin α).
Die drehende Kraft von P im Punkte D möge DJ seyn, alsdann muß offenbar DJ = EH genommen
werden. Aber
DJ = P sin α =
2 . πQ sin α.
Wir haben also:
2 . πQ
sin α = Q (1 + 1,5
π sin α)
2 π sin α = 1 + 1,5 π sin α
0,5 π sin α = 1
sin
α = 1/0,5 . 3,1416 = 0,6366,
daher α = 39° 32',3 = 39,538°.
In dem Punkte U, der von B um
den Bogen α = 39,538° absteht, muß wieder
die drehende Kraft von P den Widerständen das
Gleichgewicht halten. Ist aber die Warze des Krummzapfens von D nach U gekommen, so hat der Schwerpunkt des
Uebergewichtes die Höhe EW zurückgelegt. Auf dem
Wege DU muß nun offenbar die mechanische Arbeit
von P größer, dagegen auf den Strecken AO und ZB
kleiner seyn als die des Gesammtwiderstandes. Das „Mehr“ der
mechanischen Arbeit von P auf dem Wege DU wird daher auf die Beschleunigung der Massen,
insbesondere also auf die Beschleunigung des Schwungringes sammt Uebergewicht (M + K) verwandt. Umgekehrt
wird diese Beschleunigung, wenn P die Strecken AO und ZB
durchläuft, wieder zugesetzt. – Wir erhalten demnach die Arbeit, welche jene
Beschleunigung in Anspruch nimmt, wenn wir von der Arbeit der Kraft P auf dem Wege DU
diejenige abziehen, welche die Hebung von K auf die Höhe
EW und der Widerstand Q bei Durchlaufung des Bogens DRU
erfordert.
Die Arbeit von P auf dem Wege DU beträgt:
DU . P = 2 . CO . P = 2 . r cos αP
= 2 r cos α . 2 πQ = 4 cos απrQ.
Der Widerstand Q erfordert, indem er durch den Bogen DRU überwunden wird, die Arbeit:
Q . Bogen DRU
Aber Bogen DRU ergibt sich aus der Proportion: 180
: 180 – 2α = πr : x, woraus x = (180 – 2α)/180 πr = (90 – α)/90 πr ist. Demnach hat
man:
Q . Bogen DRU = (90
– α)/90 πrQ
Da K auf die Höhe EW
gehoben wird, so ist hierzu die mechanische Arbeit:
K . EW = 2 . CS . K = 2 . r cos α . K = 2 r cos α 1,5 πQ = 3 cos
απrQ nothwendig.
Bezeichnet v₀ die Geschwindigkeit, welche der Schwungring und das Uebergewicht
besitzen, wenn die Warze der Kurbel in D steht, v₁ aber diejenige, wenn die Warze den Punkt U erreicht hat, so beträgt die hierzu verwendete
Arbeit:
(M + K)/2g (v₁² – v₀²).
Wir haben demnach folgende Gleichung:
4 cos απrQ
= (90 – α)/90 πrQ + 3 cos απrQ
+ (M + K)/2g (v₁²
– v₀²).
Also:
(M + K)/2g (v₁²
– v₀²)
= cos
απrQ – (90 –
α)/90 πrQ
= (cos α – (90 – α)/90) πrQ
= (0,7712–0,5607) πrQ
= 0,2105 πrQ
oder endlich
(M + K)/2g (v₁² – v₀²) =
0,6613 rQ (III)
Ist nun v die mittlere Warzengeschwindigkeit bei jeder
Umdrehung, 1/n der Grad der Ungleichförmigkeit, so hat
man bekanntlich:
(v₁ + v₀)/2 = v
oder v₁ + v₀ = 2v
und v₁ + v₀ = 1/nv,
daher v₁² – v₀² = 2/n
v² (IV)
Wird dieser Werth oben substituirt, so entsteht:
(M + K)/2g . 2/nv² = 0,6613 rQ
oder 1/n
v² (M + K) = 31 1/4 . 0,6613 rQ = 20,66567 r
Q (V)
Ist also 1/n und v bekannt,
so hat man:
M + K = 20,6656 rQn/v²,
und setzt man M + K und v als bekannt voraus,
so ergibt sich:
1/n = 20,6656rQ/(M + K)v².
Den Werth von Q kann man nun leicht berechnen. Die Kurbel
mache pro Minute u
Umdrehungen und N sey die Anzahl der Pferdestärken,
welche die Arbeitsmaschinen zu ihrem Betriebe erfordern, alsdann muß
v = 2πru/60 = πru/30 = 0,1047 ru (VI)
seyn. Multiplicirt man aber die Geschwindigkeit v der Warze des Krummzapfens mit dem Widerstande Q daselbst, so erhält man die Leistung pro Secunde, also N
Pferdestärken oder 480. N preuß. Fußpfund, da eine
Pferdestärke in Preußen 480 Fußpfund beträgt. Wir haben demnach:
vQ = 0,1047 ruQ
= 480 N,
mithin:
Q = 480/0,1047. N/ru = 4584 N/ru (VII)
Wird dieser Werth in (V) eingesetzt, so entsteht:
1/n v²(M + K) = 20,6656 . r . 4584 N/ru =
94705 N/u.
Es ist also:
M + K = 94705 Nn/uv² (VIII)
oder
(M + K)
v² = 94705 N
n/u.
Wir haben hierbei angenommen, daß der mittlere Halbmesser des Schwungringes r sey, daß also auch der Schwerpunkt von K den Abstand r von der
Drehachse C besitze. Ist dagegen der mittlere Halbmesser
des Schwungringes = R, also auch der Abstand jenes
Schwerpunktes von C = R, ist
ferner für diesen Fall das Uebergewicht = U, das übrige
Gewicht des Schwungringes = G, die mittlere
Geschwindigkeit desselben = c, so muß bei gleicher
lebendiger Kraft beider Schwungringe
(M + K)
v² = (G + U) c²
seyn, d.h. das eine Product muß durch das andere ersetzt
werden können Wir haben also auch:
(G + U)
c² = 94705 Nn/u
oder
G + U = 94705 Nn/uc² (IX)
Beispiel 1.
Es sey N = 1, die Zahl der Umdrehungen pro Minute (u) = 44, der
mittlere Halbmesser (R) des Schwungringes 2,282 Fuß und
der Grad der Ungleichförmigkeit (1/n) werde zu 1/30
angenommen, n sey also = 30; wie groß ist G + U und U?
Setzt man in (VI) R statt r,
so geht v in c über; es ist
also:
c = 0,1047 Ru = 0,1047
. 2,282 . 44 =10,512 Fuß,mithin c² = 10,512
. 10,512 = 110,502.
Aus (IX) ist also:
G + U = 94705 (1 . 30)/(44 .
110,5) = 2841150/4862 = 583 Pfd.
Wird in (VII) R statt r
gesetzt, so entsteht:
Q = 4584 N/Ru = 4584 1/2,282 . 44 = 4584/100,4 = 45,7 Pfd.
beinahe.
Nun ist nach (I) K oder U =
4,712 Q, daher
K = 4,712 . 45,7 = 215 Pfd.
Bei einer calorischen Maschine, welche besonders zum Abdrehen von Messing bestimmt
war und bei der N, u und R
die oben angegebenen Werthe besaß, betrug nach den sorgfältigen Vermessungen und
Berechnungen des Verfassers U = 210 bis 220 Pfd., und
G etwa 361 Pfd., mithin U + G = 571 bis 581 Pfd. Wir glauben, daß
diese Angaben nicht um 10 bis 15 Pfd. von der Wahrheit abweichen.
Uebrigens wird bei diesem Gewichte, da die Lenkstange nicht sehr vielmal länger ist
als die Kurbel, der Grad der Ungleichförmigkeit größer seyn als 1/30. Er wird bei
dem gewöhnlichen Verhältniß zwischen Länge der Kurbel und Lenkstange 1 : 2 1/8 bis 1
: 2 1/4 etwa 1,4mal so viel betragen, d. i. 1,4 . 1/30 = 14/300 = 1/21 bis 1/22.
Dieß ist auch für die meisten Zwecke, zu welchen calorische Maschinen angewandt
werden, durchaus hinreichend.
Beispiel 2.
Für eine zweipferdige calorische Maschine sey R = 37 Zoll
= 3,083 Fuß, u = 38 und 1/n werde zu 1/30
angenommen, wie groß ist U und G + U?
Nach Formel (VII) ist, wenn man R statt r setzt:
Q = 4584 2/(3,083 . 38) = 78,3.
Aus (I) ist:
K = 4,712 . Q = 4,712 . 78,3
= 369 Pfd.
Für G + U hat man:
G + U = 94705 (2 . 30)/(38 .
c²),
c aber ergibt sich aus (VI):
c = 0,1047. 3,083. 38 = 122,65 Fuß,
daher:
G + U = 94705 (2 .
30)/(38 . 122,65) = 1219 Pfd.
––––––––––
Hiernach werden wir nun auch mit Leichtigkeit das Gewicht der schwereren und
leichteren Seite des Schwungringes bestimmen können. Es sey Fig. 2, ABC die schwerere und ADC die leichtere Seite desselben, B der
Schwerpunkt der einen und D der anderen. Wiegt die
leichtere Seite x Pfd., so wiegt die schwerere x + U Pfd. Daher haben
wir:
x + x + U
= G + U
2x
= G
x
= G/2
und x + U
= G/2 + U
Für unser 1. Beispiel ist:
2x + 215
= 583
2x
= 368
x
= 184 Gewicht der leichteren Seite.
x + U
= 184 + 215 = 399 Pfd. Gewicht der schwereren Seite.
Nunmehr können wir auch die Dimensionen des Schwungringes berechnen.
Es sey abcd, Fig. 3, der Querschnitt
der gefüllten oder schwereren, efgh der der hohlen
oder leichteren Hälfte des Schwungringes. R sey der
mittlere Halbmesser beider Hälften in Zollen, B sey die
Breite und D die Dicke des Ringes, b und d möge die Breite und Tiefe der Höhlung in der
leichteren Hälfte, Alles in Zollen gegeben, bezeichnen.
Der kubische Inhalt der gefüllten Hälfte beträgt alsdann
πRBD Kubikzoll = (π. RBD)/1728 =
0,00182 RBD Kubikfuß,
1 Kubikf. Gußeisen wiegt circa 460 Pfd., mithin 0,00182
RBD Kubikfuß:
460 . 0,00182 RBD = 0,837 RBD Pfd.
(X)
Dieß ist das Gewicht der schwereren Hälfte und = x + U
Der kubische Inhalt der Höhlung beträgt:
πRbd Kubikzoll = (πRbd)/1728 = 0,00182 Rbd
Kbkf.
Dieser Raum gefüllt gedacht, liefert das Uebergewicht auf der anderen Seite. Das
Gewicht hiervon beträgt:
460 . 0,00182 Rbd =0,837 Rbd
Pfd. (XI)
und dieß muß = U seyn.
Sobald also R, B und b als
bekannt vorausgesetzt werden, lassen sich D und d aus beiden Gleichungen bestimmen.
Bei der einpferdekräftigen calorischen Maschine war R =
2,282 Fuß = 27,384 Zoll, B = 3,75, b =2,917 Zoll, x + U = 399 und U = 215 Pfd.,
wie groß ist D und d?
Nach Gleichung (X) ist:
0,837 . 27,384 . 3,75 . D = 399
D = 399/(0,837 . 27,384 . 3,75) = 4,6 Zoll.
Aus (XI) hat man:
0,837 . 27,384 . 2,917 . d = 215
d = 215/(0,837 . 27,384 . 2,917)= 3,2 Zoll.
Untersuchen wir nunmehr noch, ob auch wirklich der Mangel an mechanischer Arbeit von
Seiten der Kraft P auf den Strecken AO und ZB, Fig. 1, jenem
Ueberschusse auf dem Wege DU gleich ist. In diesem
Falle müssen wir das Gewicht des Schwungringes auch aus diesem Mangel an Arbeit
berechnen können.
Indem also der Schwungring die Bogen UB und AD durchläuft, muß er seine auf dem Bogen DRU empfangene lebendige Kraft wieder abgeben und
seine Geschwindigkeit v₁, die er in U besitzt, muß in D wieder =
v₀ seyn. Denn auf dem Wege BNA kann er Nichts an lebendiger Kraft verlieren,
weil nach unserer Annahme die mechanische Arbeit des Uebergewichtes K, wenn der Schwungring jenen Bogen durchläuft, dieselbe mechanische
Arbeit leistet, welche die Gesammtwiderstände erfordern. Wenn wir also zu der
mechanischen Arbeit von P auf den Wegen ZB und AO noch
die aufgenommene lebendige Kraft des Schwungringes (M +
K)/2g (v₁² – v₀²) legen, so müssen wir die Arbeit erhalten, welche der
Widerstand Q der Arbeitsmaschinen auf den Bogen UB und AD und
die Hebung des Gewichtes K durch die Höhen VN und RS
erfordert.
Die Arbeit von P auf den Wegen AO und ZB
beträgt, da diese Strecken offenbar gleich groß sind:
2 (r – r cos α) P = 2r (1 – cos α) 2 π Q.
Die Arbeit, welche K erfordert, um durch die Wege VN. RS gehoben
zu werden, ist
2 (r – r cos α) K = 2r (1 – cos α) 1,5 π Q.
Für die Arbeit des Widerstandes Q durch die gleichen
Bogen UB und AD
haben wir:
α/90 πrQ
denn es verhält sich:
180 : 2 α = π r : x,
woraus x = 2 α/180 π r = α/90 πr
ist.
Hiernach können wir folgende Gleichung bilden:
(1 – cos α) 4 πrQ + (M + K)/2g (v₁² – v₀²) = (1 – cos α) 3
π Q + α/90
πrQ
oder:
(M + K)/2g (v₁² – v₀²)
= (1 – cos α) 3 π Q + α /90 πrQ
= (α/90 – (1 – cos α)) π r
Q
= (0,4393 – 0,2288) π r Q
= 0,2105 πrQ
oder
(M + K)/2g (v₁² – v₀²) =
0,6613 rQ.
Mithin derselbe Werth, den wir unter (III) gefunden haben.
Untersuchen wir noch, ob die Bewegungsverhältnisse beim Sinken des Uebergewichtes
dieselben sind, wie beim Steigen. Wir müssen uns hier K
in zwei Theile zerlegt denken, von welchem der eine, etwa X, beim Sinken dieselbe Arbeit leistet, welche die Widerstände der
Kraftmaschine, vor Allem also die Reibung der beiden Kolben (Arbeits- und Speisekolben), die
Verdünnung und Verdichtung der kalten Luft etc. erfordern, und der andere Y die Arbeit der Arbeitsmaschinen vollführt. Denken wir
uns die ersteren Widerstände auf die Lenkstange reducirt, so erfordern sie zu ihrer
Ueberwindung die Arbeit 2 r
Q₁, wenn wir dieselben mit Q₁, bezeichnen; dieselbe Arbeit verrichtet aber auch X beim Sinken von der Höhe 2r; es muß demnach X dem Q₁, in allen Punkten seiner Bahn das
Gleichgewicht halten. Der andere Theil Y hat beim
Niedergehen die Arbeit des Widerstandes Q₁ der
Arbeitsmaschinen zu leisten. Demnach muß
2rY = πrQ
oder Y = π/2 Q
seyn.
Es sey nun A, Fig. 4, derjenige Punkt,
in welchem die drehende Kraft AB von Y dem Widerstande Q gleich
ist, alsdann muß offenbar
Y sin β = AB =
Q
oder π/2 Q sin β = Q
sin β = 2/π
0,6366
und < β =
39,538° seyn.
Denselben Werth haben wir auch in Fig. 1 für < α gefunden.
Die Arbeit von Y, indem dieser Theil von K durch die Sehne AG
sinkt, beträgt:
2 . FM . Y
= 2 r cos α Y = 2 r cos α π/2 Q
= cos α
πrQ
Der Widerstand Q legt dabei den Bogen AEG zurück. Dieser ist
(180 : 180 – 2 α = π r : x) = (90
– α)/90 π
r,
also die Arbeit von Q:
(90 – α)/90 πrQ.
Hat nun der Schwungring, wenn der Schwerpunkt des Uebergewichtes in A ist, die Geschwindigkeit w₀, hat er, wenn dieser Punkt nach G
gekommen ist, die Geschwindigkeit w₁, so ist die
vom Schwungringe aufgenommene Arbeit:
(M + K)/2g (w₁² – w₀²).
Wir haben demnach:
cos α πrQ
= (90 – α)/90 πrQ + (M + K)/2g (w₁² – w₀²)
oder
(M + K)/2g (w₁² – w₀²) =
(cos α – (90 – α)/90) π r
Q.
Denselben Werth fanden wir für (M + K)/2g (v₁² – v₀²); woraus wir ersehen, daß w₁² – w₀² = v₁² – v₀² ist. Da aber v₁²
– v₀² = 2/n
v² war, so muß auch w₁²
– w₀² = 2/n
v², d.h. w₁ – w₀ muß = 1/nv seyn,
oder der Grad der Ungleichförmigkeit muß beim Sinken des Uebergewichtes derselbe
seyn, wie beim Steigen.
Die Geschwindigkeiten, welche der Schwungring besitzt, wenn sich der Schwerpunkt des
Uebergewichtes in B, W, N, X und X₁ Fig. 1 befindet, lassen sich leicht ermitteln.
Da der Schwungring auf dem Wege oder Bogen UB die
halbe lebendige Kraft abgibt, die er auf dem Wege DRU empfangen hat, so muß, wenn wir die Geschwindigkeit, die der
Schwerpunkt des Uebergewichtes in N besitzt, mit w bezeichnen:
(M + K)/2g (v₁² – w²) = 0,33065
Q
seyn. Seite 94.
Mithin
(M + K)
(v₁² – w²) = 20,6656 rQ,
oder (M + K) w² = (M
+ K) v₁²
– 20,6656 rQ (1)
Kommt der Schwerpunkt von N nach X, und ist in X seine Geschwindigkeit = w₀, so ergibt sich, wie eine einfache Betrachtung
zeigt, w₀ aus der Gleichung:
(M + K)/2g (w²
– w₀²) = 1/2 ( α/90 – (1 – cos α)) πrQ,
oder
(M + K)
(w² – w₀²) = 20,6656 rQ
(M + K)
w₀² = (M +
K) w² –
20,6656 rQ
Und wenn man für (M + K) w² den Werth aus (1) setzt:
(M + K)
w₀² = (M +
K) v₁²
– 41,3312 rQ
(2)
Gelangt der Schwerpunkt nach X₁, so ist seine
Geschwindigkeit bekanntlich = w₁ und man hat
hierfür
(M + K)/2g (w₁² – w₀²) = (
cos α – (90 – α)/90) πrQ = 0,66137 rQ
(M + K)
(w₁² – w₀²) = 41,3312 rQ
(M + K)
w₁² = (M +
K) w₀² +
41,3312 rQ.
Und setzt man für (M + K) w₀² den Werth aus (2), so entsteht:
(M + K)
w₁² = (M +
K) v₁²
(3)
Indem der Schwerpunkt von X₁ bis R sinkt, gewinnt der Schwungring das an Geschwindigkeit,
was er auf dem Wege NX verloren hat. Ist demnach
die Geschwindigkeit in R = x, so muß seyn:
(M + K)/2g (w₁² – x²) = 0,33065
rQ
oder
(M + K)
(w₁² – x²) = 20,6656 rQ
(M + K)
x² = (M + K) w₁²
– 20,6656 rQ.
Substituirt man für (M + K)
w₁² den Werth aus voriger Gleichung,
so entsteht:
(M + K)
x² = (M + K) v₁²
– 20,6656 rQ (4)
Ebenso findet man für die Geschwindigkeit y, welche der
Ring besitzt, wenn der Schwerpunkt nach E gelangt:
(M + K)
y² = (M + K) v₁²
– 41,3312 rQ (5)
Denselben Werth findet man auch für v₀, wenn man
dieß aus der Gleichung
(M + K)/2g (v₁² – v₀²) =
0,6613 rQ (Seite 89)
entwickelt.
Aus diesen Darstellungen folgt:
1) der Schwerpunkt hat in N und R gleiche Geschwindigkeit w oder x;
2) sind die Geschwindigkeiten in X
und E gleich, nämlich w₀ = v₀ oder y;
3) sind dieselben in X₁ und
W gleich, w₁
= v₁.
Kennt man nun v₁, so ist dadurch auch w, w₀ etc. bestimmt.
Zur Entwickelung von v₁ aber dienen die
Gleichungen:
v₁ + v₀ = 2v
und v₁ – v₀ = 1/n v,
woraus man hat:
2 v₁ = (2 + 1/n) v
und v₁ = 1/2 (2 + 1/n) v
Es ist daher
v₁² = 1/4 (4 + 4 . 1/n + (1/n)²) v²
Oder, wenn man (1/n)² gegen 4 . 1/n als sehr klein vernachlässigt:
v₁² = 1/4 (4 + 4 . 1/n) v² = (1 + 1/n) v².
Setzen wir dieß in die Gleichungen (1), (2), (3) etc. ein, so entsteht:
(M + K)
w² = (M + K) (1 + 1/n) v² – 20,6656 rQ.
Mithin:
Textabbildung Bd. 183, S. 98
Ferner:
(M + K)
w₀² = (M +
K) (1 + 1/n) v² – 41,3312 rQ,
oder
Textabbildung Bd. 183, S. 98
Endlich:
w₁ = v₁ =
√(1 + 1/n)v² =
v √(1 + 1/n) (C)
Anmerkung. Da v die
Geschwindigkeit des Schwungringes für den Halbmesser r,
c dagegen die für den Radius R bezeichnet, so
darf man auch c statt v
setzen, wenn man nur statt r, R in die Rechnung
einführt.
Beispiel 3.
Für die einpferdekräftige calorische Maschine war R =
2,282 und c = 10,512 Fuß, Q
betrug 45,7 und M + K oder
G + U = 583 Pfd.;
endlich war 1/n = 1/30; wie groß ist v₁ oder w₁,
v₀ oder w₀ und w oder x?
Es ist nach (C)
v₁ = w₁
= 10,512 √(1+ 1/30) = (10,512√390)/30
= 10,512 . 30,496/30 = 10,6858 Fuß.
Für v₀ oder w₀
haben wir, nach (B)
Textabbildung Bd. 183, S. 99
Endlich ist w oder x nach
(A)
Textabbildung Bd. 183, S. 99
d. i. sehr nahe die mittlere Geschwindigkeit v.
Es läßt sich auch allgemein beweisen, daß die Geschwindigkeit, welche die Warze des
Krummzapfens in A und B oder
der Schwerpunkt des Uebergewichtes in R und N besitzt, also die Geschwindigkeiten w oder x der mittleren
Geschwindigkeit v sehr nahe gleich sey.
Aus (1) ist:
(M + K)
v₁² = (M +
K) w² + 20,6656
rQ
und wenn man statt v₁² den obigen Werth setzt:
(M + K)
(1 + 1/n) v² = (M + K) w² + 20,6656 rQ.
Nach Gleichung (V) ist aber:
(M + K)
v² = 20,6656 nrQ (α)
Daher:
20,6656 nrQ (1 + 1/n) = (M + K) w² + 20,6656 rQ
oder
(M + K)
w² = 20,6656 r Q
(n + 1 – 1) = 20,6656 nrQ (β)
Aus (α) und (β)
folgt:
(M + K)
v² = (M + K) w²
d.h. v = w = x,
sehr nahe, weil eigentlich v₁² = 1/4 (4 + 4n + (1/n)²)v² war,
und also 1/4 . (1/n)² vernachlässigt worden
ist.
Ermitteln wir schließlich noch den Wirkungsgrad der (Ericsson'schen) calorischen Maschinen.
Wir nehmen an, daß die mechanische Arbeit, welche durch die Reibung der beiden Kolben
etc., wenn dieselben von der expandirten heißen Luft bewegt werden, in Anspruch
genommen wird, für jede Kurbelumdrehung der Hälfte der Arbeit gleich sey, welche die
Arbeitsmaschinen erfordern, also = πrQ sey.
Da die auf die Lenkstange übertragene Arbeit pro
Kurbelumdrehung 4 πrQ beträgt, so würde die
Totalleistung der Maschine = 5 πrQ
betragen. Hiervon wird nur 2 πrQ zur
Bewegung der Arbeitsmaschinen nützlich verwandt, woraus man also den Wirkungsgrad:
(2 πrQ)/(5 πrQ) = 0,4
also nur 40 Procent der Totalleistung erhält. Vielleicht ist
diese Zahl noch eher etwas zu hoch als zu niedrig.
Remscheid, im December 1866.
Tafeln