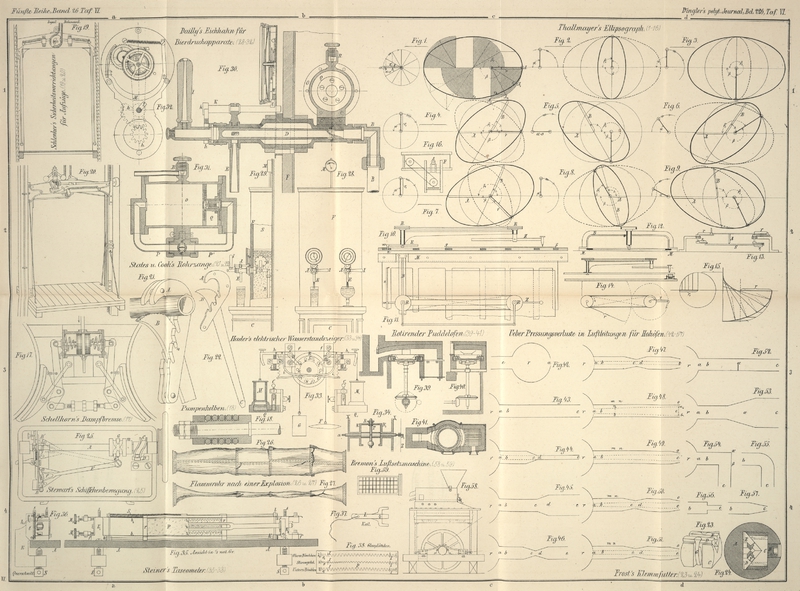
| Titel: | Ellipsograph von Prof. V. Thallmayer in Ungarisch-Altenburg. |
| Autor: | V. Thallmayer |
| Fundstelle: | Band 226, Jahrgang 1877, S. 238 |
| Download: | XML |
Ellipsograph von Prof.
V.
Thallmayer in Ungarisch-Altenburg.
Mit Abbildungen aus Taf. VI [c.d/1].
Thallmayer's Ellipsograph.
Nachfolgend erlaube ich mir, angeregt durch Delabar's Aufsatz über Ellipsographen (1877 * 223 461. 224
374), einen von mir entworfenen Apparat bekannt zu machen, der
wohl nicht die Bestimmung hat, Ellipsen auf dem Reißbrete zu
verzeichnen, welcher aber vermöge seiner Einfachheit und
leichten Einstellbarkeit ganz gut verwendet werden kann, wenn
auf Holz-, Blech- oder sonstigen Tafeln behufs Aussägen,
Ausstanzen, Bemalen u. dgl. zu gegebenen Halbachsen, oder auch
zu gegebenen conjugirten Durchmessern Ellipsen verzeichnet
werden sollen. Der Apparat kann wohl auch Ellipsenzirkel genannt
werden, indem ein Stangenzirkel während seiner Drehung auf einer
unter ihm hin- und hergleitenden Fläche die Ellipse
beschreibt.
Mit einem solchen Ellipsographen, obwohl er nur aus der Hand
eines mit den einfachsten Werkzeugen arbeitenden Drechslers
hervorging, somit bei weitem nicht jene Vollkommenheit der
Ausführung besaß, mit welcher ihn ein Maschinenbauer oder
Mechaniker ausgestattet hätte, habe ich sowohl mit Bleistift,
als auch mit Reißfeder und Pinsel über Erwarten reine und scharf
ausgezogene Ellipsen verzeichnet; dabei waren weder Bleistift
noch Reißfeder mit den sonst bei regelrechter Ausführung
angewendeten Spiralfedern versehen. Es ist anzunehmen, daß
dieser Apparat, wenn statt des Stiftes
entsprechend geformte Einsatzspitzen zur Verwendung kommen, zur
Herstellung von elliptischen Formen in weichem Material (Thon,
Gyps, Formsand) geeignet sein dürfte.
Der Ellipsograph (Fig. 10
bis 12)
besteht aus einem die Zirkelschiene Z und die Kurbelschiene K
aufnehmenden Bügel B, welcher in
einen horizontalen Arm ausläuft und auf den Führungsschienen M festgemacht ist. Zwischen den
Führungsschienen befindet sich der Schlitten S, in dessen auf die Führungsrichtung
senkrechtem Schlitze n die Warze w der Kurbelschiene einspielt, und
welcher die Tafel, auf der die Ellipse verzeichnet werden soll,
aufnimmt. Zirkel- und Kurbelschiene lassen sich in den
zugehörigen Verticalzapfen verschieben und können mit einer
Klemmschraube in der gewünschten Einstellung festgehalten
werden. Die erwähnten zwei Verticalzapfen werden durch zwei
Scheiben R von gleich großem
Durchmesser und durch eine auf sie entweder offen oder gekreuzt
aufgelegte Schnur in Umdrehung versetzt, so daß nothwendiger
Weise gleichzeitig die Drehung des Zirkels und die geradlinige
Bewegung des Schlittens eintreten muß. Will man von der
Anwendung einer Schnur oder eines Riemens behufs Bewegung des
Zirkels Umgang nehmen, so kann man statt ihrer auch zwei mit
einer Schiene verbundene Kurbeln von gleicher Armlänge
verwenden, wie dies in Figur 11
angedeutet ist.
Die Lage und Form der vom Zirkel beschriebenen Ellipse hängt
einestheils ab von der zur Wirkung kommenden Kurbelschienenlänge
r₁ und Zirkelschienenlänge
r (Fig. 14);
anderntheils aber haben auf Lage und Form der Ellipse auch
Einfluß der Winkel, unter welchem die zwei Schienen anfänglich
eingestellt wurden, und der Umstand, ob eine offen oder gekreuzt
aufgelegte Schnur verwendet wird. Die Einstellung auf ein
gegebenes r und r₁ geschieht einfach durch
Verschieben der betreffenden Schienen in ihren Verticalzapfen;
der Schlitten ist hierbei nicht hinderlich, indem auch er beim
Verschieben der Kurbelschiene in den Führungsbacken sich
verrückt. Es können Zirkel- und Kurbelschiene leicht so
angebracht werden, daß man mit r und
r₁ auf beliebig kleine
Einstellungen herabgehen kann.
Die Figuren 1
bis 10
bringen Ellipsen zur Ansicht, wie sie bei den angedeuteten
Anfangsstellungen von r₁ und
r beschrieben werden, und zwar
resultiren die voll ausgezogenen Ellipsen bei Anwendung einer
offenen, die punktirt gezeichneten hingegen bei Anwendung einer
gekreuzten Schnur. Wo keine punktirt gezeichnete Ellipse
vorhanden ist, bringen sowohl offene, als auch gekreuzte Schnur
eine und dieselbe Ellipse zu Stande. Für gewöhnlich wird man, da
es nicht häufig vorkommen dürfte, gegebenen conjugirten
Durchmessern entsprechende Ellipsen verzeichnen zu müssen,
selten andere als die den Figuren 1
bis 3
entsprechenden Einstellungen anzuwenden haben. Diese
Einstellungen geben Ellipsen, deren Halbachsen beziehungsweise
r + r₁, und r, sowie r – r₁ und r sind.
Der die Entstehung der Ellipse in Figur 1
veranlassende Vorgang in den Bewegungsverhältnissen ist von
Viertel zu Viertel fortschreitend dargestellt. Steht nämlich bei
Anwendung einer offenen Schnur der Stift bei A und die Kurbelwarze bei a, so wird nach einer Drehung um den
Winkel γ jeder Punkt der
Schlittenfläche um das Stück r₁ , (1 – cos γ) nach vorwärts verschoben;
es kann also der Stift nicht auf den Punkt A₁ treffen, auf den er treffen
müßte, wenn die Schlittenfläche unbeweglich wäre, sondern er
wird auf einen Punkt c₁
treffen, der um das Stück r₁
(1 – cos γ) vor dem
Punkte A₁ liegt. Aehnliches
gilt auch bezüglich der Punkte A₂, A₃, so daß
vom Stifte statt der durch Schraffirung angedeuteten
Viertelkreise Viertelellipsen beschrieben werden, was leicht
nachgewiesen werden kann; speciell Figur 1
betreffend, kann auf das bekannte und dort auch angedeutete
Verfahren, eine Ellipse aus den zwei über ihre große und kleine
Halbachse beschriebenen Kreisen zu construiren, hingewiesen
werden.
Bezeichnet man mit α den
Winkel, um welchen die Schiene r₁ von der Führungsrichtung des Schlittens absteht,
mit β hingegen den im Sinne
der Umdrehungsrichtung der Zirkelschiene gemessenen Winkel, den
diese Schiene mit der Führungsrichtung des Schlittens
einschließt, so findet man, wenn A
und B die Hälften eines Paares
conjugirter Durchmesser sind, von denen A mit, der Führungsrichtung zusammenfällt:
Textabbildung Bd. 226, S. 239
und für den Winkel Δ, den diese zwei conjugirten Durchmesser
einschließen,
Textabbildung Bd. 226, S. 239
Bezeichnet man ferner der Kürze halber den
Ausdruck
Textabbildung Bd. 226, S. 239
mit M und de
Ausdruck [r – r₁ cos (α + β)]² r₂ mit N, so ergibt sich zur Bestimmung der zwei Halbachsen der
Ellipse:
Textabbildung Bd. 226, S. 239
und
Textabbildung Bd. 226, S. 239
Aus diesen Gleichungen ergeben sich die
betreffenden Werthe für specielle Annahmen durch Substitution.
Bei Verwendung einer offenen Schnur kann, wenn der Winkel, den
die zwei Halbmesser r und r₁ mit einander einschließen, mit
φ bezeichnet wird, statt α + β der während der Drehung constant bleibende Winkel
φ benutzt werden.
Zieht man, wie in Figur 15,
von den einzelnen Punkten der Ellipse die Richtungen, welche der
Zirkelschiene in den betreffenden Punkten zukommen, so läßt sich
nachweisen, daß die zwischen den zwei Halbachsen liegenden
Stücke dieser Richtungslinien constant und dem Unterschiede der
beiden Halbachsen gleich sind; somit kann man sagen, daß bei
diesem Ellipsographen die Kreuzführung der ältern Ellipsographen
durch den Schlitz und die Kurbelschiene ersetzt ist. In Figur 15 sind auch die Abweichungen der Richtungen der
Zirkelschiene von den Normalen zu den betreffenden Punkten
angedeutet.
Zum Schlusse noch einige Bemerkungen. Sind die zwei Scheiben R ungleich groß, so erhält man von der
Ellipse abweichende Curven, die aber mehr interessant als
praktisch wichtig sind. Wird die Unterlagsfläche S von zwei Kurbeln r₁ getragen, wie in Figur 13, und wird in die Verbindungsschiene der obern
zwei Kurbeln r ein Stift A eingesetzt, so beschreibt er bei der
Bewegung Kreise, deren Halbmesser ρ von der Größe r und
r₁ sowie von dem Winkel φ, unter welchem die untere
Kurbel zur obern gestellt ist, abhängt. Man findet leicht für
den Halbmesser den Werth φ =
√(r₂ + r₁²
– 2rr₁ cos φ) und für den Winkel δ, welchen derjenige Halbmesser
des erzeugten Kreises, der durch die Anfangsstellung des Stiftes
geht, mit der Richtung der untern Kurbel r₁ bildet,
Textabbildung Bd. 226, S. 240
Dreht sich, wie in Figur 14,
die Unterlagsfläche mit dem Zapfen der Kurbelschiene um, so
beschreibt der Stift der Zirkelschiene eine Epicycloïde,
wenn eine offene Schnur, und eine Hypocycloïde, wenn eine
gekreuzte Schnur zum Betriebe der zwei Scheiben verwendet wird.
Bewegt sich die Schlittenfläche mit gleichförmiger
Geschwindigkeit, während der Zirkel mit gleichförmiger
Winkelgeschwindigkeit sich dreht, so beschreibt sein Stift
gemeine Cycloïden. Wird die Schlittenfläche durch die
Kurbelwarze bewegt, während der Stift sich mit gleichförmiger
Geschwindigkeit in auf die Führungsrichtung senkrechter Richtung
bewegt, so beschreibt er eine Sinuslinie.
Wird, wie in Figur 16,
nicht nur die Fläche F, sondern auch
der Stift S durch eine in einem
Schlitze spielende Kurbelwarze bewegt und zwar so, daß sich die
Bewegungsrichtungen kreuzen, so beschreibt, wenn sich die zwei
Kurbeln mit gleicher Winkelgeschwindigkeit drehen, der Stift in
Folge der zwei oscillatorischen Bewegungen, wie leicht
nachzuweisen, eine Ellipse. Kreuzen sich die beiden
Bewegungsrichtungen unter rechtem Winkel, so sind die zur
Wirkung kommenden Längen der Kurbelschienen die Halbachsen
der entstehenden Ellipse; ist der Kreuzungswinkel hingegen ein
beliebiger, beispielsweise (φ), so entsprechen die Längen der beiden
Kurbelschienen den diesen Winkel φ einschließenden conjugirten Halbmessern der
entstehenden Ellipse.
Dieser Art der Zusammenstellung eines Ellipsographen, welche der
praktischen Ausführung – unter Voraussetzung, daß man
sich mit Verwendung eines Stiftes zum Verzeichnen der Ellipse
begnügt – keine namhaften Schwierigkeiten entgegensetzt,
könnte übrigens gegenüber den vorher besprochenen Ellipsographen
nur das als Vortheil angerechnet werden, daß bei letzterem die
Kurbelschienenlängen gleichzeitig auch die Längen der
betreffenden Halbachsen oder conjugirten Durchmesser sind, also
die Einstellung der Kurbelschienen auf gegebene Halbachsen oder
conjugirte Halbmesser eine directe ist.
Würde statt des Schlittens S (Fig.
10) der Stift die durch eine Kurbelschiene und Schlitz
hervorgerufene oscillalorische Bewegung erhalten und um die
Achse der Zirkelschiene statt eines Stiftes eine Fläche rotiren,
so beschreibt der durch die Kurbelschiene bewegte Stift Curven,
die ihrem Charakter nach zu den Herzlinien gehören, und welche
die gemeine Cardioïde und den Kreis als specielle Fälle
in sich schließen. Bewegt sich der Stift mit gleichförmiger
Geschwindigkeit und wirkt auf eine unter ihm mit gleichförmiger
Winkelgeschwindigkeit rotirende Fläche, so beschreibt er
archimedische Spiralen.
Tafeln