| Titel: | Theorie der Deprez-Umsteuerung; von Victor H. Sirk in Pola. |
| Fundstelle: | Band 221, Jahrgang 1876, S. 97 |
| Download: | XML |
Theorie der Deprez-Umsteuerung; von
Victor H. Sirk in
Pola.
Mit Abbildungen auf Taf.
III [a.c/1].
Sirk, Theorie der Deprez-Umsteuerung.
Der Umsteuerungsmechanismus von Deprez, von welchem
bereits in diesem Journale (* 1876 219 7) berichtet
wurde, besteht aus einem kreisförmigen, in Führungen M,
N (Fig.
1) verschiebbaren Gleitrahmen, welcher direct die Führung des gewöhnlichen
Muschelschiebers besorgt. Der Excenterarm EA.
überträgt die Bewegung des Excenters auf den Gleitrahmen, und es kann das Gleitstück
A mittels der Hängeschiene AB durch den Reversirhebel BCD gehoben oder gesenkt, bezieh, das Gelenk A in den beiden Enden des bogenförmigen Schlitzes KL eingestellt werden. Das Excenter ist der
Dampfkurbel diametral gegenüber aufgekeilt, der Schlitz des Gleitrahmens nach einem
Kreisbogen geformt, dessen mittlerer Halbmesser gleich der Excenterstangenlänge EA = 1 ist. Die Aufhängung des Excenterarmes muß
derart gewählt werden, daß das Gelenk A nahezu an eine
zur Führungsmittellinie MN parallele Bahn HJ (Fig. 2) gebunden
erscheint. Die Figur
2 stellt das Schema des Mechanismus dar, und es kann EOF unmittelbar als Drehungswinkel w der Kurbel aufgefaßt werden, weil den positiven wie
den negativen Winkeln ohnedies der gleiche Kolbenweg entspricht und auf diesen die
Dampfvertheilung bezogen werden soll. Es mag nun irgend ein Punkt des Gleitrahmens
als Schiebermittel angesehen werden, weil für horizontale Verschiebungen alle Punkte
dem gleichen Bewegungsgesetze folgen. Denkt man sich das Schleifstück in der
Entfernung AF = y von
der Führungsmittellinie eingestellt und bezeichnet OE = r die Excentricität, so ergibt sich
unmittelbar aus dem geometrischen Zusammenhang der Figur 2:
Textabbildung Bd. 221, S. 97
Die Entfernung des Schiebermittels von dem Wellencentrum für
die beiden todten Punkte bestimmt sich:
OF₁ = r + √(l² – y²) und OF₂ =
– r + √(l² – y²),
weshalb der Abstand des Schwingungsmittelpunktes X für ein gleiches lineares Voreilen OX = (OF₁ + OF₂)/2 = √(l² – y²) wird.
Die Gleichung des Schieberweges oder die jeweilige Entfernung des Schiebers vom
Mittelpunkte der Schwingung ist nun für den Drehwinkel w:
Textabbildung Bd. 221, S. 98
und, für die Wurzelgrößen die ersten zwei Glieder der Reihe
gesetzt, näherungsweise:
Textabbildung Bd. 221, S. 98
wovon endlich noch das letzte Glied vernachlässigt werden
kann, und sich somit die Gleichung ergibt:
s = r cos
w + yr/l sin w +
Z,
in welcher Z das Fehlerglied
bedeutet. Die Gleichung des Schieberweges wurde also in der von Zeuner aufgestellten allgemeinen Form s = A cos w + B sin w + Z dargestellt, und das
Zeuner'sche Kreisdiagramm kann unmittelbar zur Untersuchung der herbeigeführten
Dampfvertheilung verwendet werden, indem A = r und B = ry/l, für das gewählte y
gerechnet, die doppelten Mittelpunktscoordinaten ergeben. Die Gleichung des
Schieberweges trägt das eigenthümliche Gepräge der Umsteuerung in sich: für ein
negatives y, d.h. wenn das Schleifstück über den todten
Punkt des Schlitzes unter der Führungsmittellinie eingestellt wird, erscheint B entschieden negativ. Man gelangt jedoch wieder auf den
gleichen Schieberweg, d. i. zur richtigen Dampfvertheilung, indem man (– w) statt w setzt, d.h. wenn
die Drehung im entgegengesetzten Sinne erfolgt, weil sodann cos w als negativer Ausdruck wieder den ursprünglichen positiven Werth
herbeiführt.
Kreisdiagramm für die
Quadrantenstellungen der Kurbel.
Bezeichnen a und b (Fig. 3) die
Coordinaten des Mittelpunktes der Schieberkreise, so muß offenbar
a = OA/2
= F(0)/2, b = OB/2 = F (90)/2
sein, und es können diese leicht durch Substitution der Werthe
0 und 180, 90 und 270 in
die Function des Schieberweges gefunden werden, wobei sich ergibt, daß
Textabbildung Bd. 221, S. 99
Man verzeichnet diese Kreisgruppen, indem man aus O (Fig. 4) mit der
Excentricität OA = r und OC = 1 der Excenterstangenlänge zwei Kreise verzeichnet,
in D, D, und D₂
beliebige Stellungen des Schleifstückes zur Untersuchung wählt, so daß DH = y ist, durch
diese Punkte Parallele zur X-Achse zieht, und aus
K und L mit der
Excenterstangenlänge OD = KE
= LF Kreisbögen verzeichnet, welche die den variablen
y entsprechenden Ordinaten an den Parallelen
abschneiden. Errichtet man in A und B Perpendikel, trägt AP =
DE und BQ = DF auf, so erhält man in P
und Q die Mittelpunkte der Schieberkreise, welche auf
die bekannte Weise ein Bild der Schieberbewegung geben. Analog erhält man für jede
der gewählten Stellungen die Mittelpunkte der Schieberkreise, welche in Figur 4
dargestellt erscheinen. Der Beweis für die Richtigkeit der Construction erhellt aus
dem geometrischen Zusammenhange der Figur 4:
Textabbildung Bd. 221, S. 99
(Nach dem angegebenen Verfahren erhält man den Schieberkreis
in doppelter Größe.)
Die erlangten Schieberkreise erschöpfen den Schieberweg bei den Quadrantenstellungen
der Kurbel vollkommen und wären für den Entwurf solcher Steuerungen anzuempfehlen,
nachdem bei diesen Stellungen nahezu die Momente der Canaleröffnung und Schließung
erfolgen.
Diese Kreisgruppe bringt das durch die Deprez-Steuerung factisch erreichte,
für alle Expansionsgrade gleichbleibende, constante Voreilen anschaulich zur vollen
Geltung.
Aus der Gleichung des Schieberweges kann entnommen werden, daß die Centralcurve
dieser Kreisgruppe wie bei Gooch's und Fink's Coulisse eine Parallele zur Y-Achse ist, weil A =
r von y unabhängig
ist.
Kreisdiagramm für den vollen
Ausschub.
Eine zweite Gruppe, welche im Verein mit der eben aufgestellten Kreisgruppe die durch
diese Steuerung hervorgerufene Schieberbewegung Heller beleuchtet, erhält man durch
folgende Betrachtung: Die Function des Schieberweges kann im Allgemeinen durch ein
Kreisdiagramm dargestellt werden, und man findet dessen Durchmesser OE als das
Maximum von s = F (w). Der erste Differentialquotient muß ds/dw = 0 sein, woraus der
Winkel FOA = α (Fig. 5)
bestimmt werden kann. Der Werth des Maximums selbst stellt den Durchmesser OK des Schieberkreises dar.
Textabbildung Bd. 221, S. 100
Dieser Werth gleich Null gesetzt, geht w in α über, weshalb
Textabbildung Bd. 221, S. 100
Für sin α aufgelöst, findet
man sin α = ± y/(l ± r).
Der Werth (+ y/[l + r])
entspricht dem Winkel α, (– y/[l – r]) einem
Winkel 180 + α', welcher den zweiten
Schieberkreis trägt. Der zweite Differentialquotient ist für den ersten Werth
negativ und F (w) ein
Maximum, für den Werth (– y/[l – r]) entschieden positiv, weshalb F (180 + α') dem
Minimum (negatives Maximum) entspricht. Die Durchmesser der Schieberkreise findet
man als den Werth des Maximums, indem man α in
F (w) einsetzt, mit
Textabbildung Bd. 221, S. 100
Verzeichnet man sich nun mit der Excenterstangenlänge OC = 1 (Fig. 5) einen Kreisbogen,
zieht durch die im vorigen Falle gewählten Punkte D,
D₁ Parallele zur X-Achse, trägt BC = CA = r auf und beschreibt aus O durch A und B Kreisbögen, so schneiden diese unmittelbar auf den
gezogenen Parallelen die Durchmesser der Schieberkreise ab. Verbindet man E und F mit O, so sind zugleich die Winkel FOA = α und EOA = α' dargestellt. Trägt man DF = OP, DE = OQ
auf, so erhält man die Mittelpunkte des ersten Kreispaares für die Stellung des
Schleifstückes in D und DH =
y.
Die Kreisgruppen stellen die Schieberbewegung in der Nähe des vollen Ausschubes
erschöpfend dar, obwohl sie das constante Voreilen nicht veranschaulichen und daher
für die Praxis nur von untergeordnetem Werthe sind. Die Centralcurven dieser Gruppe
von Schieberkreisen sind Parabeln höherer Ordnung, deren beide Aeste nach rechts
offen liegen. Der Beweis für die Richtigkeit der Construction kann leicht dem
folgenden entnommen werden.
Textabbildung Bd. 221, S. 101
Die Schieberbewegung wurde daher durch drei wesentlich
verschiedene Kreisgruppen ersetzt, welche die Dampfvertheilung auf die bekannte
Weise kennzeichnen.
Die Kreisgruppen für die Quadrantenstellungen der Kurbel und für den Maximalwerth der
Function oder für den vollen Ausschub lassen kein Fehlerglied erkennen, was als ein
Mangel der eingeschlagenen Methoden angeführt werden muß, obwohl anderseits leicht
construirbare durchsichtige Coordinaten der Schieberkreise erhalten wurden.
Einfluß des Fehlergliedes.
Wird die aus der Reihenentwicklung erhaltene Gleichung des Schieberweges s = r cos w + ry/l sin w als die durch das Kreisdiagramm dargestellte
Normaldampfvertheilung angenommen, so stellen die nachfolgenden Glieder aus der
Reihenentwicklung, welche in dem Ausdrucke Z
zusammengefaßt wurden, die Abweichung von dem im Kreisdiagramm gegebenen Schieberweg
dar. Das Fehlerglied erscheint in der Form Z = C sin³w,Textabbildung Bd. 221, S. 101 und es findet die größte Abweichung statt, wenn Z ein Maximum wird. (dZ/dw) = 3 l sin²w cos w, welches für w = 0
und 180, 90 und 270 Null wird. Bei den todten Punkten ist die Abweichung gleich
Null, und der Kreis der ersten Gruppe erschöpft den Schieberweg. Bei den Drehwinkeln
90 und 270° findet ein Maximum der Abweichung statt, wie der zweite
Differentialquotient lehrt. Nachdem das Abschneiden des Dampfes häufig bei halben
Füllungen stattfindet, so wäre die erste Kreisgruppe in der Praxis für den Entwurf
von derlei Steuerungen nicht anzuempfehlen, nachdem sie den Unregelmäßigkeiten der
Schieberbewegung in keiner Weise gerecht wird, wie die Gruppe der andern
entwickelten Schieberkreise. Das Bewegungsgesetz des Schiebers zeigt eine so große
Aehnlichkeit mit
Fink's Steuerung, daß nur eine genaue Untersuchung zum Ausspruche berechtigt, daß
bei der Deprez-Steuerung die beirrende Abweichung von der idealen
Dampfvertheilung größer als bei Fink's Steuerung ist, weshalb bei sonst gleicher
Anwendbarkeit dem letztern Umsteuerungsmechanismus der Vorzug gegeben werden
muß.
Betrachtung des
Schieberdiagrammes.
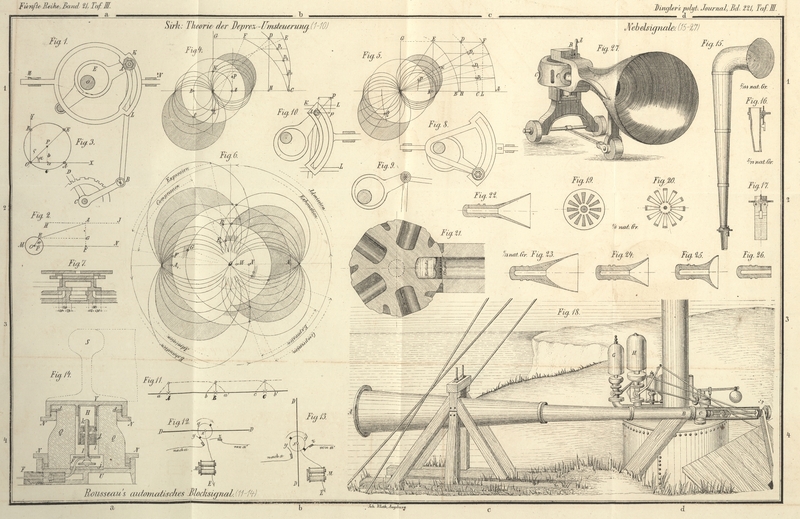
Figur 6 stellt
die aus sorgfältigen Uebertragungen der Schieberwege für den Vor- und
Rückwärtsgang bei einer Versuchssteuerung entstandenen Kreisdiagramme dar. Die aus
einer Reihe von Versuchen als die zweckentsprechendst befundene Modellsteuerung
hatte als Hub des Excenters r = 25mm, Länge der Excenterstange 175mm, Maximalwerth des Abstandes y = 125mm,
wobei ein Schieberweg von 100mm stattfand;
die Länge der Aufhängestange war 500mm, die
äußere Deckung mußte mit 30mm gewählt
werden, um ein lineares Voreilen von 5mm zu
erhalten. Die Aufhängung des Excenterarmes muß derart gewählt werden, daß die Sehne
des bei der Bewegung beschriebenen Kreisbogens zur Führungslinie parallel ist. Die
Hängeschiene soll so groß, als mit der Sicherheit der Construction verträglich ist,
mindestens jedoch 12r gewählt werden. Die Länge des
Hebels BC ist gleich der Länge des Excenterarmes, und
C befindet sich senkrecht unter dem Wellencentrum.
Die größte Dimension y darf l–2r nicht überschreiten.
Bei Betrachtung der Schiebercurven Figur 6 drängt sich zuerst
die Beobachtung auf, daß der Schieber bei der erforderlichen Adjustirung auf
gleiches Voreilen für gegenüberliegende Stellungen der Dampfkurbel ungleiche
Ausschube zu beiden Seiten des Schwingungsmittelpunktes erfährt, – eine
Eigenthümlichkeit, welche, wie die Construction erkennen läßt, durch die beschränkte
Länge der Excenterstange hervorgerufen wird und in dem Maße allen Steuerungen
anhaftet, als die Bewegungsübertragung durch kurze Excenterstangen besorgt wird. Die
einzelnen Phasen der Dampfvertheilung werden daher für die beiden Kolbenbewegungen
ungleichmäßig herbeigeführt, und die Dampfvertheilung ist nicht vollkommen
theoretisch richtig. Bei gleicher äußerer Deckung OA =
a erhielte der Cylinder bei der Bewegung des Kolbens
von rechts nach links AM (45 Proc.) und beim Rücklauf
A₁N (66 Proc.)
Füllung. Diese Verschiedenheit der Admissionsperiode herrscht durch alle
Expansionsgrade und wächst mit der größern Füllung. Dem Uebelstande kann durch
ungleiche Ueberdeckungen theilweise begegnet werden. Wählt man am rechten
Dampfcanal, wo die geringere Füllung stattfindet, eine kleinere äußere und am
entgegengesetzten Schieberlappen eine kleinere innere Deckung, so erreicht man zum mindesten für die am
meisten in Aussicht genommenen Expansionsgrade gleiche Füllungen und gleiche
Compression.
Das Schieberprofil, Figur 7, bei einer Canalweite von 30mm zeigt 20 und 24mm links, 12
und 30mm rechts Deckung und läßt für die
Expansionsstufen D bis D₂ einen ruhigen Gang der Maschine erwarten. Für D₁ erfolgt bei 50 Proc. Füllung gleichmäßige Dampfvertheilung. Zum
Ansetzen der Maschine kann 60 Proc. Füllung angewendet und die Maschinenkraft ohne
Nachtheil auf 35 Proc. vermindert werden. Die Dampfvertheilung, welche bei dem
vorgeführten Schieberprofil die Modellsteuerung herbeiführt, ist aus nachfolgendem
Schema ersichtlich.
Links
Rechts
für D
für D₂
für D
für D₂
Füllung
60 Proc.
38 Proc.
66 Proc.
33 Proc.
Expansion
37 „
55 „
28 „
53 „
Vorausströmung
3 „
7 „
6 „
14 „
Ausströmung
71 „
43 „
70 „
60 „
Compression
26 „
43 „
29 „
38 „
Voreinströmung
3 „
14 „
1 „
2 „
Schlußbemerkung.
Der Gleitrahmen hat bei der in Figur 1 dargestellten Form
bedeutende Dimensionen, welche die Stabilität und den ruhigen Gang der äußern
Steuerung gefährden, oder massive Detailconstruction und lange Führungen
voraussetzen. Nachdem die excentrische Scheibe und der Gleitrahmen nicht in der
gleichen Ebene arbeiten, kann der Rahmen bedeutend verkleinert werden, so daß er die
in Figur 8
dargestellte Form zeigt und neben der excentrischen Scheibe schwingt. Der
Steuerungsapparat wird dadurch compacter und leichter, wie auch die Führung
sicherer. Gestatten Raumverhältnisse eine Schubstange von mindestens 41 Länge
einzuschalten, welche das Schleifstück mit der Schieberstange in Gelenken verbindet,
so kann, ohne große Abweichung in der Dampfvertheilung für zwischen engen Grenzen
veränderliche Füllung, der Gleitrahmen ganz weggelassen werden, wie die Figur 9 zeigt.
Eine solche Construction wäre nur für kleine Maschinen oder Locomobilen anzuwenden,
bei welchen Dampfökonomie hinter Einfachheit zurücksteht. Für solche wäre die
Umsteuerung mit variabler Füllung eine durch geringe Schwierigkeiten erkaufte
nützliche Zugabe. Der Schieber schwingt nur für ein Expansionsverhältniß in seinem
Mittel, und der Dampf muß während des Stillstandes durch das Drosselventil
abgesperrt werden.
Bei sicherer Führung der Enden K und L der Coulisse auf der Seite des Schieberkastens könnte
man davon Abgang nehmen, den Rahmen zu schließen und auf der entgegengesetzten Seite
der Achse noch eine Führung zu geben, wie dies in Figur 10 dargestellt
ist.
Der Nachtheil des ungleichen Ausschubes, welcher dieser Steuerung eigenthümlich ist,
wurde im Vorhergehenden besprochen und demselben durch ein unsymmetrisches
Schieberprofil größtentheils begegnet, wobei ein anderer Uebelstand hervorgerufen
wurde, welcher den gleichmäßigen Gang zu stören droht. Eine Betrachtung der Figur 6 zeigt,
daß das lineare Voreilen am rechten Dampfcanal in Folge der geringern äußern
Ueberdeckung constant größer bleibt als am linken Dampfcanal. Die Adjustirung des
Schiebers erfordert größere Genauigkeit und Sachkenntniß. Aus Figur 6 ist ferner
ersichtlich, daß der Ausschub bei den todten Punkten für alle Füllungen unverändert
gleich der Excentricität ist, weshalb die äußere Ueberdeckung groß – nur um
den geringen Betrag des linearen Voreilens geringer gewählt werden muß als der Hub
des Excenters. Eine große äußere Ueberdeckung bringt große Schieberdimensionen mit
sich, welche einen erheblichen Dampfdruck empfangen und bedeutenden
Reibungswiderstand verursachen, welcher Entlastungsvorrichtungen bedingt. Der
Ausschub ist im Verhältniß zur Canalbreite im Vergleich mit andern
Coulissensteuerungen größer, und die Bewegung des Schiebers bedingt einen vermehrten
Kraftaufwand, welcher den Nutzeffect der Maschine verkürzt. Eine größere äußere
Ueberdeckung verursacht ferner einen schleichenden Abschluß der Dampfwege, in Folge
dessen der Dampf besonders bei geringen Füllungsgraden am Schlusse der
Admissionsperiode gedrosselt wird.
Um durch die der Steuerung anhaftende bedeutende Compression des Hinterdampfes keine
Spannungen hervorzurufen, welche die Schieberplatte abheben würden, und anderseits
die Compressionsarbeit durch den zurückgehaltenen Dampf zu decken, müssen die
Zuleitungscanäle und der sogen, schädliche Raum groß gehalten werden. Dadurch wird
aber das Medium vergrößert, welches eine nutzlose Wärmeabgabe des zuströmenden an
den abgehenden Dampf vermittelt. Große schädliche Räume begünstigen die Condensation
des Arbeitsdampfes bei seinem Zutritt in den Cylinder an den vom abströmenden Dampf
abgekühlten Wänden der Dampfcanäle.
Denkt man sich den Steuerungsmechanismus in der in Figur 10 verzeichneten
Lage, so übt das Excenter seinen Schub in der Richtung nach P aus, welche mit dem Sinne der Bewegung des Gleitrahmens einen stumpfen
Winkel bildet. Die Componente p, welche die
Bewegungshindernisse des Schiebers überwindet, fällt für diese Stellung gering aus,
während ein bedeutender Zug auf die Hängeschiene ausgeübt und auf den Zapfen A übertragen wird. Die Kraftübertragung stellt sich um
so ungünstiger dar, je größere Füllung gegeben wird. Der Steuerungsmechanismus ist
daher einer großen Abnützung ausgesetzt und wird einen unruhigen Gang verursachen,
weshalb y = l – 2r als Maximalwerth festgesetzt wurde.Derselbe Einwand wurde auch in der frühern Abhandlung (1876 219 8) gegen diese Steuerung erhoben.Die Red.
Die Mängel der Deprez'schen Steuerung wurden im Vorhergehenden besprochen, ohne deren
Vorzüge hervorzuheben, weil der Charakter der Einfachheit, welcher mit einem Minimum
an beweglichen Theilen eine für manche Zwecke nur durch complicirtere Mechanismen
erreichbare variable Füllung mit Umsteuerung vermittelt, zu augenscheinlich ist, um
besonders betont zu werden. Nichts destoweniger könnte die vorliegende Steuerung nur
in wenigen Fällen die Stephenson'sche Coulisse mit Vortheil ersetzen. Die ungünstige
Kraftübertragung ermöglicht nur bei mäßigen Tourenzahlen einen ruhigen Gang, so daß
die Deprez-Steuerung bei hoher Kolbengeschwindigkeit ausgeschlossen scheint,
obwohl sie sich der Dampfvertheilung nach für höher gespannte Dämpfe mit directer
Abströmung empfehlen würde. Die Bedienung der Umsteuerung ist sicher und rasch,
erfordert jedoch im Vergleich mit andern Vorrichtungen einen größern Kraftaufwand,
weil der Dampfschieber durch einen größern Weg geführt werden muß. (Auszugsweise
nach Stummer's Ingenieur, 1875 Nr. 95 bis 97.)
Tafeln