| Titel: | Dynamometer von Heinrich King, Ingenieur in Glasgow. |
| Fundstelle: | Band 192, Jahrgang 1869, Nr. XVII., S. 82 |
| Download: | XML |
XVII.
Dynamometer von Heinrich King, Ingenieur in Glasgow.
Nach Engineering, Februar 1869, S.
121.
Mit Abbildungen auf Tab.
III.
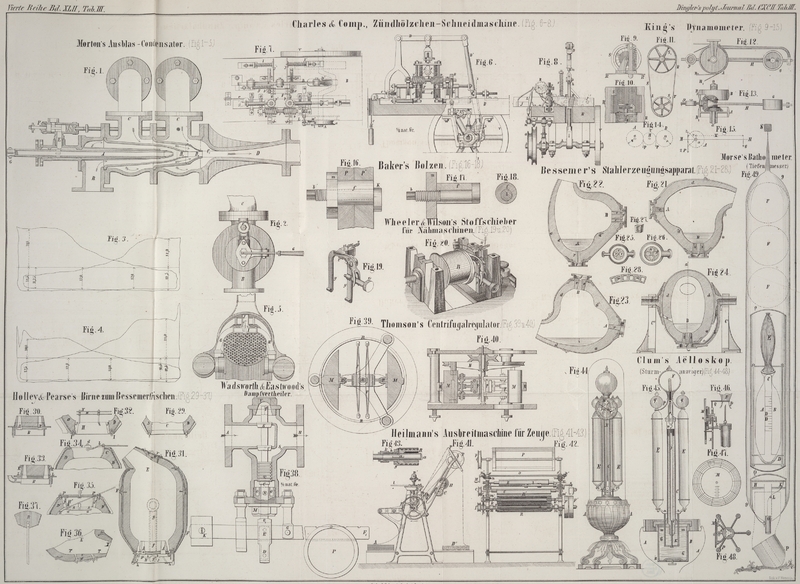
King's Dynamometer.
In Fig. 9
– 13
sind zwei Dynamometer dargestellt, wie sie vom Ingenieur King in Glasgow construirt werden.
Die Wirkung des in Fig. 9 – 11 gezeichneten
Dynamometers gründet auf
dem Satze, daß die von einem Riemen R übertragene Kraft
P gleich ist dem Unterschiede der Spannungen (T und t) des führenden und
des geführten Riementheiles, somit die Arbeit aus dem Product dieser Kraft P = T—t in die auf gewöhnlichem Wege zu bestimmende
Geschwindigkeit v gefunden wird.
Die beiden Riemenenden R, R
sind nun durch eine hufeisenförmig gebogene, entsprechend kräftige Stahlfeder S verbunden, wie dieß aus Fig. 9 und 10 zu entnehmen ist,
ähnlich wie aus Fig. 11, so daß dieser Federapparat an der Bewegung des Riemens Theil
nimmt. Je nachdem die Spannung im Riemen die größere T
oder die kleinere t ist, wird diese Feder an dem offenen
Theil auseinander- oder zusammengezogen. Die in Folge der Kraftübertragung
P um T—t erhöhte Spannung t wird
durch eine Sperrradanlage auf eine Theilscheibe ersichtlich gemacht, indem das
Sperrrad bei dem Auseinanderziehen der Federenden um einige Zähne weiter gerückt
wird, während der Sperrkegel beim Zusammengehen der Enden der Feder lose
zurückgleitet.
Unter der Voraussetzung, daß die Theilung an der Theilscheibe in richtigem
Verhältnisse mit der Kraftäußerung steht, ist die Berechnung der Größe der letzteren
allerdings sehr einfach. Findet man z. V. die mittlere Differenz der Spannungen T und t mit 100 Pfunden und
ist die Geschwindigkeit 330 Fuß per Minute, so ist die
übertragene Arbeit 100 × 330 = 33,000 Fußpfund oder eine Watt'sche Pferdekraft.
Das zweite Dynamometer ist aus Fig. 12 und 13 zu
entnehmen. Die Maschine oder eine motorische Kraft wird durch einen Riemen R1 mit der Scheibe A verbunden, während die Scheibe B durch den Riemen R2 mit der zu prüfenden Maschine in Verbindung gesetzt wird. Die Scheiben
A und B haben gleichen Durchmesser und laufen lose auf der gemeinschaftlichen Achse a. An
jeder Scheibe ist ein Kegelrad fix, welche gleich großen
Räder in ein drittes eingreifen, das an dem kürzeren Ende eines zweiarmigen Hebels
H gelagert ist, dessen Drehungspunkt in der Achse
der Scheiben A,B liegt. Das
längere Ende des Hebels ist mit einer Theilung versehen, welche den Abstand des
verstellbaren Gewichtes G (100 Pfund) vom Drehungspunkt
oder auch sofort die jeweilig übertragene Arbeit angibt. Für die Gleichgewichtslage
des Hebels H, welche durch die entsprechende Einstellung
des Gewichtes G erzielt wird, findet man die von der
Scheibe A auf die Scheibe B
resp. die zu prüfende Maschine während einer Umdrehung übertragene Arbeit in
Fußpfunden, wenn man das halbe Product aus dem in Pfunden ausgedrückten Gewichte G mit dem in Fußen berechneten Umfang eines Kreises von dem Radius gleich
dem Abstand des Gewichtes vom Drehpunkte des Hebels bildet.Die Begründung der Wirkungsweise dieses — übrigens nicht ganz neuen — Dynamometers ist einfach
folgende:Das Rad A (Fig. 14)
übertrage auf jenes B die Kraft P; der Druck auf die Achse H des Zwischenrades ist dann 2 P und dieser wirkt im Abstand r am kürzeren Hebelarm, während das Gewicht G im Abstande X das
Gleichgewicht hält (Fig. 15), somit
die Gleichung gilt2P r =G X 1Während einer Umdrehung überträgt aber die Scheibe
resp. das Rad A die ArbeitL = P · 2π r 2Aus 1 folgt π G X = P · 2π rSomit ist die während einer Umdrehung übertragene Arbeit L = π G X =
2π × · G/2 = dem halben
Product aus dem Gewichte G (Pfd.) in den Umfang
des mit dem Abstand X als Radius gezogenen
Kreises (in Fußen ausgedrückt).J. Z.
Das Gewichtchen g dient nur zur Ausgleichung des
Uebergewichtes des längeren Hebelarmes.
J. Z.
Tafeln