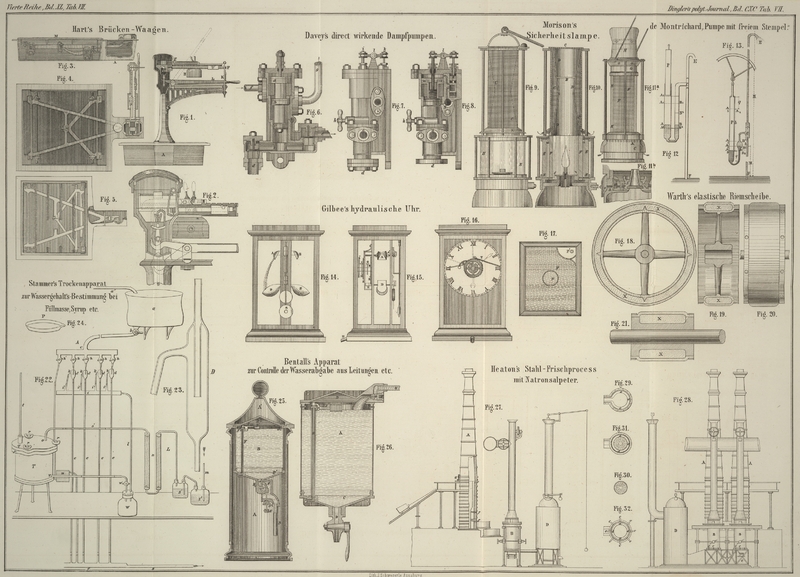
| Titel: | Ueber eine Pumpe mit freiem Stempel; von Marquis de Montrichard. |
| Fundstelle: | Band 190, Jahrgang 1868, Nr. CX., S. 433 |
| Download: | XML |
CX.
Ueber eine Pumpe mit freiem Stempel; von
Marquis de
Montrichard.
Im Auszug aus Les Mondes, t. XVIII p. 152 et 165; October
1868.
Mit Abbildungen auf Tab.
VII.
de Montrichard, Pumpe mit freiem Kolben.
„Der neuen Maschine haben wir den Namen Pumpe mit freiem Kolben gegeben, weil
dieselbe mittelst eines Kolbens functionirt, welcher eine Gestalt annehmen kann, die
von jener der inneren Wände des Pumpenstiefels ganz verschieden ist, so daß, was bei
keinem anderen Systeme ausführbar ist, bezüglich der Dimension und der Adjustirung
keine Abhängigkeit in dieser Beziehung besteht. Diese Pumpe kann zur Verdichtung und
Verdünnung der Gase, zum Emporheben des Wassers und überhaupt in allen Fällen
benutzt werden, wo die Pumpen der verschiedenen Systeme in Anwendung kommen. Die
Bewegung des Stempels dieser Pumpe wird auf die Flüssigkeiten, welche deren
Einwirkung ausgesetzt werden sollen, mittelst einer Flüssigkeit fortgepflanzt, von
welcher der fortgepflanzte Druck in directem Verhältnisse mit ihrer Dichte steht.
Als Typus der Pumpe mit freiem Stempel haben wir daher die Quecksilberpumpe
angenommen, deren Beschreibung wir geben werden. Die Quecksilberpumpe bietet eine
besondere Eigenheit dar, welche von vornherein paradox erscheint. Der Kolben dieser
Pumpe hat keine Reibung an den Wänden des Pumpenstiefels zu überwinden; die Luft und
das Quecksilber circuliren frei im Pumpenstiefel und um den Kolben. Trotzdem kann
man gegen die Flüssigkeiten und die Gase unbegrenzte Pressungen ausüben, ohne daß
eine Entweichung derselben durch den Körper der Pumpe möglich ist. Man kann also
voraussetzen, daß selbst bei hohen Drucken die Quecksilberpumpe am leichtesten zu
construiren ist und bei ihrem Gebrauche am wenigsten in Unordnung kommt. Wir hoffen,
daß durch die Beschreibung und nähere Erörterung dieser Maschine diese Behauptungen
gerechtfertigt werden können.
In einer doppelt gekrümmten Röhre (Fig. 12) sey Quecksilber
bis zu einer gewissen Höhe A, B enthalten. Der eine
Schenkel B dieser Röhre steht mit dem Rohre F,
E in Communication, welches mit zwei Ventilen versehen ist; letztere
gestatten den Flüssigkeiten in der Richtung FC, CE zu
circuliren, ohne daß dieselben wieder rückwärts in entgegengesetztem Sinne strömen
können. Im anderen Schenkel A der Quecksilberröhre ist
ein massiver Kolben P beweglich angebracht; die Gestalt
dieses Kolbens kann eine ganz andere seyn, wie jene des Stiefels A. Der atmosphärische Druck wirkt frei auf den Kolben
und auf das Quecksilberniveau in A. Wird der Kolben in
das Quecksilber eingetaucht, so verdrängt er ein gewisses Volumen desselben. In
Folge dieser Einwirkung erhebt sich das Quecksilberniveau in den beiden Schenkeln
A, B, und es wird daher ein Theil der zwischen den
beiden Klappen und der Oberfläche des Quecksilbers in B
enthaltenen Luft durch die Oeffnung E entweichen müssen,
wenn der Stempel P in das Quecksilber eingetaucht wird.
Zieht man den Stempel wieder aus dem Quecksilber zurück, so fallen die
Quecksilberniveaux, und es wird daher eine Verdünnung der Luft zwischen F und B eintreten müssen.
Dieser Aspiration folgt ein neues Ausströmen, und es wird daher wieder eine
Quantität Luft durch die Oeffnung E austreten können.
Indem wir also in dem Schenkel B durch abwechselndes
Eintauchen und Herausziehen des Kolbens der Röhre A das
Quecksilberniveau fortwährend ändern, bringen wir die Pumpe zur Thätigkeit.
Benutzt man diese Pumpe zum Wasserheben und untersucht sie in dem Momente, wo sie in
voller Thätigkeit sich befindet, so sieht man, daß wenn die Quecksilberniveaux an
der oberen und unteren Seite ihre äußersten Grenzen erreicht haben, dieselben
niemals in gleicher Höhe in den beiden Schenkeln seyn werden, und daß in dieser
Beziehung die größten Variationen in der Röhre A
hervortreten. Wenn z. B. während des Niederdrückens das Quecksilberniveau im freien
Schenkel bis zu A2
kommt, so erreicht es im anderen Schenkel nur die Höhe bis B1; die Quecksilbersäule A1, A2 hält der Wassersäule B1, E das
Gleichgewicht. Wird hierauf der Kolben wieder aus dem Quecksilber herausgezogen, so
fällt in seinem Stiefel das Niveau bis A3, während es im anderen Schenkel bloß
bis B2 fällt; die
Quecksilbersäule B2, B3 hält der Wassersäule F, B2 das
Gleichgewicht. Das zwischen den Niveaux B1, B2
enthaltene Volumen ist gleich der während des Saugens in den Apparat eingeführten
Wassermenge, und diese wird bei dem darauffolgenden Niederdrücken zum Austreten
gebracht. Man ersieht, daß wenn die Pumpen von geringerer Ausdehnung eine Form
annehmen können, wie sie beiläufig schematisch in Fig. 12 gezeigt ist, bei
Pumpen von großen Dimensionen mancherlei Aenderungen ihrer Theile eintreten müssen,
und daß dann die Gestalt der letzteren je nach den gegebenen Umständen berechnet
werden muß, um den
Anforderungen zu genügen. Eine solche Rechnung wollen wir hier versuchen. Die
Elemente, welche gewöhnlich angegeben werden, sind: die Höhe H, bis zu welcher das Wasser gehoben werden soll; die Höhe M, des centralen Theiles der Maschine oberhalb des
Wasserreservoirs oder der Quelle; das Volumen V des
Wassers, welches während der Zeit T geliefert werden
soll und das specifische Gewicht D des Quecksilbers;
hierzu kann man noch die Anzahl der Kolbenspiele N,
welche die Maschine in der Zeiteinheit ausführt, nehmen, eine Zahl, welche eine
gewisse Grenze nicht überschreiten darf, damit das Quecksilber nicht aus dem Stiefel
A hinausgeschleudert wird. Nennt man k den verticalen Lauf des Quecksilbers in dem Arme B, und b den mittleren
horizontalen Querschnitt des durchlaufenden Raumes, so wird die bei den
Kolbenspielen gehobene Wassermenge gleich b k N,
also
b k N = V/T und b k = V/TN
(1
Hierbei ist vorausgesetzt, daß die Maschine in voller Thätigkeit sich befindet. Wenn
beim Aufwärtsgehen des Kolbens das Quecksilber im zweiten Schenkel bis B2 fallen soll, so muß
die Quecksilbersäule von der Höhe B3, B2
oder m der durch Saugen gestiegenen Wassersäule M das Gleichgewicht halten, so daß man also hat
m D = M,
sohin m = M/D (2
Nennt man h den vom Quecksilber durchlaufenen Raum A2, A3, so ersieht man, daß, wenn beim
Eintauchen des Kolbens in das Quecksilber das Niveau im zweiten Schenkel bis zu B1 steigen soll, die
Bedingung erfüllt werden muß:
(h - m - k) D = H - M - k, woraus sich ergibt:
Textabbildung Bd. 190, S. 435
Suchen wir jetzt die Relationen zwischen dem horizontalen Querschnitte a des Cylinders A, dem
Querschnitte a′ des Kolbens und dem Minimum q des nöthigen Kolbenlaufes beim Eintauchen. Beim
Einsenken des Kolbens verdrängt derselbe das Quecksilbervolumen a′, q, das sich
innerhalb der Querschnitte a - a′ auf eine Höhe h verbreitet, sowie in
einen Cylinder, dessen Capacität V/T seyn soll. Man hat
sohin:
Textabbildung Bd. 190, S. 435
Der größte Quecksilberdruck beim Eintauchen des Kolbens ist (5 s = a′ (q +
h) D, und die nöthige Anstrengung, um diesen
Druck zu überwinden, wenn p das Gewicht des Kolbens ist,
beträgt s - p = a′(q + h) D -
p.
Bei s - p = p, hat man
daher
p = ½a′(q + h)D
(6
Das Quecksilbervolumen v, welches zum Functioniren der
Pumpe nöthig wird, ist:
(7 v = (a - a′)(h + q) + bk + w, wenn w das in der
communicirenden Röhre bis zum Niveau B2 enthaltene Quecksilbervolumen
bezeichnet.“
Eine nach den vom Verfasser angegebenen Principien construirte Pumpe ist im Maaßstabe
von 1/50 in Fig.
13 dargestellt. Den einzelnen Theilen der Pumpe und deren Organen gibt er
besondere Namen; so heißt der Schenkel A der
Pumpenstiefel, der Schenkel B der Betriebsarm, die
Niveaudifferenz A2B1 (fig. 12) die Druckhöhe,
die Niveaudifferenz A3B2 die Saughöhe u. s. w.
Um über die Wirksamkeit einer derartigen Pumpe einigen Aufschluß zu geben, macht der
Verfasser bloß von einigen der oben angegebenen Formeln (nämlich Gleichung 2 und 3)
hier Anwendung, ohne auf die eigentliche Leistungsfähigkeit der Pumpe unter
Berücksichtigung der sich dabei darbietenden Bewegungshindernisse näher einzugehen.
— Soll die bei jedem Kolbenstoße gelieferte Wassermenge 5 Liter betragen, so
kann dieß durch verschiedene Anordnungen erreicht werden. Bei der vorliegenden soll
die sogen. Saughöhe m einer Quecksilbersäule von 50
Centimeter entsprechen, die also einer Wassersäule von 6,8 Meter das Gleichgewicht
hält. Die Höhe H der Wassersäule, welche bei einem
Quecksilberhub h von 4,68 Meter gehoben wird, beträgt
61,8 Meter. Da man leicht in 10 Secunden ein Kolbenspiel vollführen kann, so wird es
unter diesen Umständen möglich seyn, 30 Liter in der Minute oder 1800 Liter Wasser
in der Stunde zu liefern. Verdoppelt man alle Dimensionen (mit Ausnahme der
Aspirationshöhe), so erhält man 40 Liter Wasser bei jedem Kolbenhub auf eine Höhe
von 123,6 Meter, und wenn nur ein Kolbenspiel in 20 Secunden stattfindet, so beträgt
schon die in einer Stunde gelieferte Wassermenge 7200 Liter. „Man begreift
sohin, daß eine in den obersten Räumen eines Gebäudes angebrachte Dampfmaschine,
wenn diese eine Quecksilberpumpe in Bewegung versetzt, Effecte hervorzubringen
vermag, welche bis jetzt unmöglich waren. Ebenso kann eine Quecksilberpumpe,
welche das Wasser am Niveau der Flüsse heraushebt, bei eintretenden
Feuersgefahren Wasserstrahlen auf die höchsten Gebäude in den Städten führen;
sie kann sogar in der Atmosphäre Wasserstrahlen heben, welche bis zu den
Wolken sich zerstreuen, und dann in Nebelform, die Luft abkühlend, auf die Erde
zurückfallen, um dann durch die Wärme des Bodens in Dampf verwandelt zu werden.
Die Quecksilberluftpumpe kann das Wasser von einer Quelle nach einer anderen
oder bis zu den Städten überführen, aus dem Inneren der Erde u. s.
w.“ Auch im Kleinen lasse die Quecksilberpumpe mannichfache
Anwendungen zu, namentlich für chemische Laboratorien, für Destillationszwecke, zum
Gebrauche für die Injection der Bauhölzer, wobei dann die Anordnung nach dem
jeweiligen Zwecke gemacht werden kann.
Tafeln