| Titel: | Barbary's Gasdruckregulator. |
| Fundstelle: | Band 187, Jahrgang 1868, Nr. IX., S. 40 |
| Download: | XML |
IX.
Barbary's Gasdruckregulator.
Mit einer Abbildung auf Tab. I.
Barbary's Gasdruckregulator.
Der in Armengaud's
Génie industriel, September 1867, S. 141
veröffentlichte Gasdruckregulator von Barbary in
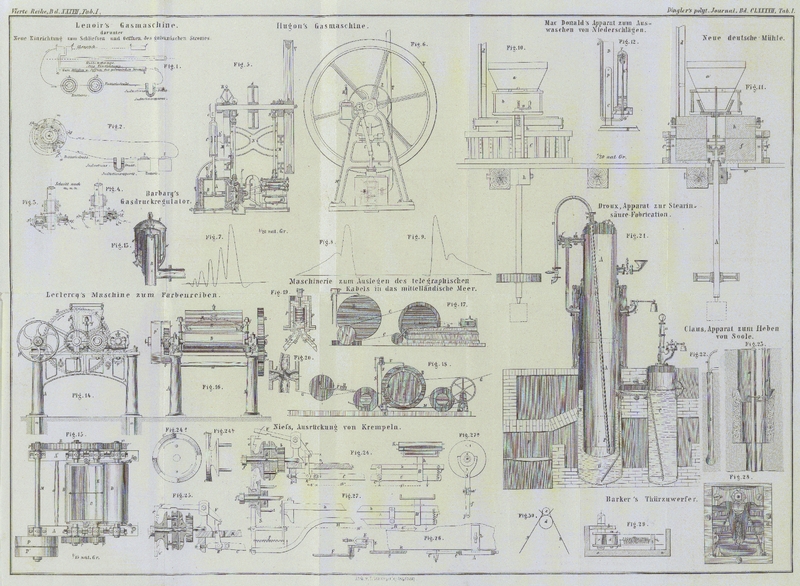
Chateauroux besteht, wie Fig. 13 zeigt, aus einem
cylindrischen, durch einen Deckel A' geschlossenen
Behälter A mit zwei concentrischen Röhren B und C; durch die Röhre B gelangt das Gas in den Apparat und in der Röhre C strömt es unter dem bestimmten Drucke ab. Die Glocke
D, welche beide Röhren bedeckt, trägt mittelst der
Stange t das Regulirventil v; besonders wesentlich ist die Form dieses Ventiles, welches den gewöhnlich angewendeten
spitzen Regulirkegel ersetzt. Letzterer hat nach Barbary's Ansicht den Nachtheil, daß er einen großen Hub der Glocke
bedingt, eine zu große Empfindlichkeit besitzt, so daß er jeder kleinen Schwankung
des Gasdruckes nachgibt und ein lästiges Schwanken der Brenner hervorbringt; endlich
ist der Contractionscoefficient für den Ausfluß des Gases durch die variable
ringförmige Oeffnung am Kegelventil als constant anzunehmen, wenn der Kegel sehr
spitz ist; wird dagegen ein niedriges paraboloidisches Ventil wie v angewendet, so ändert sich der Ausflußcoefficient je
nach der Stellung des Ventiles und wird um so größer, je größer die Oeffnung wird.
Dadurch wird der Vortheil erreicht, daß in dem Verhältnisse, wie der Gasconsum
wächst, mehr Gas aus dem Regulator austritt, als dem Stande des Ventiles bei
constantem Coefficienten entsprechen würde, wodurch die Druckabnahme in den
Leitungsröhren rasch wieder ausgeglichen wird. Damit das Ventil v die Oeffnung o vollständig
verschließt, wenn kein Gasconsum stattfindet, hat die Schwimmerglocke D an sich ein so geringes Gewicht, daß sie sich bei dem
höchsten vorkommenden Drucke höher als nöthig stellt; dadurch, daß man Wasser in sie
einfüllt, macht man dann ihr Gewicht gerade so groß, daß ein vollständiger Schluß
stattfindet, wenn kein Gasconsum stattfindet, aber daß die Glocke sich sofort senkt
und das Ventil öffnet, wenn durch Gasverbrauch eine Druckverminderung in den
Leitungsröhren C stattfindet. Will man später den
normalen Gasdruck abändern, so braucht man nur die Differenz des Wasserniveau's bei
x und x' zu verändern,
was sehr leicht und selbst während des Gasausflusses geschehen kann.
Die Glocke wird von oben nach unten gezogen einerseits durch ihr Gewicht P (einschließlich des in ihr enthaltenen Wassers) und
andererseits durch den Gasdruck, der auf die Oberseite des Ventiles v wirkt. Bezeichnet man den Querschnitt dieses Ventiles
in Quadrat-Decimetern mit s und den Druck des
Gases in Decimetern Wassersäule mit h, so sind die von
oben nach unten auf die Glocke wirkenden Kräfte = P +
hs Kilogrm.
Dagegen wirken auf die Glocke von unten nach oben folgende Kräfte: 1) der Druck des
Gases auf ihren inneren Querschnitt πr₃², der also = πr₃²h ist; 2) der Druck
des Gases, das mit dem Wassersäulendrucke = H zuströmt,
auf die untere Seite des Ventiles v, der also = HS ist, und 3) der Druck des Wassers auf ihre
untere Fläche, der, wenn der äußere Glockenhalbmesser mit r₄ und die Höhe der drückenden Wassersäule in Decimetern mit a bezeichnet wird, = π (r₄² – r₃²) a ist, so
daß also die gesammten von unten nach oben auf die Glocke wirkenden Kräfte = πr₃² h + HS + π (r₄² – r₃²) a, sind. Für den
Gleichgewichtszustand gilt daher die Gleichung:
πr₃² h + HS + π (r₄²
– r₃²) a = P + hs .
. . . . . . . 1)
Die Höhe des Regulirungsventiles läßt sich nun auf folgende Weise ermitteln. Ist x die Entfernung des Bodens der Glocke von dem des
Behälters A, der Halbmesser des letzteren = r₅ und der des verticalen Rohres C = r₂, so hat man,
da das Volumen des im Apparat enthaltenen Wassers constant ist (der Einfachheit
wegen unter der Voraussetzung, daß der Cylinder A etc.
vollkommen cylindrisch und nicht von der in der Figur angenommenen Form sey),
π (r₅² – r₄²)
a + π (r₃² – r₂²)(a – h) + π (r₅² – r₂²) x = V . . . . . . . . 2)
und darnach
Textabbildung Bd. 187, S. 42
Setzt man diesen Werth für a in 1) ein und entwickelt
daraus x, so erhält man
Textabbildung Bd. 187, S. 42
(Unsere Quelle gibt, wohl in Folge eines Rechnungsfehlers, die Formel
Textabbildung Bd. 187, S. 42
Es nimmt also x mit h ab und
zu; wenn man in 3) h = 0 setzt, so erhält man den Werth
von x, der dem vollständig geschlossenen Ventil
entspricht und wenn man h = H setzt, so erhält man den Werth von x für
vollständige Oeffnung. Die Differenz beider Werthe ergibt den Hub der Glocke, also
die Höhe des Regulirventiles. (Deutsche Industriezeitung, 1867, Nr. 46.)
Tafeln