| Titel: | Theoretische und praktische Untersuchungen über den Perret'schen Wasserdruck-Motor; von Ordinaire de Lacolonge. |
| Fundstelle: | Band 184, Jahrgang 1867, Nr. XVIII., S. 81 |
| Download: | XML |
XVIII.
Theoretische und praktische Untersuchungen über
den Perret'schen
Wasserdruck-Motor; von Ordinaire de Lacolonge.
Aus den Annales du Conservatoire des arts et métiers, 1866, t. VI p. 645
übertragen und bearbeitet von G.
Delabar.
Mit Abbildungen auf Tab.
III.
Perret's Wasserdruck-Motor.
Die Mittheilung unserer Quelle betrifft zunächst eine kurze Beschreibung des neuen
Motors, sodann eine Theorie über die mechanische Wirkungsweise desselben, hierauf
die damit vorgenommenen Bremsversuche und schließlich eine Prüfung der hierbei
erlangten Versuchsresultate. In dieser Ordnung sollen nun auch diese einzelnen
Punkte nacheinander betrachtet werden.
Beschreibung des neuen
Wasserdruck-Motors.
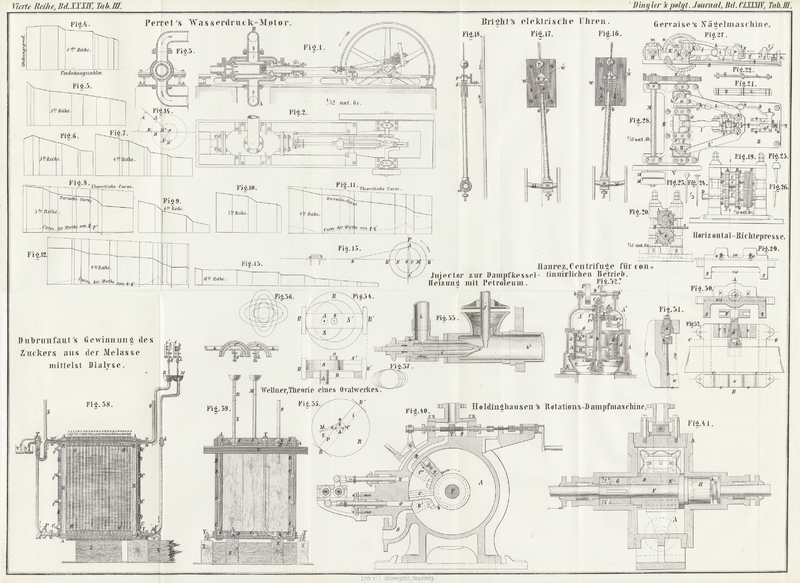
Der neue Wasserdruck-Motor des Civil-Ingenieurs F. E. Perret, wovon Fig. 1 einen
Längenschnitt, Fig.
2 einen Grundriß und Fig. 3 einen Querschnitt
zeigt, besteht aus folgenden Haupttheilen:
1) Aus einem Cylinder von Bronze, der gleichsam als Pumpenstiefel dient, worin ein
Kolben sich bewegt, auf welchen das Wasser bald auf der einen, bald auf der anderen
Seite – wie der Dampf in einer Dampfmaschine oder die erhitzte Luft in einer
doppeltwirkenden Heißluftmaschine – wirkt und ihm dadurch eine hin-
und hergehende Bewegung ertheilt.
2) Aus einer doppelten cylindrischen Umhüllung von Gußeisen, deren abgerundete Enden
sich auf beiden Seiten an den Pumpenstiefel oder den Arbeitscylinder, welcher sich
selbst wieder in ihnen, sammt dem Kolben, hin- und herbewegt, dicht
anschließen. Die eine dieser Umhüllungen, und zwar die innere, ist in Verbindung mit
der oberen oder der Zuflußröhre, und die andere äußere mit der unteren oder
Abflußrohre. Daß der Arbeitscylinder sowohl innen als außen auf das Sorgfältigste
abgedreht und adjustirt seyn muß, versteht sich von selbst. Dasselbe gilt auch für
die ihn berührenden Mantel- und Kolbenflächen, zwischen welchen er sich, wenn die
Maschine in Thätigkeit ist, hin- und herbewegen muß.
Um abwechselnd beide Seiten des Arbeitscylinders mit der einen oder anderen der
beiden Umhüllungen in Verbindung zu setzen, ist derselbe gegen seine Enden hin mit
einer Reihe von Oeffnungen durchbrochen, welche der Flüssigkeit bei der
abwechselnden Hin- und Herbewegung des Cylinders in denjenigen Stellungen, in
welchen sie mit den Höhlungen der Gußmäntel in Verbindung stehen, den Ein-
und Austritt gestatten.
Diese Oeffnungen oder Löcher nehmen nicht den ganzen ringförmigen Umkreis des
Cylinders ein, sondern lassen volle oder massive Stellen zwischen sich, wodurch die
Enden mit dem mittleren Hauptkörper zusammenhängen.
Um die Bewegung des Kolbens im Arbeitscylinder oder Pumpenstiefel hervorzubringen,
genügt es, die Oeffnungen des Cylinders selbst in eine solche Lage zu versetzen, daß
die Flüssigkeit auf der einen Seite durch die obere oder Druckleitung ankommen und
auf der anderen durch die untere oder Ableitung wieder entweichen kann, und daß
hernach, wenn der Kolben am einen Ende seines Laufes angelangt, die Verbindung der
Oeffnungen und damit auch die Wirkung des Wassers sich umkehre, so daß der Kolben
nach der entgegengesetzten Seite bewegt wird.
Weil die Oeffnungen beim Spiele des Motors sich hin- und herbewegen müssen, so
ist es, wie bereits bemerkt, unumgänglich nöthig, daß der Arbeitscylinder selbst
diese Bewegung mitmache. Diese Steuerungsbewegung wird durch folgende Anordnung
erlangt: Auf der unter rechtem Winkel gekröpften Treibwelle, welche vom
Arbeitskolben aus mittelst der Treibstange und Kurbel in Umdrehung versetzt wird,
ist, außer dem Schwungrad zur Regulirung der Bewegung, zur Seite ein Excentric
aufgesetzt, dessen Stange am anderen Ende mit einem Halsband verbunden ist, das die
dießseitige Verlängerung des Pumpenstiefels umgibt und diesen bei der hin-
und hergehenden Bewegung des Excentrics mitnimmt.
Durch diesen Steuerungs- oder Vertheilungsmechanismus unterscheidet sich der
Perret'sche Motor auch von der Wassersäulenmaschine,
mit der er sonst einige Aehnlichkeit hat.
Die Einrichtung des neuen Motors ist, wie man sieht, in theoretischer Hinsicht sehr
einfach; indessen bot sie in der praktischen Ausführung gleichwohl manche
Schwierigkeiten dar. Da nämlich das Wasser nur sehr wenig Zusammendrückbar ist, so
ist es nöthig, daß im Moment, in welchem der Zufluß aufhört, der Abfluß auch schon
wieder begonnen hat. Die Flächen, welche bei jedem Hub die Oeffnungen für einen
Augenblick bedecken, müssen deßhalb sehr genau einsprechen, und wie der ganze Arbeitscylinder und
Steuerungsmechanismus sehr genau gearbeitet seyn. Darin besteht denn auch der
schwierigste Theil des neuen Apparates. Andere Uebelstände werden im Verlaufe der
Untersuchung noch zur Sprache kommen.
Diesen Schwierigkeiten gegenüber besitzt die Maschine von Perret aber auch ihre Vortheile, und um diese wie jene richtig beurtheilen
und gegen einander abwägen zu können, müssen wir uns nun vor Allem mit der
Wirkungsweise und der Leistungsfähigkeit des neuen Motors vertraut machen.
Theorie der mechanischen Wirkungsweise
des Motors.
Bei diesem Motor hängen die Verluste der lebendigen Kraft oder Nutzwirkung von
folgenden drei allgemeinen Ursachen ab:
1) von den Anordnungen, welche zur Zuleitung des Wassers in den
Cylinder dienen;
2) von der speciellen Einrichtung des Motors selbst;
3) von der Bewegung der beweglichen Theile.
Die Versuche der ersten Art variiren für jeden besonderen Fall mit den Details der
Leitung. Diejenigen, welche von den Formen des Motors abhängen, sind durch Formeln
ausgedrückt, welche sich für dieselbe Maschine nicht ändern. Die Verluste der
dritten Art lassen sich für gewisse Organe leicht berechnen; aber für andere,
glücklicherweise minder wichtige Mechanismen ist die Rechnung aus Mangel an
bekannten Erfahrungen oder anderen hinreichenden Daten zum Schätzen der Widerstände
beinahe unmöglich.
Bezeichnen wir durch:
H' die Höhe des Wasserspiegels im oberen Reservoir über
dem Mittelpunkte der Oeffnung, durch welche die Flüssigkeit in die Zuleitung
eintritt; H'' die verticale Entfernung dieses Punktes
bis zu der horizontal vorausgesetzten Maschinenachse;
H''' diejenige von der Achse bis zum Niveau des unteren
Bassin, wobei angenommen wird, daß der Durchmesser des Kolbens in Bezug auf H' + H'' sehr klein sey; H = H' + H'' + H''' das totale
Gefälle;
D den Durchmesser der cylindrisch gedachten
Zuleitung;
Ω = πD²/4 ihren Flächeninhalt und
L ihre Länge;
U die Geschwindigkeit des Wassers in dieser
Zuleitung;
p die ganze Länge der Oeffnungen auf einer Seite des
Pumpenkörpers, gemessen auf dem mittleren Umfang des Cylinders,
l ihre Breite, welche auch die Hälfte ihres Laufes
ist;
Ω ₁ = 1/2 pl
den mittleren Inhalt dieser Oeffnungen;
U ₁ die mittlere Geschwindigkeit, mit welcher das
Wasser diese Oeffnungen durchfließt;
D ₂ den inneren Durchmesser des Pumpenstiefels,
welcher zugleich auch derjenige des Kolbens ist;
Ω ₂ = πD²₂/4 seinen Querschnitt;
2 R den Lauf des Kolbens, welcher
gleich ist dem doppelten Radius der Kurbel;
U ₂ die mittlere Geschwindigkeit des Wassers in
dem Pumpenstiefel, welche zugleich auch diejenige ist, womit der Kolben bewegt
wird;
D ₃ den inneren Durchmesser der ebenfalls
cylindrisch vorausgesetzten Austrittsleitung;
Ω ₃ = πD²₃/4 ihren Querschnitt;
L ₃ ihre Länge;
U ₃ die mittlere Geschwindigkeit, mit welcher die
Flüssigkeit darin fortgeführt wird;
Q das Wasserquantum oder Wasservolumen in Kubikmetern,
welches per Secunde verbraucht wird;
Δ die Dichtigkeit des Wassers oder das Gewicht
eines Kubikmeters Wasser, welches 1000 Kilogr. beträgt;
M die dem Volumen Q
entsprechende Masse ΔQ/g;
ω die mittlere Geschwindigkeit der
Kurbelwarze;
N die Anzahl der Kurbelumdrehungen per Minute.
Da die Maschine immer mit einem Schwungrad versehen ist, so kann man ω constant oder doch periodisch gleichförmig
annehmen und folglich der Rechnung das Mittel aus den verschiedenen Werthen der
Winkelgeschwindigkeit zu Grunde legen.
Bevor wir die Berechnung der Verluste an lebendiger Kraft beginnen, wollen wir noch
auf eine Eigenthümlichkeit der Perret'schen Maschine
hinweisen, auf welche de Lacolonge von seinem Freunde,
dem Bergwerks-Ingenieur de Langlade, aufmerksam
gemacht worden ist.
Die Kurbel und das Excentric der Steuerung sind, wie bereits bemerkt, unter rechtem
Winkel auf die Treibwelle gesetzt. Setzen wir die Treibstange unendlich lang voraus,
d.h. so daß sie in allen ihren Lagen der Achse des Cylinders, welche verlängert gedacht,
die Umdrehungsachse trifft, parallel ist.
Wenn dann die Kurbelwarze in R und diejenige des
Excentrics in R' ist, Fig. 14, so ist der
Kolben am äußersten Ende (links) seines Laufes und die Oeffnungen auf dieser Seite
sind vollständig geschlossen. Wenn nun die Welle sich um den Winkel α dreht, beschreibt der Kurbelzapfen den Bogen
RA und der Kolben durchläuft in gerader Linie den
Weg
RB = R (1
– cos α) = e.
In diesem Augenblick ist die Geschwindigkeit V, mit
welcher sich die Treibstange bewegt
V = de/dα = d[R(1 – cos
α)]/dα = – R (d cos α)/dα = R sin
α.
Die Geschwindigkeit der Treibstange, also auch der Kolbenstange und des Kolbens, ist
also dem Sinus des Drehungswinkels proportional. Dasselbe gilt auch für das Volumen,
welches währenddem durch den Kolben erzeugt worden ist.
Während der gleichen Zeit bewegt sich der Mittelpunkt des Excentrics von R' nach A' und der
Pumpenstiefel von O nach B',
wobei OB' = l sin α,
also ebenfalls mit dem Sinus des beschriebenen Drehungswinkels proportional ist.
Weil die Eintrittsöffnung sich wie das vom Kolben erzeugte Volumen ändert, so muß,
damit die eingeführte Flüssigkeit dieses letztere stets füllt, die Geschwindigkeit,
womit dieselbe durch die Oeffnungen geleitet wird, constant bleiben, jedoch immer
unter der Voraussetzung einer unendlichen Treibstange.
Die Geschwindigkeit in den Leitungsröhren soll sich also ändern wie der Durchschnitt
dieser Oeffnungen, d.h. proportional dem Sinus des von der Kurbelwarze beschriebenen
Drehungswinkels. In der Wirklichkeit ist es wegen der schiefen Stellung der
Treibstange nicht absolut so; aber es ist gewiß, daß die Geschwindigkeit der
Flüssigkeit in den Zuführungs- und Abflußrohren periodisch veränderlich ist,
was dazu führt, das Mittel derselben aus den verschiedenen Werthen aufzusuchen.
Die Umfangsgeschwindigkeit findet sich aus der Anzahl N
der in einer Minute beschriebenen Umdrehungen; denn es ist
v = ωR = 2πRN/60, woraus
N = 30ω/π . . . . . . . . . . (1)
Das in einer Minute verbrauchte Volumen ist dem durch den Kolben in derselben
Zeitdauer erzeugten gleich; man hat also:
60 Q = 4 RQ₂ N, woraus
Q = RΩ₂ N/15 . . . . . (2)
Indem man die mittlere Geschwindigkeit des Kolbens mit U₂ bezeichnet, hat man aber auch:
Q = U₂ Ω₂ . . . . . . . . (3)
Durch Gleichsetzung von (3) und (2) folgt nun weiter:
U₂ Ω₂ = RΩ₂ N, woraus mit Berücksichtigung von (1)
U₂ = Q/Ω₂ = RN/15 = 2ωR/π . . . . . . . . .
. . (4)
Damit die Bewegung der Flüssigkeitsmasse continuirlich und gleichförmig erfolge,
müssen in der Zeiteinheit durch jeden Querschnitt des Apparates gleiche Volumina
gehen. In der Zu- oder Druckleitung ist dieses Volumen:
Q = ΩU . . . . . . . . . . (5)
In dieser Leitung befindet sich ein Hahn, der die gleiche Rolle wie das Schutzbret
bei den Wasserrädern versieht, und welcher wegen der Aehnlichkeit mit dem bei
Locomotiven vorkommenden Regulator ebenfalls Regulator genannt werden könnte.
Die durch diesen Hahn in irgend einem Augenblick freigelassene Durchlaßöffnung kann
zum Querschnitt der Leitung in einem festgesetzten Verhältniß 1/m stehen, wobei m meist
größer, aber auch kleiner als 1 seyn kann. Im ersten Fall entsteht durch die
Hahnöffnung eine Verengung, im zweiten eine Erweiterung.
Indem wir daher mit u die Geschwindigkeit des Wassers
beim Durchgang durch die Hahnöffnung bezeichnen, erhalten wir allgemein:
u = mU.
Der mittlere Querschnitt der Oeffnungen auf einer Seite des Pumpenstiefels ist:
Ω₁ = 1/2 pl,
und für das mittlere Volumen der Flüssigkeit, welche durch
dieselben fließt, hat man:
Q = Ω₁ U₁ . . . . . . . . . .
(6)
Für die Ausflußröhre hat man ebenso:
Q = Ω₃ U₃ . . . . . . . . . .
(7)
Indem man in den Gleichungen (3), (5), (6) und (7) für Ω, Ω₁, Ω₂
und Ω₃ ihre Werthe setzt, nämlich:
Ω = πD²/4; Ω₁ = 1/2 pl; Ω₂ = πD²₂/4; Ω₃ = πD²₃/4,
erhält man die folgenden Werthe für die verschiedenen
Geschwindigkeiten:
Textabbildung Bd. 184, S. 87
welche, wie man sieht, durch U₂, die Geschwindigkeit des Kolbens, ausgedrückt sind, und es daher
möglich machen, alle Verluste an lebendiger Kraft als Functionen der
Kolbengeschwindigkeit U₂, oder, was dasselbe
sagt, als Function der Umdrehungszahl N zu
berechnen.
Beginnen wir nun zuerst mit jenen Verlusten, welche in den Leitröhren
stattfinden:
Jedesmal, wenn eine Flüssigkeit – unter dem Einfluß einer
Niveau-Verschiedenheit oder eines Druck-Ueberschusses – sich
von einem Gefäß in ein anderes begibt, indem sie durch eine Oeffnung vom Querschnitt
S geht, so differirt der wirkliche Ausfluß vom
theoretischen in einem Verhältniß, welches mit den Anordnungen der Oeffnung sich
ändert. Nennen wir allgemein q die theoretische
Ausflußmenge dieser Oeffnung und v₁ die
Geschwindigkeit, mit welcher sie durchfließen würde, so hat man:
q = Sv₁;
statt dessen hat man aber in Wirklichkeit ein verschiedenes
und zwar immer ein kleineres Volumen, welches ausgedrückt wird durch:
q' = μSv₁.
Hierbei ist μ der Ausflußcoefficient, eine Zahl,
die zwischen 0,95 und 0,60 variirt, je nachdem die Kanten der Ausflußöffnung mehr
oder weniger abgerundet sind. Es ist oft schwer, die Geschwindigkeit v₁ zu bestimmen, während das directe Messen des
ausgeflossenen Wassers es ermöglicht, die Ausflußgeschwindigkeit v₂ zu kennen, welche also gibt:
v₂ = μv₁, woraus folgt:
v₁ = v₂/μ.
Indem man dieses auf den vorliegenden Fall anwendet, findet man, daß der Verlust an
lebendiger Kraft, welchen die Masse M erleidet, indem sie vom oberen
Reservoir in die Druckleitung mit der Geschwindigkeit U
übergeht, seyn wird:
M (1/μ – 1)² U² = M (1/μ –
1)² U⁴₂/D⁴ .
U²₂ = MaU²₂ . . . . (9)
wenn anders (1/μ –
1)² D⁴₂/D⁴ zur Einfachheit mit a bezeichnet
wird.Da die lebendige Kraft L allgemein durch: L = 1/2 Mv²
ausgedrückt wird, so müßte eigentlich der vorige Ausdruck in (9), wie auch
die folgenden in (10) bis (22) mit 1/2 multiplicirt seyn, wie dieß später in
der Gleichung (26) des Nutzeffectes geschehen ist.
Die Bewegung der Flüssigkeit in dieser Leitung ruft noch andere Widerstände hervor,
welche ihrer Länge L und ihrem Umfang πD direct und ihrem Querschnitt Ω = πD²/4 indirect proportional sind, so daß, wenn β ein constanter Erfahrungscoefficient ist,
welchen man im Mittel zu 0,0032 annehmen kann, der Verlust an lebendiger Kraft durch
diese Widerstände ausgedrückt wird durch:
4 Mβ L/D . U² = 4 MβL
D⁴₂/D⁵ . U²₂ = MbU²₂ . . . . . (10).
Die Verengung, resp. Erweiterung des Wasserstrahles beim Durchgang durch die Hähne
verursacht den dritten Verlust an lebendiger Kraft, welcher sich wie der erste
berechnen läßt, und demnach ausgedrückt wird durch:
M (u
– U)² = M (m – 1)² . D⁴₂/D⁴ . U²₂ = McU²₂ . . . . (11)
In Folge der Geschwindigkeitsänderungen in der Leitung brachte Perret auf derselben ein Luftreservoir an, dem Windkessel ähnlich, wie man
ihn über der Steigröhre der Druckpumpe, besonders bei Feuerspritzen, anbringt. Es
entsteht daraus in gewissen Zeitmomenten ein Verlust an lebendiger Kraft, den man
aber, da die Luft, in Folge ihrer Elasticität, denselben in anderen Zeitmomenten
wieder ersetzt, vernachlässigen kann.
Die Verluste, welche in dem Maschinenkörper stattfinden, sind folgende:
Zuerst gehört dahin jener, welcher durch die Verengung beim Eintritt in die
Oeffnungen verursacht wird, dessen Ausdruck ist:
M (U
– U₁)² = M (D²₂/D² – πD²₂/2pl)² . U²₂ = MdU²₂ . . . (12)
Sodann entsteht ebenso durch die Erweiterung der Flüssigkeit beim Austritt aus den
Oeffnungen in den Pumpenstiefel ein Verlust, der ausgedrückt wird durch:
M (U₁ – U₂)² = M (πD²₂/2pl –
1)² U²₂ = MiU²₂ . . . . (13).
Beim Uebergang des Wassers aus dem (Minder durch die Austrittsöffnungen entsteht
durch die Zusammenziehung des Wassers ein neuer Verlust, der ausgedrückt wird
durch:
M (U₂ – U₁)²,
und welcher, wie man sieht, dem vorigen gleich ist, weßhalb
dieser zweimal zu nehmen ist.
Die Verluste, welche von den Widerständen in der Abflußleitung herrühren, finden sich
auf gleiche Weise, wie jene, die sich auf die Zuleitung beziehen. Dieselben werden
daher ausgedrückt durch:
4 Mβ L₃ /D₃ . U²₃ = 4 MβL₃ D⁴₂/D⁵₃ U²₂ = MnU²₂ . . . . . (14).
Noch andere Verluste entstehen aus der Richtungsänderung, welche das Wasser auf
seinem Wege durch die Zu- und Ableitung und durch die Maschine erleidet.
In einem solchen Falle ist die anzuwendende Formel:
M (0,0039 + 0,0186r) e/r² . u'² . . . . . (15)
in welcher bezeichnet:
r den Radius des mittleren Umkreises, durch welchen sich
die Flüssigkeit bewegt;
e die Länge des Bogens, welchen sie während dieser Zeit
beschreibt;
u' die Geschwindigkeit, mit welcher die Bewegung vor
sich geht.
Im vorliegenden Falle ist zunächst für die knieförmige Ablenkung in der Zuleitung die
Geschwindigkeit U, der durchlaufene Bogen ein
Viertelkreis, also e = πr/2. Man wird also haben:
e/r² = πr/2r² = π/2r, und die obige Formel (15)
ändert sich in: M (0,0039 + 0,0186. r) π/2r . U² oder nach
(8):
M (0,0039 + 0,0186 . r) π/2r . D⁴₂/D⁴ . U²₂ . . . . . . (16).
Indem die Flüssigkeit vom Vertheilungsmantel in die Oeffnungen und von diesen in den
Cylinder eintritt, beträgt der Ablenkungswinkel 2 . 90 = 180° und ist die Geschwindigkeit der
durchströmenden Flüssigkeit U₁. Bezeichnet man
daher den Radius der entsprechenden Ablenkungsbogen mit r' und letztere mit e' = πr', so ist: e/r² = π/r', und
der entsprechende Verlust ist:
M (0,0039 + 0,0186 . r') π/r' . π² D⁴₂/4p² l² . U²₂ . . . . (17).
Beim Austritt aus dem Cylinder durch die Oeffnungen in den äußeren Mantel hat die
Flüssigkeit dieselbe Ablenkung von 2 . 90 = 180° zu durchlaufen. Bezeichnet
man also den mittleren Radius der Ablenkungsbogen mit r'' und die Geschwindigkeit wieder mit U₁, so ist der entsprechende Verlust an lebendiger Kraft:
M (0,0039 + 0,0186 . r'') π/r'' . πD⁴₂/4p² l² . U²₂ . . . . (18).
Um von dem äußeren Mantel in die Austrittsröhre zu gelangen, hat das Wasser nochmals
einen rechten Winkel in einem Bogen vom Radius r''' mit
einer Geschwindigkeit U₃ zu durchlaufen, und
erleidet in Folge dessen einen Verlust an lebendiger Kraft, welcher ausgedrückt wird
durch:
M (0,0039 + 0,0186 . r''') π/2r''' . D⁴₂/D⁴₃ . U²₂ . . . . (19).
Bei den numerischen Rechnungen ist es bequemer, die Summe der Ausdrücke (17) und (18)
zusammenzufassen, was gibt:
Textabbildung Bd. 184, S. 90
Ebenso kann man auch die Ausdrücke (16) und (19) zusammennehmen und erhält dafür:
Textabbildung Bd. 184, S. 90
Diese Formel wird die Rechnung namentlich in dem Falle erleichtern, wenn die
Ausflußröhre denselben Durchmesser wie die Zuleitungsröhre hat, d.h. wenn D = D₃ ist; dafür
verwandelt sie sich in:
Textabbildung Bd. 184, S. 90
In allen anderen Fällen wird es aber ebenso einfach seyn, die Formeln (16) und (19)
anzuwenden. Uebrigens hat Perret wirklich bei allen
Maschinen, die er bis jetzt ausführte, D = D₃ gemacht; also wird man sich in den
nachfolgenden Zahlen-Rechnungen wirklich der Formel (21') bedienen
müssen.
Endlich ist die lebendige Kraft, welche das Wasser bei seinem Austritt aus der
Ausflußröhre noch in sich enthält, für den Nutzeffect ebenfalls verloren. Dieser
Verlust ist:
MU²₃ = M (D⁴₂/D⁴₃) . U²₂ = MtU²₂ . . .
(22).
Die Summe aller dieser verschiedenen Verluste an lebendiger Kraft, welche die
Flüssigkeit bei ihrem Laufe durch die Maschine und die Zu- und Ableitungen in
Folge der verschiedenen Bewegungshindernisse erleidet, wird also seyn:
M (a +
b + c + d + 2i
+ o + q + s + t) U²₂ = MAU²₂.
Die Größen in der Klammer sind Functionen der Dimensionen des Apparates und der
festgesetzten Coefficienten. Ist der Durchmesser der Zu- und Ableitung
derselbe, also D = D₃, so ist, wie oben bemerkt, s durch s' zu ersetzen. Die ganze Summe ist durch A dargestellt.
Es bleibt nun noch übrig, die Arbeits- oder Wirkungsgrößen zu berechnen,
welche durch die passiven Widerstände absorbirt werden.
Der Umfang des Kolbens, welcher mit einer doppelten Lederdichtung versehen, ist π
D₂; die Höhe dieser Liderung sei E, also die Berührungsfläche derselben mit der inneren
Cylinderwand = π
D₂ E. Der Weg, den
der Kolben in der Secunde zurücklegt, also die Geschwindigkeit, ist U₂. Der Druck, welcher auf den Kolben wirkt und
somit auch die Liderung an die Cylinderwand drückt, entspricht dem Gewicht einer
Wassersäule von der Dichtigkeit Δ und der Höhe
(H' + H''). Der
Reibungscoefficient endlich sey f. Dieß Alles
vorausgesetzt, ist die durch die Kolbenreibung absorbirte Arbeit:
fπD₂ EΔ (H' + H'') U₂ . . . .
(23),
oder, wenn man für U₂
seinen Werth aus (4) substituirt, nämlich: U₂ =
Q/Ω₂ =
4Q/πD²₂ und berücksichtigt, daß ΔQ = Mg, worin g die Beschleunigung der
Schwere bedeutet, so verändert sich der vorige Ausdruck in:
Mg (4fE/D₂) (H'
+ H'') . . . . . (24).
Indem man durch ρ den Radius der Zapfen der
Treibwelle, durch f' den Reibungscoefficienten der
Achsenreibung und durch K das Gewicht des Schwungrades
bezeichnet, ist die durch die Achsenreibung consumirte Arbeit per Secunde:
2πρf'KN/60,
ein Ausdruck, der auf analoge Art wie im vorigen Falle
verwandelt werden kann in:
Mg . (2ρKf')/(ΔD²₂ R) . . . . . . (25).
Es gibt nun zwar noch andere Maschinentheile, deren Bewegung eine gewisse
Arbeitsgröße consumirt, wie z.B. das Gleiten der Führungsstange bei der Geradführung
der Kolbenstange, die Drehung des Kurbelzapfens in dem Treibstangenkopf, die
hin- und hergehende Bewegung des Cylinderkörpers in seiner Umhüllung, und die
Drehung des Vertheilungsexcentrics in seinem Halsband. Bei allen diesen Bewegungen
finden Reibungswiderstände statt, denen gewisse Arbeitsverluste entsprechen, die
sich ebenfalls wie die obigen berechnen ließen. Die einen derselben sind aber so
unwichtig, daß man sie vernachlässigen kann, und behufs der Beurtheilung der anderen
müßte man Kräftezerlegungen vornehmen, welche in der Adjustirung der Theile eine
mathematische Genauigkeit voraussetzen, die nicht bestehen würde, so daß die
Ergebnisse der Rechnung jedenfalls bedeutend von der Wirklichkeit differiren müßten.
Man hat daher auch über diese Verluste keine Rechnungen angestellt und sie bei den
folgenden Rechnungen nicht weiter berücksichtigt.
Nach dem Princip der lebendigen Kräfte kann man also setzen:
Textabbildung Bd. 184, S. 92
Dieß ist nun die Gleichung für die disponible Arbeit per Secunde oder den Nutzeffect. P ist das Auflegegewicht auf der Waagschale des
Bremshebels in Kilogrammen und v die Geschwindigkeit des
Aufhängepunktes derselben in Metern. Der Nutzeffect Pv
ist somit in Kilogrammmetern ausgedrückt.
Indem man auf beiden Seiten der vorigen Gleichung mit MgH, der totalen Arbeit oder dem absoluten Effect, theilt, verwandelt sich
dieselbe in folgende Formel:
Textabbildung Bd. 184, S. 92
worin das Glied auf der linken Seite das Verhältniß der disponibeln zur totalen Arbeit, oder des Nutzeffectes zum absoluten Effect ausdrückt. Dieses
Verhältniß heißt auch der Wirkungsgrad oder die Leistungsfähigkeit. Deßhalb drückt die vorige Formel die Gleichung des Wirkungsgrades oder der Leistungsfähigkeit aus. Unter dieser
Form ergeben sich leicht folgende Schlüsse:
In einer bestimmten Maschine ist das Verhältniß der durch die
Zapfen consumirten Arbeit zur absoluten Arbeit des Motors für ein gegebenes
Gefälle constant, wie auch die Umdrehungsgeschwindigkeit seyn mag.
Ebenso ist auch das Verhältniß der durch den Kolben
consumirten Arbeit zur absoluten Arbeit des Motors constant, wie auch die
Umdrehungsgeschwindigkeit sey, sofern anders das Verhältniß (H' + H'')/H
constant ist, d.h. die Maschine bei einem gegebenen Gefälle
ihre gleiche Lage der Aufstellung behält.
Dieses letztere Verhältniß ist um so geringer, je näher dem
Niveau des oberen Reservoirs die Maschine angebracht ist. Denn alsdann ist
der Zähler des Bruches (H' + H'')/H und damit auch das entsprechende Glied
der Kolbenreibung kleiner. Damit dieß so sey, muß aber die Ausflußröhre denselben
Durchmesser wie die Zuleitungsröhre haben, weil sonst im ersten Falle die
Widerstände per laufenden Meter stärker wären als im
zweiten Falle, was das Ergebniß verringern würde.
Die Arbeitsverluste, welche den verschiedenen Widerständen
entsprechen, die das in Bewegung gesetzte Wasser während seines Laufes durch die
Maschine und die Zu- und Ableitung erleidet, sind für ein gegebenes
Gefälle um so kleiner, je kleiner die Geschwindigkeit des Kolbens oder die
Umdrehungszahl per Minute ist.
Indem man die Umdrehungszahlen als Abscissen und die Ergebnisse für den Wirkungsgrad
oder die Leistungsfähigkeit als Ordinaten annimmt, erhält man eine Curve, welche
eine Parabel ist, deren Scheitel auf der Ordinatenachse y liegt und zwar in einer Höhe, die durch die Größen:
Textabbildung Bd. 184, S. 93
ausgedrückt ist.Denn für N = 0 ist auch U₂ und damit in (27) auch das Glied A . U²₂/2gH gleich Null.
Dieser Werth gibt zugleich die obere Grenze des Ergebnisses an, welche man indessen,
da die Kolbengeschwindigkeit natürlich nie Null werden kann, niemals erreichen kann,
welcher man sich aber um so mehr nähert, je kleiner U₂ wird, je langsamer also der Kolben sich bewegt. Dieß zeigt, daß das Ergebniß des neuen Motors kein relatives Maximum
zuläßt, daß es aber von Vortheil ist, die Maschine mit geringer Geschwindigkeit
gehen zu lassen.
Außer diesen Schlüssen über den Lauf einer bestimmten Maschine kann man aus den bis
jetzt aufgestellten Gleichungen auch noch Folgerungen ziehen, die sich auf die
Construction solcher Maschinen beziehen. Aus der obigen Gleichung (11) ist sogleich
zu sehen, daß ein Hahn, dessen Querschnitt größer oder kleiner als jener der
Röhrenleitung ist, keinen Vortheil darbietet, im Gegentheil einen entsprechenden
Effectverlust nach sich zieht, und daß es daher vorzuziehen ist, daß die
Querschnitte der Hahnöffnung und der Röhrenleitung gleich seyen.
Der Ausdruck in Gleichung (12) bezüglich der Contraction des Wassers beim Eintritt in
die Oeffnungen des Pumpenstiefels wird Null, wenn 2 pl =
πD², oder pl = 2 . πD²/4, d.h. wenn der Querschnitt der Oeffnungen doppelt so groß ist als
der Querschnitt der Zuleitungsröhre.Um dieß besser einzusehen, bringe man den Ausdruck (12) auf die Form:Textabbildung Bd. 184, S. 94denn dann ist für 2 pl =
πD² der Quotient 2 pl/πD² = 1, also der Factor (2pl/πD²
– 1) = 0. Diese Bedingung ist nicht schwer zu erfüllen, weil die Oeffnungen auf einem
Cylinderumfang sich befinden, was ihnen eine kleine Breite zu geben gestattet.
Indessen wird es in Wirklichkeit in diesen Oeffnungen immer Verluste geben, selbst
in diesem günstigsten Falle, weil es während einem Theil der Einführung immer
Verengungen und während dem anderen Erweiterungen gibt, die jene Verluste nach sich
ziehen. Perret macht darum gewöhnlich pl = πD², oder
pl = 4 . πD²/4, d.h. die Summe der Oeffnungen
gleich dem vierfachen Inhalt des Querschnitts der Zuflußröhre.
Ferner ist es immer vortheilhaft, die Ränder der Oeffnung des
Reservoirs, von welcher die Druckleitung ausgeht, abzurunden, denn dadurch wird der Ausflußcoefficient μ
vergrößert, also in (9) der Factor (1/μ – 1) vermindert.
Derselbe Ausdruck, sowie auch die Ausdrücke (10) und (16) sind numerisch um so kleiner, je kleiner
U, die Geschwindigkeit des Wassers
in der Zuleitung, oder je größer der Durchmesser
D
der letzteren ist.
Die Ausdrücke (19), (21) und (22) zeigen ebenso, daß es um so
vortheilhafter ist, je kleiner die Geschwindigkeit
U₃ der Ausflußleitung, je
größer also der Durchmesser
D₃ dieser Leitung
ist.
Es ist bereits oben bemerkt worden, daß, wenn D₃ =
D gemacht wird, der Vortheil
erlangt werde, den Motor in einer beliebigen Höhe der Zuleitung (die jedoch
kleiner als 10,30 Met. seyn muß) aufstellen zu können, ohne
die Verluste an lebendiger Kraft zu vermehren. Man wird also dieses
Verhältniß, wie es auch Perret gethan, annehmen.
Indem manU₁ = U₂ annimmt, d.h. indem man den Querschnitt des Pumpenstiefels dem
mittleren Inhalt der Oeffnungen auf einer Seite desselben gleichmacht,
verschwindet der auf die Erweiterung bezügliche Verlust des Receptors.
Dieser Umstand wird sich indessen nicht immer vorfinden, weil die Geschwindigkeit in
den Oeffnungen des Pumpenstiefels ungefähr constant ist, während jene des Kolbens,
wie wir im Anfange gesehen haben, sich nach dem Sinus des Drehungswinkels
ändert.Da der Sinus bei kleinerem Winkel schneller wächst als bei größerem, so
verändert sich auch die Geschwindigkeit des Kolbens am Anfang und Ende
seines Laufes stärker als in der Mitte seines Hubes.
Die Ausdrücke (17) und (18) zeigen, daß bei gleichem Durchgang und gleichem Radius
der Krümmung die der Richtungsänderung entsprechenden Verluste
um so geringer ausfallen, je kleiner die Geschwindigkeit in den
Durchgangsöffnungen ist oder je größer ihr Querschnitt ist.
Endlich sind die von der Kolben- und Zapfenreibung
herrührenden Verluste (24) und (25) um so kleiner, je
größer der Durchmesser des Pumpenkörpers ist. Perret macht gewöhnlich D₂ = D, d.h. den
Durchmesser des Pumpenstiefels gleich dem Durchmesser der Zuleitung.
Aus Allem dem ergibt sich, daß es vortheilhaft ist, den
Durchmesser der Röhrenleitungen und des Arbeitscylinders so groß zu nehmen, als
es die Bedingungen des Baues der Maschine gestatten.
Bremsversuche, welche mit dem neuen
Motor angestellt wurden.
Der Wasserdruck-Motor, wie er im Anfange dieses Artikels beschrieben wurde und
in den Figuren
1, 2
und 3 im
Längenschnitt, Grundriß und Querschnitt dargestellt ist, ist das erste von Perret gebaute derartige Modell. Dieser Motor war der
Gegenstand von Versuchen, deren Resultate in folgender Tabelle zusammengestellt
sind. Damit hat man die Konstanten erhalten, vermittelst deren die nachfolgenden
Rechnungen ausgeführt worden sind.
Der Bremshebel war 2 Met. lang und ist in Bezug auf die Achse der Treibwelle, auf
welche er gesetzt war, zum Voraus äquilibrirt worden.
Indem man die Anzahl der Umdrehungen per Minute wie
früher mit N und die Geschwindigkeit des Aufhängepunktes
für die Waagschale am Zaum mit V bezeichnet, ist:
V = (2π . 2 . N)/60 = πN/15 = 0,2094395 . . . . . . . (28).
Der Kolbenlauf ist: 2 R = 0,24 Met. und folglich die
mittlere Geschwindigkeit v des Kolbens ebenfalls per Secunde:
v = (2 . 2R . N)/60 = RN/15
= 0,008 . N . . . . . . (29).
Der Querschnitt des Cylinders, dessen Durchmesser D₂ = 0,08 Met., ist: Ω₂ = πD²₂/4 = (π . 0,08²)/4, und folglich das vom
Kolben per Secunde erzeugte Volumen:
Q' = Ω₂v = (π . 0,08²)/4 . 0,008 . N =
0,0000402124. N . . . . . . (28).
Die damit erhaltenen Rechnungsresultate sind ebenfalls in der folgenden Tabelle
zusammengestellt und zugleich durch die Diagramme der Figuren 4–12, worin die
Anzahl der Umdrehungen als Abscissen und die Ergebnisse des Wirkungsgrades als
Ordinaten angenommen, dargestellt.
Tabelle über die verschiedenen
Versuchsreihen, welche mit Perret's
Wasserdruck-Motor in Bordeaux und Arcachon angestellt wurden.
Textabbildung Bd. 184, S. 97
Nr. der Versuche; Gewicht der per Sec. verbrauchten Wassermenge ΔQ;
Gefälle, bis zur Treibachse gemessen H'; Totales Gefälle H; Totale Arbeitsgröße
von ΔQH' ΔQH; Anzahl der Umdrehungen per Minute N; Geschwindigkeit
des Bremshebels per Sec. V = 0,2094395 N; Gewicht auf der Waagschale P;
Nutzeffect PV; Ergebniß des Wirkungsgrades; PV/ΔQH' PV/ΔQH';
Theoretisches Ergebniß des Wirkungsgrades; Volumen welches v. Kolben erzeugt
wird. Q' = 0,0000402124 N; Differenz von Q – Q'; Kolbengeschwindigkeit
per Sec. v = 0,008 N; Versuche im Bahnhof „Ségur“ zu
Bordeaux.; Versuchsreihe; Die Zuleitung hatte einen Durchmesser
von 0,08 Met.; der Hahn einen Querschnitt, der gleich 8/5 von jenem der Röhre;
das Schwungrad wiegt 52,70 Kil.; die Maschinenachse ist 0,96 Met. über dem
Bassin, in welches die 0,08 Met. weite Röhre eintaucht, durch die das Wasser
entweicht, welches den Kolben bewegt hat.; Kil.; Met.; Lit.;
Dieselben Anordnungen wie vorhin, ausgenommen daß das untere Ausflußrohr
weggehoben wurde und das Wasser vom Cylinder frei in die Luft fiel
1) Im Anfang der Versuchsreihe war der Gang sehr sanft, hernach
gab es im Cylinder Stöße, welche um so merklicher wurden, je größer die
Umdrehungsgeschwindigkeit war. 2) In dieser Reihe waren die Stöße weniger stark und
fiengen später an, als bei der vorhergehenden. Der Schlag fand statt, nachdem der
Kolben seinen Lauf beendigt hatte und sich wieder gegen die Treibachse bewegte. 3)
Die Stöße fangen an sehr bemerkbar zu werden. 4) Sie sind sehr stark.
Textabbildung Bd. 184, S. 98
Nr. der Versuche; Gewicht der per Sec. verbrauchten Wassermenge ΔQ;
Gefälle, bis zur Treibachse gemessen H'; Totales Gefälle H; Totale Arbeitsgröße
von ΔQH' ΔQH; Anzahl der Umdrehungen per Minute N; Geschwindigkeit
des Bremshebels per Sec. V = 0,2094395 N; Gewicht auf der Waagschale P;
Nutzeffect PV; Ergebniß des Wirkungsgrades; PV/ΔQH' PV/ΔQH';
Theoretisches Ergebniß des Wirkungsgrades; Volumen welches v. Kolben erzeugt
wird; Q' = 0,0000402124 N; Differenz von Q – Q'; Kolbengeschwindigkeit
per Sec. v = 0,008 N; Versuchsreihe; Dieselben Anordnungen wie bei der ersten
Reihe, mit Ausnahme des Hahnes, dessen Querschnitt gleich 4/5 von jenem der
Röhre war.; Kil.; Met.; Lit.; Dieselben Anordnungen wie bei der
ersten Reihe, mit Ausnahme des Hahnes, dessen Querschnittsöffnung nur 2/5 von
jener der Röhre betrug;
1) Bewegung sehr sanft. 2) Bewegung sanft. 3) Die Stöße und das
Geräusch begannen bemerkbar zu werden. 4) Sie vermehren sich. 5) Sie sind sehr
stark. 6) Bewegung sehr sanft. 7) Die Stöße und das Geräusch fiengen an bemerkbar zu
werden. 8) Sie vermehren sich bis zum Ende der Reihe, wo sie sehr stark sind.
Textabbildung Bd. 184, S. 99
Nr. der Versuche; Gewicht der per Sec. verbrauchten Wassermenge ΔQ;
Gefälle, bis zur Treibachse gemessen H'; Totales Gefälle H; Totale Arbeitsgröße
von ΔQH' ΔQH; Anzahl der Umdrehungen per Minute N; Geschwindigkeit
des Bremshebels per Sec. V = 0,2094395 N; Gewicht auf der Waagschale P;
Nutzeffect PV; Ergebniß des Wirkungsgrades;
PV/ΔQH' PV/ΔQH'; Theoretisches Ergebniß des Wirkungsgrades;
Volumen welches v. Kolben erzeugt wird. Q' = 0,0000402124 N; Differenz von Q
– Q'; Kolbengeschwindigkeit per Sec. v = 0,008 N; Versuchsreihe;
Dieselben Anordnungen wie bei der ersten Reihe, den Hahn ausgenommen, welcher
weder eine Verengung noch eine Erweiterung darbot; Met.; Lit.;
Die Zuleitung hat einen Durchmesser von 0,045 Met. und ist ohne Hahn; Die
übrigen Umstände waren dieselben wie bei der ersten Reihe
1) Bewegung sehr sanft. 2) Bewegung sanft. 3) Die Stöße und das
Geräusch fiengen an bemerkbar zu werden 4) Sie nahmen bemerklich zu. 5) Die Stöße
waren sehr stark. 6) Bewegung sehr sanft. 7) Bewegung sanft. 8) Ein wenig Geräusch
und Stöße.
Textabbildung Bd. 184, S. 100
Nr. der Versuche; Gewicht der per Sec. verbrauchten Wassermenge ΔQ;
Gefälle, bis zur Treibachse gemessen H'; Totales Gefälle H; Totale Arbeitsgröße
von ΔQH' ΔQH; Anzahl der Umdrehungen per Minute N; Geschwindigkeit
des Bremshebels per Sec. V = 0,2094395 N; Gewicht auf der Waagschale P;
Nutzeffect PV; Ergebniß des Wirkungsgrades; PV/ΔQH' PV/ΔQH';
Theoretisches Ergebniß des Wirkungsgrades; Volumen welches v. Kolben erzeugt
wird; Q' = 0,0000402124 N; Differenz von Q – Q'; Kolbengeschwindigkeit
per Sec. v = 0,008 N; Versuchsreihe; Dieselben Anordnungen wie für die fünfte
Reihe, ausgenommen daß das Schwungrad durch ein anderes vom Gewicht 22,30 Kil.
ersetzt worden war; Kil.; Met.; Lit.; Dieselben Anordnungen wie
für die 5. Reihe; Auf der mit der Ausflußröhre in Verbindung stehenden äußeren
Umhüllung hatte man aber zur Rechten und zur Linken kleine Hähne angebracht, die
man beide während dieser Versuchsreihe öffnete
1) Bewegung sanft. 2) Bewegung ziemlich sanft.; 3) Die Stöße
und das Geräusch sind bemerklich. 4) Sie nehmen zu, besonders das Eisengetöse. 5)
Viel Stöße und viel Lärm. 6) Bewegung sehr sanft. 7) Die Stöße und das Geräusch
beginnen bemerkbar zu seyn. 8) Sie nehmen bemerklich zu. 9) Stöße sehr bemerklich
und das Cisengetöse sehr stark.
Textabbildung Bd. 184, S. 101
Nr. der Versuche; Gewicht der per Sec. verbrauchten Wassermenge ΔQ;
Gefälle, bis zur Treibachse gemessen H'; Totales Gefälle H; Totale Arbeitsgröße
von ΔQH' ΔQH; Anzahl der Umdrehungen per Minute N; Geschwindigkeit
des Bremshebels per Sec. V = 0,2094395 N; Gewicht auf der Waagschale P;
Nutzeffect PV; Ergebniß des Wirkungsgrades; PV/ΔQH' PV/ΔQH';
Theoretisches Ergebniß des Wirkungsgrades; Volumen welches v. Kolben erzeugt
wird; Q' = 0,0000402124 N; Differenz von Q – Q'; Kolbengeschwindigkeit
per Sec. v = 0,008 N; Versuche, welche in den Wasserwerken der
Paulin-Straße zu Bordeaux angestellt wurden; Versuchsreihe; Die kleinen
Hähne auf der Umhüllung blieben während der ganzen Versuchsreihe geöffnet; Kil.;
Met.; Lit.;
1) Man konnte nicht mehr als 3,20 Kil. auf die Waagschale
legen, und selbst bei diesem Gewicht reichte der Druck kaum hin. 2) Der Gang ist gut
und regelmäßig. 3) Es gab nun Geräusch und Klappern. 4) Der Apparat auf dem Gestell
zitterte zu stark. als daß man hätte fortfahren können.
Textabbildung Bd. 184, S. 102
Nr. der Versuche; Gewicht der per
Sec. verbrauchten Wassermenge ΔQ; Gefälle, bis zur Treibachse gemessen
H'; Totales Gefälle H; Totale Arbeitsgröße von ΔQH' ΔQH; Anzahl
der Umdrehungen per Minute N; Geschwindigkeit des Bremshebels per Sec. V =
0,2094395 N; Gewicht auf der Waagschale P; Nutzeffect PV; Ergebniß des
Wirkungsgrades; PV/ΔQH' PV/ΔQH'; Theoretisches Ergebniß des
Wirkungsgrades; Volumen welches v. Kolben erzeugt wird; Q' = 0,0000402124 N;
Differenz von Q – Q'; Kolbengeschwindigkeit per Sec. v = 0,008 N;
Versuche zu Arcachon; Versuchsreihe; Kil.; Met.; Lit.
1) Man hat die Versuche begonnen mit einem Gewicht von 5 Kil.
Die kleinen Hähne waren offen, der Bremshebel war leicht zu reguliren, die Bewegung
sanft 2) Weniger sanft 3) Das Excentric heiß 4) Ein wenig sanfter. 5) Sanft bis an's
Ende.
(Der Schluß folgt im nächsten Heft.)
Tafeln