| Titel: | Ueber thermoelektrische Pyrometrie; von C. Schinz. |
| Autor: | C. Schinz |
| Fundstelle: | Band 177, Jahrgang 1865, Nr. XIX., S. 85 |
| Download: | XML |
XIX.
Ueber thermoelektrische Pyrometrie; von C. Schinz.
Mit Abbildungen auf Tab.
II.
Schinz, über thermoelektrische Pyrometrie.
Im Februar 1862 beschrieb ich in diesem Journal (Bd. CLXIII S. 321) einen
pyrometrischen Apparat, welcher auf dem Principe der Leitungsfähigkeit der Ofenwände
für die Wärme beruht. Leider hat diese Methode sich zur Bestimmung höherer
Temperaturen nicht bewährt; meine im Laboratorium bis 500° und 600° C.
reichenden Versuche hatten übereinstimmende Resultate gegeben, aber bei
Temperaturen, welche zwei- bis dreimal die eben genannten überschreiten,
ändert sich die Leitungsfähigkeit des feuerfesten Thones so merklich, daß damit
keine brauchbaren Resultate erhalten werden können.
Schon zu der Zeit, wo ich mich mit diesen Versuchen beschäftigte, hatte ich zwischen
dem thermoelektrischen Pyrometer von Pouillet und dem
beschriebenen Apparat zu wählen; die so leicht stattfindende Veränderung des
Flintenrohres von Pouillet einerseits und andererseits
der unvollkommene und wenig empfindliche Meßapparat, dessen er sich zur Bestimmung
der Stromintensität bediente, bestimmten mich aber, dem Principe der
Wärmeleitungsfähigkeit der Ofenwände den Vorzug zu geben.
Ein dritter Vorschlag, bestehend in der Anwendung eines thermoelektrischen Elementes
von Platin-Palladium, welches bei hohen Temperaturen weniger leicht als Eisen
der Veränderung unterworfen ist, beschäftigte mich damals ebenfalls, allein der
Mangel an einem hinlänglich empfindlichen und zuverlässigen Rheometer zur Bestimmung
der Stromintensitäten bestimmte mich, auch diesem Vorschlage keine Folge zu
geben.
Nachdem sich nun gezeigt hatte, daß bei hohen Temperaturen die Leitungsfähigkeit
nicht als pyrometrisches Mittel dienen kann, so begrüßte ich freudig ein Jahr später
(Mai 1863) die in den Annales de Chimie et de Physique,
3e série p. 49 von Ed. Becquerel mitgetheilte Arbeit über ein Pyrometer, das eben auf der
Stromintensität des thermoelektrischen Elementes Platin-Palladium beruht.
Der von Ed. Becquerel beschriebene Apparat war indessen zu
sehr ein Cabinetsstück, als daß derselbe sich sofort hätte in die Praxis übertragen
lassen; doch enthielt er scheinbar alle Elemente, um ihn nach einigen Modificationen
auch in den Werkstätten der pyrotechnischen Industrie verwendbar zu machen.
Sowohl das dringend gefühlte Bedürfniß, für die Praxis ein leicht zu manipulirendes,
zuverlässiges und auf gewöhnliche Thermometergrade reducirbares Pyrometer zu
besitzen, als die Aussicht, vermittelst der von Ed. Becquerel mitgetheilten Resultate dieses Problem zur Lösung zu bringen,
bestimmten mich dann, sogleich diese Arbeit zu unternehmen.
Indem ich aber dabei auf die Zuverlässigkeit und Genauigkeit der Becquerel'schen Arbeit zählte, hatte ich mich bitter
getäuscht; ich hatte Schritt für Schritt Unzuverlässigkeiten und Fehlerquellen in
derselben zu constatiren, diese nach und nach zu beseitigen und alle Apparate
wiederholt neu zu construiren, so daß die nun vollendete Arbeit zwei Jahre
Zeitaufwand und sehr bedeutende Kosten veranlaßt hat.
Als Rheometer hat sich Becquerel eines sogenannten
Magnetometers bedient, welches in einem stark magnetischen Stabe besteht, der an
einem Coconfaden aufgehängt ist; über dem Magnetstabe befindet sich ein Spiegel, auf
dem man auf einige Meter Entfernung die Ablenkung vermittelst eines Fernrohres und
eines Tangenten-Maaßstabes abliest; der Magnetstab selbst ist in einem mit
Kupferdrähten umwundenen Rahmen eingesenkt. Das Rheometer soll nach Becquerel nur auf 3 bis 4° abweichen und der Rest
der Stromintensität durch eingeschaltete Widerstands-Drahtspulen gemessen
werden.
Die Empfindlichkeit dieses Magnetometers ist wahrhaft staunenerregend, so daß ich bei
den ersten Versuchen glaubte nun wirklich einen solchen Grad der Vollkommenheit
erreicht zu haben, daß ich trotz aller Complicirtheit desselben es für
gerechtfertigt gehalten hätte, dasselbe in die Praxis überzuführen.
Bei meinen Versuchen mit diesem Magnetometer kam ich endlich auch dazu, das
Platin-Palladium-Element steigend höheren Temperaturen auszusetzen.
Für Temperaturen die etwa bis 400° giengen, fand ich zwar die erzeugten
Stromintensitäten etwas weniger schnell mit der Temperatur wachsend als Becquerel angibt; allein solche Differenzen werden und
müssen sich immer ergeben, wenn die als Elemente angewandten Metalle nicht identisch
sind; wenigstens stiegen die Intensitäten ziemlich regelmäßig rascher als die
denselben entsprechenden Temperaturen. Als ich aber circa 448°, die Temperatur des schmelzenden Antimons, erreicht
hatte, blieb mein Strom-Meßapparat völlig unbeweglich, ja er hatte sogar die Tendenz
rückwärts zu gehen, so daß also die beiden Drähte Platin-Palladium sich
gerade so verhielten wie viele andere Metalle, welche bei gewissen Temperaturen
stillstehen und dann bei Glühtemperatur einen negativen Strom erzeugen, während er
bei niedrigen Temperaturen positiv war. Obgleich ich den Versuch mehreremale
wiederholte und selbst verschiedene Platindrähte mit dem Palladiumdrahte verband, so
erhielt ich doch immer dasselbe Resultat. Ich wandte mich nun. brieflich an die
Lieferanten der Platin- und Palladiumdrähte, die HHrn. Desmontis und Quenessen in Paris, theilte
denselben die erhaltenen Resultate mit, forderte sie auf, mit Hrn. Becquerel zu conferiren und mir solche Drähte zu
verschaffen wie die, von denen Becquerel angibt, daß sie
ihm von 0° bis 1150° Temperatur ziemlich gleichförmig wachsende
Intensitäten geliefert haben; mein erster Brief wurde höflich beantwortet, aber das
gegebene Versprechen, die Drähte zu liefern, wurde nicht gehalten und spätere
Briefe, in denen ich Erfüllung des Versprochenen verlangte, blieben ohne
Erwiederung. Der Palladiumdraht, welchen ich besitze, hat übrigens alle chemischen
und physikalischen Eigenschaften des Palladiums, so daß kaum zu begreifen ist, wie
eine solche absolute Verschiedenheit der Resultate erhalten werden konnte.
Es blieb mir also nichts anderes übrig, als zu dem Elemente Platin-Eisen,
welches Pouillet angewandt hatte, zurückzugreifen; statt
aber einen Flintenlauf zu wählen, nahm ich einen runden Eisenstab von 7 Millimeter
Durchmesser und ließ mir gleich einen großen Vorrath solcher Stäbe von einer und
derselben Drahtrolle zurichten, damit ich dieselben auswechseln konnte, wenn einer
sich veränderte. Diese Stäbe sind an beiden Enden rechtwinkelig durchbohrt, so daß
am einen Ende der Platindraht, am anderen ein Eisendraht durch einen eisernen Keil
solid befestigt werden können. Das so zugerichtete Element schiebe ich dann in eine
15 Millimeter weite Röhre von Eisen oder auch von feuerfestem Thone und umgebe darin
das Element mit feinem Quarzsand. Statt der 7 Millim. dicken Eisenstäbe 2 Millim.
dicken Draht zu nehmen, geht nicht, indem solcher Draht trotz der Umhüllung mit Sand
schon in einer Operation verbrennt, während 7 Millim. dicke Stäbe kaum angegriffen
werden.
Bei fortgesetzten Versuchen mit dem Platin-Eisen-Element und dem
Magnetometer ergab sich nun, daß letzteres trotz seiner merkwürdig gesteigerten
Empfindlichkeit unanwendbar ist, denn gerade diese Empfindlichkeit hat auch gezeigt,
daß alle Magnetometer, d.h. alle Strommesser in welchen die magnetische Kraft durch
den elektrischen Strom zu überwinden ist, unbrauchbar sind, weil die Declination der
Magnetnadel nicht – wie man vermuthen möchte, wenn man in den Lehrbüchern der
Physik von den täglichen Schwankungen liest – eine allmähliche ist, sondern
oft innerhalb einer Stunde 15 Minuten beträgt, so daß nach sehr kurzer Zeit die
Nadel nach Aufhebung des Stromes eben so wenig auf 0° zurückgeht, als dieß
mit einer astatischen Nadel der Fall ist.
Es besteht nur der Unterschied, daß das Magnetometer selbst diese Declination von 15
Minuten angibt, während sie beim gewöhnlichen Galvanometer der Beobachtung entgeht.
100 Stromintensitäten entsprachen am Magnetometer ungefähr 2° 51' = 171
Minuten; wenn daher wegen der Declination die Beobachtung auf 15 Minuten unsicher
wird, so entspricht das 8 bis 9 Intensitäten, und da diese Stromstärke von 31,5 oder
108,5 statt 100 Intensitäten auf den Rheostatendraht wirkt, so multiplicirt sich
also auch hier der Beobachtungsfehler mit der Länge des abgewickelten Drahtstückes,
und eine Uebereinstimmung der Resultate ist weder zu erwarten noch erhalten worden.
Wie eine so bedeutende Fehlerquelle Hrn. Becquerel
entgehen konnte, ist kaum begreiflich.
Es mußte also das Magnetometer abgedankt werden; ehe ich aber von dem Meßapparate
spreche, der dann endgültig dieses ersetzt hat, will ich noch der complicirten
Rechnungen erwähnen, welche der magnetometrische Meßapparat erforderte.
Die Leitungsfähigkeit sowohl der Leitungsdrähte vom thermoelektrischen Elemente in
das Rheometer, als die der Windungen in diesem selbst, wechselt mit der Temperatur
derselben; diese Drähte absorbiren also je nach der Temperatur die sie haben, mehr
oder weniger von der Stromintensität. Um nun diesen Einfluß, welcher eine nicht ganz
unbedeutende Fehlerquelle ist, zu umgehen, bestimmte Becquerel vor jedem Versuche die Intensität des Stromes, indem er das
thermoelektrische Element in einen Strom von Wasserdämpfen brachte und bezeichnete
die so erhaltene Stromstärke mit 100 Intensitäten, so daß er die darauf folgenden
Versuche immer auf diese Urintensität 100 bezog. Vor jedem Experimente diese
Vorbestimmung machen zu müssen, ist nicht nur sehr zeitraubend und umständlich,
sondern es verbirgt dieselbe nicht einmal übereinstimmende Resultate; denn in einem
Raum, worin solche Versuche gemacht werden, kann die Temperatur nicht constant
bleiben und somit auch nicht die Leitungsfähigkeit der Drähte; obgleich ich meinen
Ofen in einem abgesonderten Zimmer habe, so steigt doch selbst in dem Zimmer, worin
sich das Rheometer befindet, die Temperatur binnen wenigen Stunden um mehrere
Grade.
Es ist also viel sicherer, diesen Einfluß der Temperatur durch Rechnung einer
Correction zu unterwerfen, indem man bei jedem Versuche die Temperatur der Luft
bestimmt.
Was nun die Sache einigermaßen complicirt macht, ist, daß für jede
Intensitäts-Bestimmung zuerst die normale Stromstärke bestimmt werden muß.
Wäre z.B. bei 13,5° Temperatur die normale Stromstärke von 100 Intensitäten
am Tangenten-Maaßstabe = 180 Millimeter, die Temperatur der Luft aber bei
Beginn des Versuches = 21°, so sind jene 180 durch 1 + xt zu dividiren, wo x
= dem Widerstands-Coefsicienten für 1° Temperatur ist.
21 – 13,5 = 7,5 = t, daher
180/(1 + 0,004091 . 7,5) = 173,53.
Eine andere Fehlerquelle, welche Becquerel ganz außer Acht
gelassen hat, bildet die wechselnde Intensität des Erdmagnetismus, welche die
Magnetnadel in den Meridian zurückzutreiben strebt. Auch diese Variationen sind viel
häufiger als man glaubt, wovon ich mich durch einige Tage fortgesetzte Versuche
überzeugt habe; wenn die Schwingungsdauer des Magnetstabes nur 2,7 Secunden war,
wurde sie zuweilen innerhalb 24 Stunden = 3,0.
Nehmen wir nun die normale Schwingungsdauer = 3 Secunden = z an, so ist, die durch den Strom überwundene
magnetische Kraft = 1 gesetzt, diese Kraft (z₁/z = 2,7²/3² = 0,81)
nur noch 0,81, wenn die Schwingungsdauer sich auf 2,7 Secunden vermindert hat, und
wir haben daher die normale Tangente 180 für die Stromstärke 100, welche durch
Temperaturerhöhung auf 173,53 erniedrigt wurde, durch 0,81 zu dividiren, wodurch
diese Tangente 173,53/0,81 = 214,23 Millim. wird.
Somit haben jeder Bestimmung mit dem Magnetometer die Correctionen für Temperatur und
für magnetische Intensität vorauszugehen, und ist dann der Index am
Tangenten-Maaßstabe statt auf die normalen 180 Millimeter für 13,5°
Temperatur und 3 Secunden Schwingungsdauer, auf die corrigirte Tangente 214,23
Millim. zu stellen.
Nun erfährt aber auch der Rheostatendraht durch die Temperatur eine Modification
seines Widerstandswerthes, folglich muß auch dieser corrigirt werden. Wenn daher der
Werth einer Rheostatenspirale von Neusilber bei der Normaltemperatur = 38
Intensitäten ist, so wird er bei der Temperatur 21° = 38/(1 + x₁t), wo x₁ = dem
Leitungscoefficienten für 1°, den ich zu 0,0003768 bestimmt habe.
Hätten wir daher beispielsweise 3,79 Spiralen abgewickelt, um den Index am
Tangenten-Maaßstabe auf 214,23 zu erhalten, welche 100 Intensitäten anzeigen,
so wären diesen 100 zuzuzählen (3,79 . 38)/(1 + 0,0003768 (21 – 13,5)) =
143,64. Auch diese Fehlerquelle hat Becquerel außer Acht
gelassen.
Nachdem ich nun auf diese Weise eine Menge negativer Erfahrungen gemacht hatte und
dabei veranlaßt war, mir über alle Einflüsse und Bedingungen genaue Rechenschaft zu
geben, kam ich endlich auf den Gedanken, statt dem thermoelektrischen Strome die
variable Kraft des Magnetismus entgegenzusetzen, denselben durch die Torsion eines Metallfadens zu ersetzen, wodurch es
zugleich möglich wird, des Rheostaten gänzlich zu entbehren und dadurch den ganzen
Apparat sehr zu vereinfachen. Dieses unbestreitbar richtige Princip ließ nur noch
das Problem übrig, dem Apparate die größtmögliche Empfindlichkeit zu geben; dieses
erreichte ich, indem ich als Torsionsfaden einen Silberdraht von 1/10 Millim.
Durchmesser wählte, demselben 900 Millimeter Länge gab und daran eine 300 Millim.
lange vollkommen asiatische Nadel in einem großen Rheometerrahmen mit dicken
Kupferdrähten aufhieng; indem ich ferner dem Theilkreise zur Messung der Torsion 490
Millim. Durchmesser gab, so daß die auf demselben befindlichen 720 Theilstriche
etwas mehr als 2 Millimeter von einander entfernt sind, was auch diese Theile noch
auf halbe Theile abzuschätzen gestattet.
Die Wahl der Dicke des Torsionsdrahtes ist von großer Wichtigkeit, weil hauptsächlich
von dieser die Empfindlichkeit des Instrumentes abhängt, denn die von dem Strome zu
überwindende Torsionskraft ist umgekehrt proportional dem Querschnitte.
Je dünner und länger daher der Draht ist, desto größer wird der Torsionswinkel für
eine und dieselbe Stromstärke ausfallen. Indessen findet sich da bald eine Grenze,
theils in der leichten Zerbrechlichkeit sehr dünner Drähte, theils in dem Umstande,
daß bei zu großer Empfindlichkeit es auch viel schwieriger würde, die asiatische
Nadel immer genau auf Null zu bringen.
Das praktisch richtigste Verhältniß ist, wenn der Faden für die Stromintensität,
welche durch 1000° Temperatur hervorgebracht wird, sich etwa um 360°
dreht, so daß bei den höchsten Temperaturen nicht über 1 1/2 Umdrehungen
erforderlich sind. Allerdings wird dadurch bei niedrigen Temperaturen die Torsion
für einen Grad Temperatur sehr klein, bei höheren
Temperaturen aber immerhin 1 bis 2 Grade, was, da unser Kreis 720 Theile umfaßt, 2
bis 4 Theile oder Intensitäten ausmacht.
Die Torsionskraft des Fadens, welche dem thermoelektrischen Strome entgegengesetzt
wird, kann durch mancherlei Umstände modificirt werden, z.B. durch Lähmung nach
längerem Gebrauche, durch Veränderung der angehängten Gewichte (astat. Nadel), durch
Temperatur, besonders durch Verkürzung oder Verlängerung des Fadens, und ein und
derselbe Draht, welcher durch dasselbe Zieheisen gezogen ist, zeigt bei
verschiedenen Stücken desselben etwas wechselnde Torsionskraft. Wenn daher wegen des
Einflusses dieser Umstände es nicht möglich ist, immer genau dieselbe Kraft dem
Strome entgegenzusetzen, so geht daraus die Nothwendigkeit hervor, diese genau zu
prüfen und für Abweichungen von der normalen Kraft eine Correction eintreten zu
lassen.
Um diese Prüfung vorzunehmen und darnach die Correction, kann man einfach die am
Silberfaden hängende astatische Nadel in Schwingung versetzen, indem man durch ein
Stück Eisen die Nadel um 10° bis 20° ablenkt. Dadurch wird die Torsion
wirksam und dieselbe nöthigt die Nadel zurückzukehren; sie kehrt aber nicht bloß in
ihre frühere Lage auf den Nullpunkt zurück, sondern erlangt, wie das Pendel, eine
gewisse Geschwindigkeit, welche sie fast eben so weit über den Nullpunkt
zurücktreibt, als sie vorher zum Abweichen gebracht wurde. Es entstehen
Schwingungen, deren Dauer dem Quadrate der Torsionskraft proportional ist. Wenn also
im einen Falle die Dauer einer Schwingung 25 Secunden, im anderen Falle 26 Secunden
wäre, so würde die Torsionskraft, im ersten Falle gleich 1 gesetzt, im zweiten Falle
= 25²/26² = 0,92458 seyn.
Ein und derselbe thermoelektrische Strom wird daher im zweiten Falle eine 0,92458 Mal
größere Wirkung Hervorbringen und um daher die Correction zu machen, genügt es die
beobachtete Torsion mit 25²/26² zu multipliciren.
Natürlich soll zu den Beobachtungen die Torsion immer so gleich als möglich seyn; da
aber kleine Abweichungen unvermeidlich sind, so ist eine häufige Messung der
Torsionskraft durchaus nothwendig.
Zu dieser Messung sind einige Vorsichtsmaßregeln nothwendig. Der Betrag der
Schwingungen soll nur klein seyn, so daß die Nadel keinen großen Weg zu machen hat
und sich daher langsam bewegt. Nie soll eine Schwingung allein gemessen werden,
sondern deren wenigstens vier. Man nimmt eine gute Secundenuhr, setzt den
Secundenzeiger in dem Momente in Bewegung, wo die Nadel auf dem Nullpunkte
angekommen ist und arretirt dann wenn diese zum fünften Male den Nullpunkt berührt; die Zahl der
verflossenen Secunden, durch 4 dividirt, gibt die Dauer einer Schwingung.
Ein frisch eingehängter Silberfaden gibt stets weniger Schwingungen, als dann, wenn
die Nadel schon mehrere Tage daran gehangen hat, wenn auch diese nur ein sehr
geringes Gewicht hat; man muß daher das Gewicht der astatischen Nadel nicht größer
als nöthig machen, immerhin aber der Art, daß der Faden vollkommen geradlinig
herabhängt.
Es bleibt noch zu bemerken, daß zwei Torsions-Rheometer, auch wenn sie genau
dieselben Schwingungszeiten hätten, dennoch möglicherweise nicht dieselbe
Torsionskraft haben können, weil nicht die Torsionskraft allein wirkt, sondern auch
noch die Masse der astatischen Nadel; um daher die Stromstärke eines
thermoelektrischen Elementes zu bestimmen, sollte man immer dasselbe
Torsions-Rheometer anwenden, welches nachher zu den pyrometrischen Versuchen
benutzt wird.
Die Corrections-Coefficienten für Schwingungszeiten von 24 bis 30 Secunden,
für die Normalzeit 25 Secunden, sind in der unten folgenden Tabelle B angegeben.
Für Platin-Eisen-Elemente, mit denen man hohe Temperaturen messen will,
sollte die Schwingungszeit so nahe als möglich 25 Secunden betragen.
Die Einwirkung der Temperatur auf die Leitungs- und Rheometerdrähte ist
natürlich die gleiche, welches auch das Meßinstrument für die Intensität der Ströme
sey, und es muß daher auch für diese die Correction vorgenommen werden. In der unten
folgenden Tabelle A finden sich die
Corrections-Coefficienten für die Lufttemperaturen von 0° bis
35°.
Dagegen fällt nun glücklicher Weise sowohl die Correction als überhaupt die Anwendung
und Beobachtung des Rheostaten weg, indem eine volle
Torsion des Silberfadens genügt, um selbst diejenigen Stromintensitäten zu messen,
welche der Temperatur 1000° entsprechen.
Es versteht sich, daß die astatische Nadel stets auf dem Nullpunkte der Gradbogen zu
stehen hat, zwischen welchen dieselbe sich zu bewegen strebt, und daß nur der Hebel
an der Rotationsachse auf dem Theilkreise zu bewegen ist.
Da nun die Gradbogen, zwischen welchen sich die asiatische Nadel bewegt, 150
Millimeter Radius haben, so ist das Einstehen auf dem wirklichen Nullpunkte leicht
zu beobachten, und sollte selbst darin ein sehr kleiner Beobachtungsfehler gemacht
werden, so ist derselbe ganz ohne Einfluß, insofern er nicht mehr durch einen
Rheostatendraht multiplicirt wird.
Der Rheometerrahmen ist von dickem Kupfer angefertigt, so daß, wenn der Strom durch
die Windungen geht, ein Gegenstrom entsteht, der die Schwingungen der Nadel sehr
verkürzt. In der That weicht die Nadel nicht mehr als 1 bis 2 Grade ab, wenn man den
Torsionsachsen-Hebel allmählich mit der steigenden Stromintensität vorwärts
schiebt und die Nadel kommt ohne zu oscilliren mit der steigenden Stromintensität
allmählich wieder auf Null; eine Eigenschaft, welche die früher versuchten
Rheometersysteme durchaus nicht hatten.
Auch geht die Nadel nach Abstellung des Stromes stets genau auf Null zurück, wenn man
den Torsionshebel ebenfalls auf Null einstellt.
Dieses Torsions-Rheometer hat endlich einen nicht unbedeutenden Vorzug vor den
von mir aufgegebenen Strommessern darin, daß man jeden der 720 Grade des
Theilkreises für die Torsion als eine Stromintensität
nehmen kann, ohne daß man nöthig hat durch Rechnung dieselbe auf eine bestimmte
Einheit zurückzuführen, wie dieß bei den anderen Strom-Meßapparaten der Fall
war.
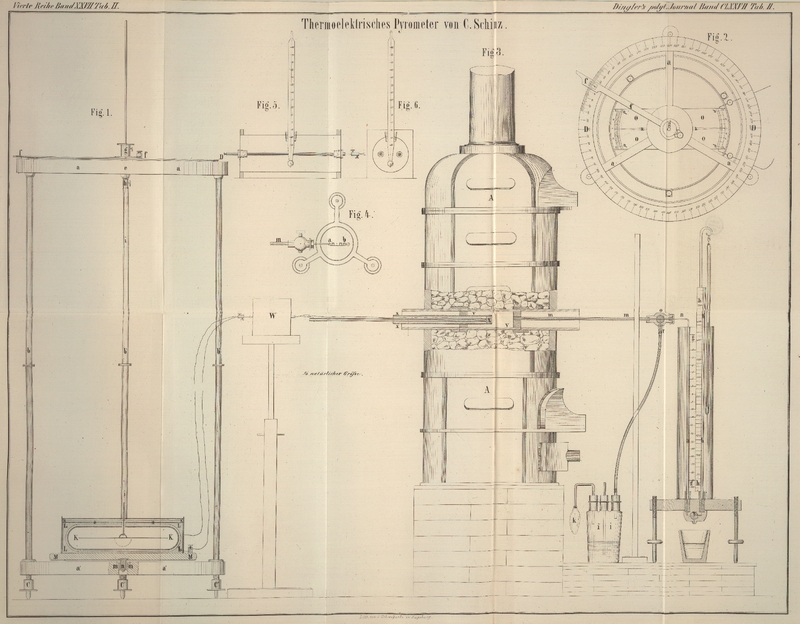
Dieses Torsions-Rheometer ist in den Figuren 1 und 2 abgebildet.
Das Gestell desselben besteht aus zwei Holzkreuzen a,
a', welche durch drei hohle Messingsäulen b, b',
b'' mit einander verbunden sind; die Füße dieser Säulen sind mit
Stellschrauben C, C', C'' versehen, um das Ganze in
vollkommen verticale Richtung zu bringen.
Auf dem oberen Kreuze a ruht der in 720 Theile getheilte
Theilkreis D, D, welcher 49 Centimeter äußeren
Durchmesser hat und in dessen Mitte ein hohler Zapfen e
(Fig. 1)
sich dreht, auf dem der Zeiger f befestigt ist. Ueber
diesem Zapfen e ist ein Messingstück g, welches ebenfalls hohl ist und das die durch den
Zapfen e durchgehende Zange h mittelst einer Schraube festhält; durch eine andere Schraube wird das
Stück g mit dem Zeiger f
befestigt, so daß die Zange h mit dem Zeiger f sich dreht.
Die Zange h nimmt den Torsionsdraht i auf; derselbe hat 90 bis 100 Centimeter Länge und
einen sehr kleinen Durchmesser. Da die Zange h eine
gewisse Länge hat, so ist es möglich dem Drahte i, i
eine größere oder kleinere Länge zu geben.
Unten an dem Draht i, i hängt die astatische Nadel k, k von trapezoidaler Form, aus Uhrfederstahl
gefertigt, 30 und 20 Centimeter lang. An der unteren Nadel K,
K hängt ein kleines Messinggefäß, um durch Anlegen von Gewichten den Draht
i, i mehr oder weniger belasten zu können.
Der Rheometerrahmen L, L ist von starkem Kupfer
gefertigt; der auf demselben aufgewundene Draht hat 2 Millimeter Stärke und eine
Gesammtlänge von 18,2 Meter. Da der Rahmen aus Kupfer besteht, so ist besondere
Sorgfalt auf die Isolirung der Kupferdrähte zu verwenden.
Dieser Rahmen ist auf der Holzscheibe M, M befestigt, mit
einer messingenen kreisförmigen Zarge umgeben und diese durch eine runde Glasplatte
mit kleiner Oeffnung in der Mitte, durch welche der Draht i,
i geht, gedeckt. Die Scheibe M, M trägt den
conischen Zapfen n, der sich in einem messingenen Futter
m, welches im Holzkreuze a' befestigt ist, frei dreht.
Ueber dem Rheometerrahmen ist das Messingblech o, o
angebracht, welches an beiden Enden mit den Gradbogen p,
p (Fig.
2) versehen ist, auf denen die obere Nadel k,
k schwebt. Da die Nadel immer auf dem Nullpunkte der beiden Bogen p, p erhalten werden soll, so brauchen diese nur einen
kleinen Umfang zu haben.
Das Problem eines thermoelektrischen Pyrometers ist aber seiner Lösung noch sehr
ferne, nachdem die Mittel gefunden sind, die erzeugten Stromintensitäten mit
Genauigkeit zu messen; ja es ist sogar das Auffinden dieser Mittel unmöglich, ohne
gleichzeitig die Mittel zu besitzen, diese Stromintensitäten mit der Temperatur zu
vergleichen, welche jene hervorbringt, und dieser zweite Theil der Aufgabe bietet
kaum weniger Schwierigkeiten dar, als der erste.
Selbst die Bestimmung niedriger Temperaturen innerhalb der Grenzen des
Quecksilberthermometers erheischt zahlreiche Vorsichtsmaßregeln, um sicher zu seyn,
daß das thermoelektrische Paar wirklich die Temperatur angenommen hat, welche das
controlirende Thermometer anzeigt, und diese Schwierigkeit wird noch bedeutend
dadurch erhöht, daß wirklich genaue Thermometer kaum existiren.
Da indessen hier von Pyrometern die Rede ist, so übergehen wir die Bestimmung
niedriger Temperaturen und betrachten nur die Mittel, höhere Temperaturgrade zu
bestimmen.
Solcher Mittel gibt es eigentlich nur eines, nämlich die
Ausdehnung der Gase durch Temperaturerhöhung; nur kann dasselbe verschieden
angewandt werden.
Anfangs glaubte ich der Regnault'schen MethodePolytechn. Journal Bd. CLXII S. 361. den Vorzug geben zu müssen. Dieselbe besteht darin, daß man eine Röhre von
Porzellan oder Eisen an beiden Enden mit capillaren Ausmündungen versieht, welche
mit Zweiweghahnen endigen. Man umgibt für einen ersten Versuch die Röhre mit Eis und
läßt von der einen Seite wohl gereinigtes getrocknetes Wasserstoffgas einströmen,
das die Luft in der Röhre verdrängen soll, indem man die in der Röhre enthaltene
Luft und den überschüssigen Wasserstoff entweichen läßt. Ist die Röhre mit Wasserstoff gefüllt, so
wird der Einströmungshahn so gestellt, daß nun trockene atmosphärische Luft in die
Röhre dringt; der Ausflußhahn wird so gestellt, daß die nun aus der Röhre dringenden
Gase in eine rothglühend erhaltene, mit getrocknetem Kupferoxyd gefüllte Röhre
ziehen; das Kupferoxyd verbrennt dann allen Wasserstoff und bildet Wasser, das in
einer vorgelegten Chlorcalciumröhre aufgefangen und nach beendeter Operation gewogen
wird.
Dadurch erfährt man, welches die Capacität der Röhre ist.
Hätten wir z.B. 0,512 Gramme Wasser erhalten, so entsprechen diese 0,056888 ... Grm.
Wasserstoff, und da 1000 Kubikcentimeter Wasserstoff bei 0° und 760 Millim.
Barometerstand = 0,08939 Grm. wiegen, so folgt daraus, daß die Capacität der Röhre =
636,32 Kubikcentimeter ist.
Soll nun eine Temperatur bestimmt werden, so wird dieselbe Operation wiederholt, mit
dem Unterschiede, daß jetzt die Röhre in den Raum gebracht wird, dessen Temperatur
man messen will. Die Einführung von Wasserstoff wird erst dann unterbrochen und
durch Einführung von Luft ersetzt, wenn die Röhre diejenige Temperatur erlangt hat,
welche man messen will.
Hätten wir nun bei dieser Bestimmung 0,256 Grm. Wasser erhalten = 0,028444 Grm.
Wasserstoff = 318,21 Kubikcentimeter, so wäre die Temperatur der Röhre eine solche
gewesen, die den Wasserstoff in der Röhre gerade auf das Doppelte ausgedehnt hätte,
und wäre folglich zwischen 272° und 273° gelegen, denn 636,32 ×
2 = 1272,64
und
636,32
(1 + a 272) = 1270,90
636,32
(1 + a 273) = 1273,20.
Nichts kann verführerischer erscheinen, als diese Methode der
Temperatur-Bestimmung, da das erhaltene Wasser neunmal mehr wiegt als der
Wasserstoff, welchen man bestimmen will. Leider bietet aber die praktische
Ausführung dieser Methode solche Schwierigkeiten dar, daß ich nach wenigen Versuchen
mich veranlaßt sah dieselbe gänzlich aufzugeben. Es fehlt nämlich an einem
Kriterium, welches uns sagt, wann die Röhre wirklich durchaus mit Wasserstoff
gefüllt ist und wann dieselbe wieder ganz von demselben entleert ist.
Besonders ist dieß schwierig, wenn die Röhre in Eis getaucht ist, und es ist
überhaupt nicht abzusehen, ob bei der Temperatur von 0° je der Inhalt der
Röhre sich mit Wasserstoff fülle oder vollständig entleere. Als ich im Verlaufe von
zwei Stunden wohl 18 Liter Wasserstoffgas durch die Röhre bei 0° geführt
hatte (bei einer Röhrencapacität von nur 0,242 Liter), erhielt ich durch Verbrennung
bloß etwa 1/3 so viel Wasser als ich hätte erhalten sollen. Ich glaube nicht, daß ohne
Hülfe einer Luftpumpe, vermittelst welcher die Röhre wohl 30 Mal entleert und mit
Wasserstoff wieder gefüllt würde, es dahin zu bringen sey, die Röhre wirklich
vollkommen mit reinem Wasserstoff zu füllen, und zur Verdrängung des Wasserstoffes
bei 0° bleibt uns nicht einmal das Hülfsmittel der Luftpumpe.
Diese Bestimmung des Volumens der Röhre ist, bei 0° wenigstens, gewiß
unmöglich richtig ausführbar. Ist hingegen die Röhre rothglühend, so kann es keine
große Schwierigkeit bieten, dieselbe mit Wasserstoff zu füllen, da alsdann auch die
kleinste Luftmenge schnell vom Wasserstoff verbrannt wird; aber auch dann fehlt es
an einem Kriterium, durch welches man erfährt, wann aller Wasserdampf und aller
Stickstoff wirklich evacuirt sind.
Dieses Alles berechtigt zu dem Schlusse, daß diese Methode zu viele Unsicherheit
bietet, um darauf genaue und richtige Temperatur-Bestimmungen gründen zu
können.
Andere Methoden, durch Ausdehnung der Luft die Temperatur zu bestimmen, beruhen auf
dem Messen des Volumens der ausgedehnten Luft.
Denken wir uns irgend ein Gefäß, welches mit einem Gas-Entwickelungsrohre
versehen ist und auf der anderen Seite eine Quecksilberwanne mit Meßapparat, in
welchem das aus dem Gefäße verdrängte Gasvolumen gesammelt wird. Bringen wir nun das
Gefäß in den Raum, dessen Temperatur wir messen wollen, so wird das in demselben
enthaltene Gas sich ausdehnen und in die Meßröhre über der Quecksilberwanne
entweichen.
Wäre beispielsweise die Capacität des Gefäßes bei 0° gerade aus 100
Kubikcentimeter = V und wir tauchen dasselbe in einen
Raum ein, der 500° Temperatur hat, so wird der Inhalt von V = 100 zu V' = V (1 + at) = 100 (1 + 0,003665 . 500) = 283,25 Kubikcentimeter;
da nun aber das Gefäß nur 100 Kubikcentimeter enthalten kann, so werden 283,25
– 100 = 183,25 Kubikcentimeter in die Meßröhre verdrängt werden; da aber
diese nicht 500° Temperatur hat, sondern eine viel niedrigere, so wird das
Volumen viel kleiner als 183,25 K. C.
Wenn wir aber die Temperatur des Gases in der Meßröhre genau kennen, so können wir
nach den gewöhnlichen Methoden dessen Volumen bei 0° und 760 Millim.
Barometerstand bestimmen.
Ist nun die Temperatur des Gefäßes wirklich 500°, so wird das verdrängte Volumen bei 0°
= 183,25/(1 + a 500) = 64,695 K. C. seyn; und da 100
– 64,695 = 35,305 K. C. = dem Inhalte des Gefäßes bei 500° ist, so muß
35,305 × (1 + a 500) wieder 100 Kub. Centim.
geben. Dieß ist im Allgemeinen eine der Methoden, nach welchen wir durch die
Ausdehnung der Luft volumetrisch die Temperatur bestimmen können.
Eine zweite Methode besteht darin, daß man das im Gefäße enthaltene Gas so weit
comprimirt, daß es sein Volumen behält und dann die wirksame Temperatur aus der
angewandten Pressung bestimmt.
Das Volumen des Gases im Gefäße sey wieder bei 760 Millim. Barometerstand und
0° Temperatur = 100 K. C.; es werde nun das Gefäß abermals in einen Raum
eingetaucht, dessen Temperatur 500° ist, so wird das Volumen von 100 K. C.
sich auf 100 . (1 + a 500) = 283,25 auszudehnen streben;
verbinden wir aber das Gefäß mit einem Manometer, welches hinreichenden Druck
auszuüben im Stande ist, um das Volumen auf 100 K. C. zu erhalten, so wird dieser
Druck V : V' = p : p' = 100 : 283,25 = 760 : 2152,7 und ist dieser Druck,
statt berechnet, beobachtet, so können wir aus demselben auf die unbekannte
Temperatur schließen.
Um nun diese beiden Methoden mit einander zu vergleichen und deren Werth prüfen zu
können, wollen wir die Werthe zusammenstellen, welche dieselben für die Temperaturen
0° bis 1300°, um je 100° steigend, ergeben.
Die Columne
A
gibt die Temperaturen an;
B
das Volumen welches 100 Kubikzentimeter Gasbei denselben anzunehmen
streben;
C
das aus dem Gefäße ausgestoßene Volumen beider Temperatur des
Gefäßes;
D
dasselbe Volumen auf 0° reducirt;
E
die Volumen-Differenzen für je 100° Temperatur;
F
den erforderlichen Druck um das ausgedehnteVolumen auf 100 K. C. zu
comprimiren, wobei
G
derselbe Druck unter Abzug von 760 Millim.Barometerstand ist;
H
Druck-Differenzen für je 100°.
A.
B.
C.
D.
E.
F.
G.
H.
0°
100
0
0
760
0
100°
136,65
36,65
26,820.
1038,55
278,55
200°
173,30
73,30
42,239
15,419
1317,1
557,1
278,6
300°
209,95
109,95
52,369
10,130
1595,6
835,6
278,5
400°
246,60
146,60
59,449
7,080
1874,1
1114,1
278,5
500°
283,25
183,25
64,695
5,246
2152,7
1392,7
278,6
600°
319,90
219,90
68,740
4,055
2431,2
1671,2
278,5
700°
356,55
256,55
71,953
3,213
2709,8
1949,8
278,6
800°
393,20
293,20
74,568
2,615
2988,3
2228,3
278,5
900°
429,85
329,85
76,734
2,166
3266,8
2506,8
278,5
1000°
466,50
366,50
78,563
1,829
3545,4
2785,4
278,6
1100°
503,15
403,15
80,124
1,561
3823,9
3063,9
278,5
1200°
539,80
439,80
81,474
1,350
4102,4
3342,4
278,5
1300°
576,45
476,45
82,651
1,177
4381,0
3621,0
278,6
Aus diesen Rechnungsresultaten ist ersichtlich, daß bei Beobachtung der ausgestoßenen
Volumina die Differenz für 1° Temperatur bei 1300° nur noch 1,177/100
= 0,01177 Kubikcentimeter wird, ein Volumen das selbst mit den vollkommensten
Meßapparaten nicht mehr bestimmt werden kann, und daß daher diese Methode für höhere
Temperaturen sich nicht eignet; denn wenn auch die Capacität des Gefäßes statt 100
K. C. 500 K. C. wäre, so würde diese Differenz für 1° Temperatur zwar 0,0589
K. C. werden, welches Volumen aber ebenfalls kaum meßbar ist und außerdem müßte die
Capacität der Meßröhre, welche im vorigen Falle 82 bis 85 K. C. war, 413 bis 420 K.
C. werden, wodurch die Bestimmung von 0,0589 K. C. wieder um so viel schwieriger
wird.
Weit günstigere Resultate würde die Methode der Druck-Bestimmung geben, indem
der Druck durch alle Temperaturen gleichmäßig pro
1° Temperatur um 278,6/100 = 2,786 Millimeter wächst. Aber bei der Temperatur
1300° müßte das Manometer eine Quecksilbersäule von 3,621 Meter, beinahe 5
Atmosphären, tragen; dieß wäre nicht nur äußerst unbequem und unpraktisch, sondern
es läßt sich auch gar nicht erwarten, daß das Gefäß auf welches die Temperatur
wirkt, unter solchem Drucke dicht bleiben oder seine Form, also seine Capacität,
beibehalten würde.
Eine Combination dieser beiden Methoden, wie sie Becquerel
angewandt hat, vermeidet zwar diese Extreme, aber sie wird immer noch nicht
hinlänglich genaue Resultate geben, da 400 Millim. Manometerdruck der größte Werth
ist, den wir veranlassen dürfen, aus Gründen, die wir anzuführen alsbald Gelegenheit
haben werden.
Es gibt nun aber noch eine vierte Methode, welche offenbar viel sicherere und
genauere Beobachtungen geben muß, und deren Becquerel
erwähnt, von der er aber merkwürdiger Weise keinen Gebrauch machte. Sie besteht
darin, daß man das Gas in dem Gefäße im erwärmten Raume sich frei ausdehnen läßt,
bis man sich der Temperatur nähert, welche man messen will, und dann die Verbindung
mit der Manometer-Meßröhre herstellt. Das in die Meßröhre austretende Volumen
wird in diesem Falle verhältnißmäßig klein werden, erlaubt daher auch eine enge
Meßröhre anzuwenden, in welcher bei 1/2 Quadrat-Centimeter Querschnitt 1
Millim. Höhe = 0,05 K. C. mißt.
Es ist dabei nur nöthig, bei gleich bleibender Temperatur das ausgestoßene Volumen
unter zwei verschiedenen Drucken zu beobachten.
Wir wollen nun zunächst den Apparat Fig. 3 und 4 beschreiben, welcher zu
solchen Messungen dient.
V ist das Gefäß, welches in den Raum eingeführt wird,
worin sich das Gas ausdehnen soll; die von demselben ausgehende Röhre m, welche in den Dreiweghahn 0 eingekittet ist, muß
möglichst capillar seyn, da die Temperatur des darin eingeschlossenen Gases nicht
genau bestimmt werden kann und daher leicht Irrthümer entstehen könnten, wenn dieses
Volumen groß wäre.
Die kurze Röhre r, welche von dem Hahne ausgeht, dient
dazu, den Apparat durch eine Kautschukröhre mit einer Luftpumpe oder einem
Gasreservoir in Verbindung zu bringen.
Die zwischen dem Hahn o und der Meßröhre a befindliche Röhre ist von Glas und ebenfalls von
möglichst kleinem Durchmesser.
Die Meßröhre a wird am zweckmäßigsten von 8 Millimeter
innerem Durchmesser genommen werden, was ungefähr dem Querschnitte 0,5
Quadrat-Centimeter entspricht, und machen wir deren Länge 33 bis 35
Centimeter, so wird dieselbe ein Volumen von 15 K. C. fassen, dessen Bruchtheile
sich bis 0,05 K. C. genau bestimmen lassen.
Diese Meßröhre a steht mit dem eisernen Dreiweghahn z in Verbindung und durch diesen mit der
Manometer-Röhre b, wie Fig. 3 zeigt.
Die Beobachtungen werden genauer, wenn man der Meßröhre a
und der Manometer-Röhre b denselben Durchmesser
gibt, weil dann der convexe Quecksilberspiegel in der Meßröhre die Concavität des
Spiegels in der Manometer-Röhre aufhebt.
Die Länge der Röhren a und b
soll nicht 33 bis 35 Centimeter übersteigen, weil bei größerer Länge die Temperatur
derselben nicht genau gemessen werden könnte. Um die Temperatur genau messen zu
können, sind die Röhren a und b mit einer nicht unbedeutenden Menge Wasser umgeben. Genaue
Bestimmung der Temperatur dieser Röhren ist aber eine wesentliche Bedingung für die
Operation selbst, denn ohne diese ist es weder möglich das Gasvolumen in der
Meßröhre genau zu bestimmen, noch kann die Quecksilbersäule in der
Manometer-Röhre richtig auf 0° zurückgeführt werden, was unumgänglich
nothwendig ist.
Ein eingehängtes genaues Thermometer, welches in 1/5° getheilt ist, dient zum
Ablesen dieser Temperatur.
Die scheinbare Ausdehnung des Quecksilbers in Glas ist 0,00013135, daher dient die
Formel: h₁ = h/(1 +
0,00013135 . t') in welcher h die beobachtete Höhe der Quecksilbersäule und t die Temperatur des Wassers ist, zur Reduction dieser
Säule auf 0°.
Hätte z.B. diese Säule 300 Millim. Höhe und die Temperatur
des Wassers wäre 23,7°, so ist die reducirte Höhe h₁ = 300/(1 + 0,00013135 . 23,7) = 299,07 Millim.; diese Differenz
von beinahe 1 Millim. darf nicht vernachlässigt werden.
Das zur Ausdehnung bestimmte Gefäß V wurde früher aus
Platin angefertigt; es scheint aber nach den Untersuchungen von Deville und Troost sich
dasselbe nicht dicht zu verhalten und die eingeschlossene Luft sowohl chemisch als
dem Volumen nach verändert zu werden, daher fertigt man dieses Gefäß aus innen und
außen glasirtem Porzellan oder auch aus Eisen an; in letzterem Falle ist jedoch das
Gefäß nicht mit atmosphärischer Luft, sondern mit Stickstoff zu füllen.
Ist dieses Gefäß von Porzellan, so muß die Capillarröhre m ebenfalls von Porzellan gemacht und vermittelst des
Knallgas-Gebläses in dem Halse des Gefäßes fest gelöthet werden.
Ehe die Capillarröhre in dem Halse des Gefäßes V
befestigt wird, ist die Capacität des letzteren nach bekannten Methoden genau zu
bestimmen.
Die Capacität der Capillarröhren m und n darf nicht mehr betragen als 1/200 derjenigen des
Gefäßes V, wenn die Temperatur-Bestimmungen genau
ausfallen sollen.
Nehmen wir an, das in den Capillarröhren m und n enthaltene Gas habe die mittlere Temperatur zwischen
der Temperatur des Gefäßes V und der Meßröhre a; erstere sey 1300° und letztere 20°, so
ist die mittlere Temperatur = t₁ = 660°.
Bezeichnen wir mit f den kubischen
Ausdehnungs-Coefficienten des Eisens = 0,0000355, mit k denjenigen des Glases = 0,000025.
Es seyen ferner, wie in dem Apparate von welchem Becquerel
Gebrauch machte, die
Capacitäten der Röhren m und n bei 0° = 0,60 und 0,15 K. C., so wird deren Inhalt bei der
mittleren Temperatur t₁
Textabbildung Bd. 177, S. 101
folglich das Gasvolumen in beiden Röhren zusammen = 0,224198
K. C., eine Quantität, welche unmöglich vernachlässigt werden darf, weil sie über 4
mal so groß ist als der Beobachtungsfehler bei 8 Millim. weiten Röhren = 0,05 Kub.
Cent.; muß aber dieser Quantität Rechnung getragen werden, so wird dadurch die
Berechnung der Beobachtungsresultate unendlich viel länger und complicirter. Ich
verdanke es den Bemühungen des Hrn. J. Fink in Straßburg,
daß ich diese schleppende Rechnung umgehen kann, indem er mir diese Capillarröhren
von Eisen und von Messing mit bloß einem halben Millimeter innerem Durchmesser durch
Ziehen gebohrter dickerer Röhren herstellte. Dadurch ist der Inhalt der Röhre m bei 0° auf 0,05²π × 30 = 0,0585 Kub. Cent. und derjenige der Röhre n = 0,05²π
× 10 = 0,0195 Kub. Cent. reducirt worden, und das Gasvolumen in denselben bei
der Temperatur t₁ = 660 ist:
Textabbildung Bd. 177, S. 101
also noch nicht einmal halb so groß als der Beobachtungsfehler
von 0,05 Kub. Centimeter.
Nun ist unter Vernachlässigung des äußerst kleinen Volumens in den Röhren m und n, der Inhalt des
Apparates bei 760 Millim. Barometerstand und 0° Temperatur
Textabbildung Bd. 177, S. 101
wenn T die Temperatur im Gefäße
V bezeichnet, v das
Volumen in der Meßröhre a und t die Temperatur des Wassers, welches dieselbe umgibt; d₀ die Dichte des eingeschlossenen Gases und p = h + B, wo h = der auf 0°
reducirten Quecksilbersäule in der Röhre b und B = dem ebenfalls auf 0° reducirten
Barometerstande.
Wird nun die Quecksilbersäule in b erhöht und dadurch das
Volumen v bei gleich bleibender Temperatur zu a = v₁, d.h. kleiner,
so wird h₁ + B = p' und der Inhalt des Apparates stellt sich dar
durch
Textabbildung Bd. 177, S. 101
Machen wir diese beiden Ausdrücke gleich, und eliminiren wir gleiche Factoren, so
wird
Textabbildung Bd. 177, S. 102
Wäre z.B. die Capacität des Gefäßes V bei 0° = 100
Kub. Cent. und wir schließen den Hahn o in dem Momente
wo der Apparat 40 K. C. Gas von 0° enthält, erwärmen aber diese auf
1000°, so werden sie das Volumen 40 . (1 + a
1000) = 186,600 K. C. einnehmen. Die Capacität des Gefäßes V wird bei dieser Temperatur V . (1 + fT) = 100 . (1 + 0,0000355 . 1000) = 103,55 K. C.,
folglich enthält das Gefäß V = 103,550 K. C. Gas und
186,600 – 103,550 = 83,050 K. C. sind in die Meßröhre a ausgestoßen. Da sie aber in dieser Röhre, wie wir annehmen wollen, auf
20° abgekühlt werden, so ist das Volumen des Gases in derselben nicht mehr
83,050, sondern auf 0° reducirt = 83,050/(1 + a .
1000) = 17,803, dann auf die Temperatur des die Meßröhre umgebenden Wassers von
20° = 17,803 (1 + a 20) = 19,108. Da aber die
Röhre a selbst sich durch die Temperatur 20°
ausdehnt, so ist scheinbar das Volumen 19,108/(1 + ft) =
19,108/(1 + 0,00025 . 20) = 19,099 = v. Dabei ist
angenommen, daß das Ganze unter dem normalen Barometerstande von 760 Millim. gewesen
sey; bringen wir nun die 186,600 K. C. Gas von 1000° unter 1060 Millim.
Quecksilberdruck, so wird deren Volumen (186,600 . 760)/1060 = 133,790 K. C. und in
die Meßröhre a gelangen 133,790 – 103,550 =
30,240 K. C.; diese zuerst auf 0° reducirt = 30,240/(1 + a 1000) = 6,482, dann auf die Temperatur des Wassers =
6,482. (1 + a 20) = 6,957 und wegen der Ausdehnung der
Meßröhre selbst = 6,957/(1 + 0,000025 . 20) = 6,954 = v'.
Führen wir nun diese Werthe in obige Formel ein, so erhalten wir
Textabbildung Bd. 177, S. 102
Hätten wir das Gasvolumen im Gefäße V bei 100 K. C.
belassen, so würde
dasselbe bei 1000° = 466,5 geben und in die Meßröhre würden gelangen 466,5
– 103,55 = 362,95 von 1000° = 77,801 bei 0° = 83,505 bei
20°, welche = 83,464 = v wegen Ausdehnung des
Glases; unsere Meßröhre müßte folglich eine Capacität von über 100 Kub. Cent. haben,
um damit Temperaturen über 1000° bestimmen zu können.
Eine Meßröhre aber, welche 100 K. C. faßt und nicht länger als 30 Centimeter seyn
darf, würde einen Querschnitt von 3,333... Quadrat-Centimetern erfordern und
ein Kubikzentimeter würde in dieser Röhre nur eine Höhe von 0,333... Millimetern
einnehmen, so daß die Beobachtungen höchstens auf 1 Kub. Centm. genau werden
könnten, eine Quantität, welche ganz und gar unzulässig ist.
Daraus geht hervor, wie unendlich viel sicherer und genauer diejenige Methode ist,
wobei man das Gasvolumen für jeden Versuch anders nehmen kann.
Um zu jeder Zeit das Volumen des Gases wechseln zu können, dient die Woulf'sche Flasche i, i (Fig. 3), welche
Schwefelsäure enthält, über die das in der Thierblase k
enthaltene Gas streichen muß, um in den Apparat zu gelangen; die Figur zeigt wie
diese Flasche durch ein Kautschukrohr mit dem Hahn o
verbunden ist. In dem Momente, wo der Hahn o so gedreht
wird, daß nur noch V und a
mit einander communiciren und die Flasche i
abgeschlossen wird, steht das Quecksilber in a und b gleich und man kann also leicht vor Schluß des Hahnes
das Volumen v in a nach
Belieben größer oder kleiner nehmen.
Es ist nothwendig, daß der Apparat absolut trockenes Gas enthalte, da die Elasticität
des Wasserdampfes erstens der Temperatur nicht proportional ist und zweitens
unendlich viel größer als diejenige der Gase.
Deßhalb wird zum ursprünglichen Füllen des Apparates zwischen dem Hahn o und der Flasche i eine
kleine Luftpumpe eingeschaltet, der Inhalt von V öfter
leer gepumpt und dann wieder aus der Flasche k gefüllt;
zu diesem Zweck ist die Luftpumpe mit zwei Hahnen versehen, um sie gegen die Flasche
i hin absperren zu können, wenn in V das Vacuum gemacht werden soll.
Was die Größe des Gefäßes V anbetrifft, so ist es
natürlich um so vortheilhafter je größer dasselbe wird, da alsdann die Differenzen
v – v' oder p'
– p, welche bestimmend sind, um so größer
ausfallen.
Wäre z.B. diese Capacität statt 100 K. C. = 200 K. C., so würde der Werth v – v' statt 12,145 =
21,253 bei gleichem Manometerstand, wodurch natürlich die Beobachtung schärfer
wird.
Bei der Capacität 200 K. C. würde sich berechnen v zu =
27,469 und v' zu = 6,216;
bei der Capacität 100 K. C. würde sich berechnen v zu =
19,117 und v' zu = 6,961;
da aber unsere Meßröhre nur noch 0,05 K. C. zu beobachten
gestattet,
so würden die Beobachtungen
etwa
v = 27,5
u. v' = 6,25
für
v = 19,15
u. v' = 7,00 gegeben
haben, und substituiren wir diese Werthe in der Formel, so
gibt das Rechnungsresultat für V = 200 Kub. Cent. =
1001° Temperatur und für V = 100 K. C. =
1005°.
In der Wirklichkeit wird zwar das Volumen in der Meßröhre immer so gewählt, daß man
keine Bruchtheile von Kubikcentimetern hat, da aber auch dabei Beobachtungsfehler
von 0,05 K. C. vorkommen können, so wird immerhin das Resultat um so genauer, je
größer die Capacität des Gefäßes V ist. Das von mir
angewandte Gefäß faßt 246 Kubikcentimeter.
Um nun das thermoelektrische Paar genau in dieselbe Temperatur zu bringen, durch
welche das Gas in V ausgedehnt wird, legt man dasselbe
in die eiserne Röhre x, x, welche in das Gefäß V eindringt.
An die Enden der Platin- und Eisendrähte sind feine gezogene Kupferröhrchen so
fest aufgesteckt, daß sicherer Contact stattfindet, und diese Verbindungsstellen
sind in enge Glasröhren eingesteckt, die in dem würfelförmigen Gefäße W mit Wasser umgeben sind, dessen Temperatur durch ein
gutes Thermometer bestimmt wird. Becquerel hat diese
Verbindungsstellen ebenfalls in Glasröhren gebracht, dieselben aber statt mit Wasser
mit Eis umgeben; dieß hat allerdings den Vortheil, daß die Temperatur ohne
Correction erhoben wird, aber in der Praxis könnte es oft an Eis fehlen und daher
habe ich Wasser vorgezogen. Es genügt, die gefundene Temperatur um so viel kleiner
zu setzen, als die Temperatur des Wassers in W
beträgt.
Die Messingscala g, g, welche die Volumina der Meßröhre
a angibt, ist natürlich fest, die Scala h, h hingegen verschiebbar; letztere wird mit ihrem
unten liegenden Nullpunkte so weit hinauf geschoben, bis dieser mit dem Stand des
Quecksilbers in der Meßröhre a in eine Linie fällt und
dann kann die Höhe der Quecksilbersäule in der Manometer-Röhre b direct an der Scala h, h
abgelesen werden.
Da die elektromotorischen Eisen- und Platindrähte nicht bloß an ihrer, der zu
messenden Temperatur zugekehrten Verbindungsstelle eine höhere Temperatur annehmen,
sondern auf eine gewisse Länge davon afficirt werden, so entsteht daraus eine
Fehlerquelle, weil durch Temperatur-Erhöhung die Leitungsfähigkeit dieser
Drähte für den elektrischen Strom bedeutend vermindert wird.
Der Platindraht von 2 Millimeter Durchmesser hat z.B. bei 13,5° Temperatur den
Widerstand 3,638432, wird aber dessen mittlere Temperatur = 800°, so wird
dieser Widerstand : 3,638432 . (1 + 0,001861 . 800) = 10,065339, wodurch also der
Strom bedeutend geschwächt wird.
Der Eisendraht von 8 1/2 Millimeter Durchmesser hat bei 13,5° Temperatur den
Widerstand: 0,14209 und bei 800° = 0,33232.
Um nun diese Fehlerquelle unwirksam zu machen, ist es nothwendig, den Leitungsdrähten
zwischen dem Rheometer und den elektromotorischen Drähten ebenfalls einen großen
Widerstand zu geben, wodurch der Normal-Widerstand gleichförmiger wird. Haben
diese Leitungsdrähte von Kupfer 1 Millimeter Durchmesser, so ist ihr Widerstand bei
13 1/2° C. und pro 1 Meter Länge = 1; haben
dieselben 1,1 Millim. Durchmesser, so ist er = 1,06.
Würde daher die Gesammtlänge des Leitungsdrahtes nur 1 Meter seyn und dessen
Durchmesser 1,1 Millim., so wäre der Gesammt-Widerstand der Kette bei
13,5° = 3,638432 + 0,142090 + 1,06 = 4,840522 und bei der Temperatur der
elektromotorischen Drähte von
800° = 10,665339 + 0,33232 + 1,06 = 11,457659.
Geben wir aber dem Leitungsdrahte von 1,1 Millim. Durchmesser 20,26 Meter Länge, so
wird der Gesammt-Widerstand der Kette bei 13 1/2° = 3,638432 +
0,142090 + (20,26/1,06) = 22,893729 und bei 800° Temperatur 10,065339 +
0,33232 + (20,26/1,06) = 29,510866, und die Quotienten dieses Widerstandes sind
22,893729/4,840522 = 4,7308, und 29,510866/11,457659 = 2,5758.
Somit wird durch die Verlängerung der Kette der Fehler beinahe um die Hälfte
kleiner; da nun aber die Windungen um den Rheometerrahmen noch hinzukommen, so wird
dieser Quotient in Wirklichkeit:
Textabbildung Bd. 177, S. 105
was sich schon eher ausgleicht und um so mehr genügt, wenn die
elektromotorischen Drähte so in den Raum eingetaucht werden, daß sie sich annähernd
auf gleiche Länge erwärmen.
Diese Nothwendigkeit langer Leitungsdrähte gewährt den Vortheil, daß das
Torsions-Rheometer in großer Entfernung von dem heißen Ofen, an welchem man
experimentirt, aufgestellt werden kann.
Da die elektromotorische Wirkung von der physikalischen Beschaffenheit der die Kette
bildenden Metalle abhängt, so ist es durchaus nothwendig, daß stets dieselben
identischen Metallstäbe oder Drähte zur Bestimmung der Temperatur verwendet werden,
denn verschiedene Drähte, die von ein und derselben Rolle abgeschnitten sind, können
sich wesentlich anders verhalten und müssen genau auf ihre Stromstärke geprüft
werden, ehe sie zur Messung von Temperaturen dienen können.
Folgendes ist nun die Methode, um das Verhältniß der Stromstärke zur Temperatur
festzustellen.
Das thermoelektrische Element wird, wie in Figur 3, in die Röhre x, x gebracht und mit dem Torsions-Rheometer
verbunden. Man erwärmt nun das Gefäß V sehr allmählich
durch glühende Kohlen, welche man in den Ofen A, A
bringt, und stellt den Hahn o wie in der Figur, so daß
das aus V durch die Temperatur ausgestoßene Gas nach der
Blase k gedrängt wird, während in a und b das Quecksilber im Niveau bleibt.
Man schiebt den Zeiger f, f, welcher ursprünglich auf
0° auf dem Theilkreise stand, so vorwärts, daß die astatische Nadel k, k annähernd auf dem Nullpunkte der Gradbogen p, p bleibt.
Nach einiger Uebung gelangt man leicht dahin, durch die Menge der Kohks im Ofen und
durch Verengerung oder Erweiterung der Luftzutritts-Oeffnung constante
Temperaturen zu erhalten.
Man erkennt, daß die Temperatur constant geworden, wenn die Nadel k, k auf demselben Punkte bleibt, ohne daß man den
Zeiger f, f verrückt.
Man notirt alsdann die Zahl der Grade, welche der Zeiger f,
f auf dem Theilkreise D, D anzeigt, die
Temperatur der Luft des Raumes in dem der Apparat steht = t und die Temperatur des Wassers im Gefäße W =
t₀, da mittelst dieser die wirkliche
Stromintensität berechnet werden muß.
Man dreht nun den Hahn o so, daß V mit der Meßröhre a verbunden, die Verbindung
mit i und k hingegen
aufgehoben wird.
Ist nun die Temperatur wirklich constant geworden, so wird auch das Quecksilber in
den Röhren a und b auf
gleichem Niveau stehen bleiben. Am bequemsten ist es, vor der Stellung des Hahnes
o durch den Hahn z so
viel Quecksilber abzulassen, daß in der Röhre a gerade
13 Kub. Cent. Gas enthalten sind, und dieser Stand der Meßröhre = v wird notirt, ebenso der Stand der
Manometer-Röhre = h, welcher, wenn wir so
operiren, gleich Null ist.
Man gießt nun vorsichtig in die Röhre b Quecksilber, bis
das Volumen in a = v' nur
noch 1 Kubikcentimeter ist. Um dieß zu bewirken, wird aber der Quecksilberspiegel in
b höher stehen als in a;
man zieht nun den Maaßstab h, h in die Höhe, bis sein
Nullpunkt auf dem Theilstriche 1 der Scala g, g, welche
das Volumen anzeigt, einsteht, und liest dann die Höhe der Quecksilbersäule in b über diesem Punkt ab, die = h' ist.
Endlich liest man noch die Temperatur des Wassers ab, das die Röhren a und b umgibt = t₀.
Hätten wir nun z.B. v = 13; v' = l; h = 0; h' = 125 Millimeter; t₀ = 21,2° und den Barometerstand 746,78 Millimeter bei
0°: so reduciren wir h' = 125 Millimeter auf
0° = 125/(1 + 0,00013135 . 21,2) = 124,75 Millim. = h', und die gesuchte Temperatur ist dann
p = h +
B = 746,78
p' = h' + B
= 871,53
Textabbildung Bd. 177, S. 107
Hätten nun die thermoelektrischen Beobachtungen die Werthe
z = 25,5''; t =
20,5°; t₀ = 25,4° und T₂ = 514 gegeben, so ist die auf das elektrische
Paar wirkende Temperatur-Differenz = 775,36 – 25,4 = 750°
gewesen, und dieser entspricht die Stromintensität 377, auf z = 25'' und t = 13,5° reducirt
Textabbildung Bd. 177, S. 107
Da die thermoelektrischen Stromintensitäten keineswegs den Temperaturen welche sie
hervorgebracht haben, proportional sind und sogar sehr viele Unregelmäßigkeiten
zeigen, so ist es nothwendig solche Versuche für nicht sehr entfernte
Temperatur-Intervalle anzustellen, um dadurch das Gesetz dieser
Stromintensitäten festzustellen.
Ein Beispiel einer solchen Versuchsreihe wird diese Bestimmung am besten klar
machen.
Die wirksamen Temperatur-Differenzen waren:
483,6; 584,85; 615,8;
661,74; 780,86; 867,1;
885,75 und 997,5° C. = T
die denselben entsprechenden Stromintensitäten oder
Rheometer-Anzeigen auf 13,5° Temperatur und 25 Secunden
Oscillationsdauer = z =
207,50;
233,99; 264,90;
294,64; 376,73;
472,99; 505,73
und 655,33 = J
die Quantitäten J/T =
0,42909; 0,40009; 0,43017; 0,44528; 0,48246;
0,54548; 0,57097 und 0,65698 = R.
Die Differenzen dieser Quotienten geben, durch die Temperatur Differenzen dividirt, =
(R – R')/(T – T') = B
0,00028643; 0,00096951;
0,00032891; 0,00031141; 0,00073076;
0,0013677 und 0,0008867.
Aus den Werthen R ist ersichtlich, daß bei den hier
gewählten Metallen und bei der Beschaffenheit derselben die Stromintensität zwischen
den Temperaturen 207,5 und 233,99 abnimmt und dann wieder ohne große Regelmäßigkeit
zunimmt.
Um nun diese Werthe in eine Reihe zu bringen, hat Becquerel die Formel:
J = TA +
T²B
gewählt, welche wohl hinlänglich genau und bequem ist.
Stellen wir diese Versuchsreihe zusammen, so ergibt sich:
T
J
J/T = R
Differenzen.
B
A
für dieTemperatur-Intervalle.
483,6
207,50
0,42909
584,85
233,99
0,40009 –
0,02900
0,00028643
0,56759
483,6 und 584,85
615,8
264,90
0,43017
0,03008
0,00096951
0,16692
584,85 und 615,8
661,74
294,64
0,44528
0,01511
0,00032891
0,22764
615,8 und 661,74
780,86
376,73
0,48246
0,03718
0,00031141
0,23617
661,74 und 780,86
867,1
472,99
0,54548
0,03302
0,00073076
0,08816
780,86 und 867,1
885,75
505,73
0,57097
0,02549
0,00136770
0,63962
867,1 und 885,75
997,5
655,33
0,65698
0,08601
0,0008867
0,11077
885,75 und 997,5.
Rechnen wir darnach die Reihe für je 50° Temperatur-Differenz, und
nehmen wir an, die letzten Werthe von A und B erstrecken sich bis 1400° Temperatur, so ergibt
sich:
T
J
T
J
500°
212,20
1000°
658,91
550°
225,53
1050°
732,26
600°
248,87
1100°
809,45
650°
286,92
1150°
890,52
700°
317,91
1200°
975,38
750°
352,30
1250°
1064,15
800°
397,15
1300°
1156,71
850°
453,04
1350°
1253,17
900°
523,73
1400°
1353,53
950°
589,39
Da der Zweck eines solchen Pyrometers der ist, Temperaturen zu messen, welche weit
über 500° gehen, so kann man sich auf die Graduirung zwischen 500° und
1300° beschränken; weiter zu gehen, wird wohl kaum möglich seyn, da das
Gas-Ausdehnungsgefäß, welches zur Graduirung dient, über 1300°
erhitzt, seine Form verlieren und seine Capacität ändern dürfte, bei jedem Material
woraus dasselbe angefertigt seyn möchte.
Bisher ist es nicht einmal möglich gewesen, die Graduirung über 1000°
auszudehnen, da das Luftpyrometer, trotz aller Sorgfalt bei dessen Construction,
über diese Temperatur hinaus undicht wird, daher auch die Werthe J in vorstehender Tabelle über 1000° hinaus
unsicher sind.
Um wo möglich die Graduirung noch auf höhere Grade ausdehnen zu können, werde ich
versuchen das Gasreservoir des Luftpyrometers so zu construiren, daß alle
Verbindungsstellen außerhalb des Ofens reichen, so daß die Ausdehnung des Metalles
nicht mehr schädlich einwirken kann.
Obgleich Deville und Troost das
Porzellan als das einzige brauchbare Material zur Anfertigung von Gaspyrometern
erklären, sind auch sie nicht über 1000° hinausgegangen, und jedenfalls hat
das eiserne cylindrische Reservoir den großen Vorzug, daß ihm eine viel größere
Capacität gegeben werden kann; ferner ist eine Endosmose bei der Beobachtungsweise
mit veränderlichen Gasquantitäten weit weniger zu fürchten als bei der bisher
üblichen Methode, und was mich endlich noch am meisten für das eiserne Reservoir
bestimmt, ist die Möglichkeit, eine sehr capillare Verbindungsröhre mit dem
manometrischen Apparate anzuwenden, welche deren Capacität zu vernachlässigen
gestattet; denn wenn diese Röhre einen größeren inneren Querschnitt hat und das
Reservoir eine viel kleinere Capacität, so werden die Messungen trotz aller
Corrections-Rechnungen doch nie genaue Resultate geben.
Bei Pressungen von 150 Millimet. Quecksilber im Maximum, wird auch die Deformation
des cylindrischen eisernen Reservoirs kaum mehr zu fürchten seyn als bei
Porzellan.
Auch ist das Einschieben des thermoelektrischen Paares nur bei eisernen, nicht bei
porzellanenen Reservoirs möglich.
Um nun durch die Stromintensität des thermoelektrischen Pyrometers die Temperatur
erkennen zu können, ist es am bequemsten, aus einer solchen Versuchsreihe die
Intensität für alle Temperaturgrade zu berechnen und daraus eine Tabelle zu bilden,
in welcher man die gefundene und auf z = 25'' und t = 13,5° reducirte Intensität aufschlägt und der
daneben stehenden Temperatur die Temperatur t₀
zufügt.
Becquerel hat auch die Methode eingeschlagen, das
thermoelektrische Pyrometer durch die Schmelzpunkte und Siedepunkte einiger Metalle zu bestimmen,
welche Punkte zuerst durch das Gas-Pyrometer bestimmt waren. Da er aber nur
Gold und Silber im chemisch reinen Zustande hatte, so ist diese Methode wenigstens
einstweilen ganz unzuverlässig; sie könnte aber sehr bequem seyn, wenn man ganz
reine Metalle dazu verwenden würde, deren genaue Schmelz- und Siedepunkte bis
jetzt noch nicht bekannt sind.
Es verdient indeß doch die Methode Erwähnung, durch welche Becquerel die Schmelzpunkte von Silber, Gold und Kupfer bestimmte, denn
ich glaube er ist der erste, welcher dazu den richtigen Weg einschlug.
Wenn auch die Leitungsfähigkeit der meisten Metalle sehr groß und deren latente
Schmelzwärme sehr klein ist, so ist doch für das kleinste Korn dieser Metalle immer
eine gewisse Zeit erforderlich, ehe dasselbe in der ganzen Masse eine gleichförmige
Temperatur angenommen hat und es kann daher die Temperatur in dem Momente, wo man
die Flüssigkeit dieser Masse erkennt, schon eine höhere geworden seyn als diejenige
war, welche diesen Zustand herbeiführte.
Ferner ist es äußerst wahrscheinlich, daß alle schmelzbaren Körper durch den Einfluß
der Wärme wenigstens für einen Moment in den breiartigen Zustand übergehen, ehe sie
wirklich flüssig werden; das Eisen z.B. nimmt diesen Zustand sogar zwischen einem
sehr großen Temperatur-Intervall an, bis es völlige Flüssigkeit erlangt, und
der Uebergang vom breiartigen Zustand in den flüssigen ist unter gewöhnlichen
Umständen nicht wahrnehmbar.
Alle diese Unbestimmtheiten und Unsicherheiten verschwinden, wenn man, wie Becquerel gethan hat, die zu schmelzende Substanz als
feinen Faden oder Draht anwendet, diesen in einer Muffel aufhängt und die Temperatur
so langsam steigert, daß man den Moment wahrnehmen kann, wo der Faden sich zu
verkürzen anfängt, bis er nach einigen Secunden gänzlich abgeschmolzen ist, ohne daß
sich die Temperatur in dieser Zeit merklich ändert.
Will man das thermoelektrische Pyrometer durch solche Schmelzpunkte graduiren, so ist
es durchaus nothwendig, daß das Ende des thermoelektrischen Paares so nahe als
möglich an den verticalen Faden, in der Mitte seiner Höhe, hinrage.
Dazu ist nun allerdings das Platin-Eisen-Paar weniger geeignet, denn
man kann dasselbe ohne Umhüllung nicht in eine Muffel bringen, ohne daß das Eisen
sich bedeutend oxydirt; es muß dasselbe in eine eiserne oder thönerne Röhre
eingesenkt und in dieser mit Sand umgeben werden, und dann ist es noch fraglich ob die Temperatur
des Pyrometers derjenigen des schmelzenden Metalles ganz identisch sey.
Pouillet hat das Platin-Eisen-Element mit
einem Flintenlauf construirt, in dessen Schwanzschraube der Platindraht
eingeschweißt war, so daß letzterer mitten durch das Rohr gieng, ohne solches
innerhalb der Schwanzschraube zu berühren. Das in's Feuer gesenkte Ende mit der
Schwanzschraube wurde dann mit feuerfestem Thon überklebt. Da aber ein solcher
Ueberzug leicht springt und wenig Sicherheit gegen rasche Oxydation gewährt, so fand
ich es für besser, das thermoelektrische Element in eine Thonröhre einzuschließen
und in dieser mit Sand zu umgeben.
In den „Relations des expériences entreprises
par ordre de M. le Ministre des travaux publics etc.“ sagt
Regnault, daß die Versuchsresultate mit einem
Platin-Eisen-Element mit demselben Apparate nicht genau gleich
ausgefallen seyen, und er schließt daraus, daß thermoelektrische Ströme zur
Bestimmung von Temperaturen nicht zulässig seyen.
Allerdings gelingt eine genaue Uebereinstimmung nicht immer, da es sehr schwer ist
die Temperatur des thermoelektrischen Paares derjenigen gleich zu machen, welche das
controlirende Gas-Pyrometer oder das schmelzende Metall anzeigt; dieß ist bei
niedrigen Temperaturen weit mehr der Fall als bei höheren, weil die Umhüllung des
thermoelektrischen Elementes um so mehr Zeit braucht als die Temperatur klein ist,
bis sie die Temperatur des Raumes angenommen hat, in die sie getaucht wird; wenn
aber hinreichende Sorgfalt und Geduld verwendet worden, um wenigstens 15 Minuten
eine constante Temperatur zu unterhalten, so werden die Versuchsresultate immer sehr
annähernd gleich ausfallen; und hat man zur Graduirung des thermoelektrischen
Pyrometers die nöthige Sorgfalt nicht fehlen lassen, so ist es dann leicht bei
wirklichen Temperatur-Bestimmungen solche Zahlen zu erhalten, welche der
Wahrheit sehr nahe kommen, indem man die Temperatur längere Zeit auf das Element
einwirken läßt, ehe man die Stromintensität bestimmt.
Uebrigens hat es offenbar bisher auch an einem brauchbaren Meßapparat für die
Stromintensität gefehlt und ohne diesen können derartige Versuche nie gleiche
Resultate geben.
Thermoelektrisches Pyrometer zur
Bestimmung der Temperatur der Ofenwand-Flächen.
Wäre die Wärmeleitungsfähigkeit des Materiales, aus dem unsere Oefen gebaut sind, bei
jeder Temperatur constant, so würde es genügen diese Leitungsfähigkeit ein für
allemal zu bestimmen, und es wäre dann leicht, aus der gefundenen Ofentemperatur den
Wärmeverlust zu berechnen, welcher durch die Ofenwände mittelst Transmission an die
äußere Luft stattfindet.
Da dieß aber nicht der Fall ist, so ist es nothwendig die Temperatur der äußeren
Ofenwand-Flächen genau zu bestimmen, woraus dann die Transmission welche
dieser Temperatur zukommt, sehr leicht und sehr annähernd zu erheben ist.
Es gilt dafür die bekannte Formel von Dulong
Smaφ (a ± 1) + Lntb
und es handelt sich nur darum, die Temperatur der Luft = φ und die der Ofenwand = t₁ zu bestimmen, um den Werth t = t₁ – φ
zu erhalten.
Die Werthe von S sind für fast alle Baumaterialien gleich
3,62,
die Werthe von L wechseln mit der Lage und der Höhe der
transmittirenden Flächen und sind für horizontale Flächen = 1,778 und für verticale
Flächen von
2
3
5
8
12
15 Meter Höhe
L =
2,21;
2,13;
2,05;
1,99;
1,95 u.
1,92
Unter diesen Annahmen habe ich eine Tabelle gefertigt für
Temperatur-Differenzen von 1° bis 400°, so daß man einfach die
Temperatur-Differenz der Ofenwand-Fläche gegen die Luft aufzuschlagen
hat, um die entsprechende Wärmemenge zu finden, welche per 1 Quadrat-Meter Fläche und per
Stunde transmittirt wird.
Da man nicht den Wärmeverlust zu kennen wünscht, der in einem gegebenen Augenblicke
stattfindet, sondern einen mittleren Werth, so ist in dieser Tabelle der Werth φ = 10° C. angenommen; somit ist t stets um 10° niedriger als die Temperatur der
Ofenwand-Fläche.
Wäre letztere z.B. 379°, so ist t = 369; wäre die
Fläche eine verticale von circa 2 Meter Höhe, so finden
wir in der Tabelle den entsprechenden Werth = Smaφ (a ± 1) + Lntb = 7767,7 + 1784,4
= 9552,1 W. E.
Es versteht sich, daß die Wandflächen-Temperatur an verschiedenen Stellen
gemessen werden muß, und daß das Endresultat als Summe von Flächen verschiedener
Temperatur in Rechnung zu bringen ist.
Solche Messungen lassen sich nun sehr leicht durch ein elektromotorisches Element
ausführen, welches so angeordnet ist, daß die elektromotorischen Drähte mit der
Ofenwand in innige Berührung gebracht werden können.
Zu diesem Ende habe ich den Apparat Fig. 5 und 6 construirt. Derselbe
besteht in einem Messingblech-Cylinder, welcher an beiden Enden mit quadratischen Holzscheiben
versehen ist, auf denen der Cylinder horizontal ruht. An der oberen Wölbung des
Cylinders ist eine Dille angebracht, welche einerseits dazu dient, denselben mit
Wasser zu füllen, andererseits ein Thermometer einzusenken das die Temperatur des
Wassers angibt.
Der Achse des Cylinders parallel gehen zwei Glasröhren durch denselben, welche an
beiden Enden um einige Centimeter hervorragen und die elektromotorischen Drähte
aufnehmen. Diese Drähte sind am einen Ende breit geschlagen und mit kleinen Nieten
von einem der elektromotorischen Metalle fest über einander genietet. Dieses flach
geschlagene und übereinander gelegte Stück ist gerade so lang als die Distanz der
beiden Glasröhren, und von da biegen sich die Drähte rechtwinkelig in die Glasröhren
ein und ragen am anderen Ende derselben um 1 Centimeter hervor, um sie durch
Klemmschrauben mit den zum Torsions-Rheometer führenden Leitungsdrähten in
Verbindung zu setzen.
Sind indessen beide Drähte ein anderes Metall als dasjenige der Leitungsdrähte, so
sind beide elektromotorische Drähte innerhalb der Glasröhren mit dem Metalle zu
verbinden, aus dem die Leitungsdrähte bestehen, damit diese Verbindungsstellen die
Temperatur des die Glasröhren umgebenden Wassers annehmen.
Da ich zu diesem Apparate Kupfer und Messing als elektromotorisches Element gewählt
habe und die Leitungsdrähte von Kupfer sind, so ist nur der Messingdraht innerhalb
der Glasröhre durch ein feines Kupferröhrchen verlängert.
Der Cylinder ist von solcher Größe gewählt, daß er mit Wasser gefüllt 2–2 1/2
Kilogramme wiegt; dadurch wird erstens die Wassermenge so groß, daß deren Temperatur
nicht gar zu schnell steigt und zweitens wird der gegen die Ofenwand fest
angedrückte Apparat vermöge seines Gewichtes an seiner Stelle unbeweglich bleiben
und die innige Berührung mit der Ofenwand erhalten.
Ich habe gefunden, daß Kupfer und Messing bei niedriger Temperatur intensivere Ströme
geben als alle anderen Elemente mit Ausnahme von Wismuth und Antimon, die aber,
besonders ersteres wegen seines niedrigen Schmelzpunktes, in diesem Falle sich nicht
eignen würden.
Folgendes ist das Gesetz, nach welchem die Stromintensitäten den Temperaturen folgen,
für diejenigen Drähte aus denen mein Apparat construirt ist.
T
J
J/T
(R – R')/(T –
T')= B
A
für die Intervalle
50
14,652
0,29304
0,0013320
0,22644
=
50 –
100
100
35,964
0,35964
0,0003560
0,32404
100 –
150
150
56,610
0,37740
0,0002108
0,34578
150 –
200
200
77,587
0,38794
0,0000200
0,38394
200 –
250
250
97,235
0,38894
–
0,0004465
0,50057
250 –
295,8
295,8
109,00
0,36894
0,00027716
0,28652
295,8 – 374,6
374,6
146,22
0,39033
Es ist unnütz, hier die Rechnungsresultate mitzutheilen, welche aus diesen
Beobachtungen sich für die Temperaturen zwischen 50 u. 374,6° ergeben, da
jeder andere Draht ähnlicher Metalle einem etwas variirenden Gesetze folgt, daher
Jeder der von einem solchen Apparate Gebrauch machen will, für seine Drähte entweder
selbst oder durch den Mechaniker der ihm den Apparat liefert, das
Stromintensitäts-Gesetz durch Versuche feststellen oder feststellen lassen
muß.
Es versteht sich, daß die beobachtete Torsion wie bei dem
Platin-Eisen-Pyrometer jedesmal auf z =
25'' und t = 13,5° zu reduciren ist und daß die
Temperatur des Wassers im Kühlgefäße von derjenigen abzuziehen ist, welche der
reducirten Stromintensität entspricht.
Das bei der Beobachtung auszufüllende Schema ist also:
die Schwingungszeit der Nadel am Rheometer = z,
die Temperatur des Raumes und folglich der Leitungs- und
Rheometerdrähte = t,
die Temperatur des Kühlwassers, in welches das Element
eingetaucht ist = t₀.
Hätten wir z.B. z = 26'', t =
28°, t₀ = 36° u. T₂ = 136, so ist die auf z = 25'' u. t = 13,5°
reducirte Stromintensität:
Tabelle
A
Log für
28°
=
0,97494 – 1
„
B
„ für
z = 26''
=
0,96594 – 1
Log T₂
=
2,13354
–––––––––
2,07442 = N . 118,69 = J.
Nun entspricht dieser Intensität nach obigen Versuchsresultaten die Temperatur
T =
316°,
von welcher aber
t₀ =
36°
abzuziehen ist.
––––––
Somit ergibt sich
280°
als gemessene Ofenwand-Temperatur.
Zur Messung der inneren Ofen-Temperatur hat man z.B.
z
= 26,5''
= Log
0,98280 – 1
t
= 20,5°
= Log
0,98776 – 1
T₂
= 377°
= Log
2,57634
––––––––
2,54690 = J = 352,29,
welche der Temperatur 750° entsprechen; davon ist aber
der Werth t₀, zu 37° angenommen, in Abzug zu bringen, wodurch die
gemessene Temperatur = 713° wird.
Schließlich habe ich noch dem Herrn Mechanicus Oechsle in
Pforzheim, welcher mich durch die Anfertigung der thermoelektrischen Apparate, und
Hrn. Johann Fink in Straßburg, welcher mich hauptsächlich
bei der Anfertigung der luftpyrometrischen Apparate und dann mit Aufopferung bei den
Versuchen unterstützte, meinen öffentlichen Dank abzustatten.
Straßburg, den 5. Juni 1865.
TabelleA.
Corrections-Coefficienten für den
Leitungswiderstand von Kupferdrähten, Normaltemperatur = 13,5°
C. x = 0,004097.
TemperaturderLuft = t
Log 1/(1 + xt)
TemperaturderLuft = t
Log 1/(1 + xt)
TemperaturderLuft = t
Log 1/(1 + xt)
0
0,02338
12
0,00266
24
0,98171 – 1
0,5
0,02554
12,5
0,00178
24,5
0,98086 – 1
1
0,02169
13
0,00039
25
0,98001 – 1
1,5
0,02084
13,5
0,00000
25,5
0,97916 – 1
2
0,01999
14
0,99911 – 1
26
0,97831 – 1
2,5
0,01914
14,5
0,99822 – 1
26,5
0,97746 – 1
3
0,01829
15
0,99734 – 1
27
0,97662 – 1
3,5
0,01744
15,5
0,99646 – 1
27,5
0,97578 – 1
4
0,01658
16
0,99558 – 1
28
0,97494 – 1
4,5
0,01572
16,5
0,99469 – 1
28,5
0,97410 – 1
5
0,01486
17
0,99381 – 1
29
0,97326 – 1
5,5
0,01400
17,5
0,99294 – 1
29,5
0,97243 – 1
6
0,01314
18
0,99206 – 1
30
0,97159 – 1
6,5
0,01224
18,5
0,99120 – 1
30,5
0,97076 – 1
7
0,01141
19
0,99033 – 1
31
0,96992 – 1
7,5
0,01055
19,5
0,98945 – 1
31,5
0,96910 – 1
8
0,00967
20
0,98859 – 1
32
0,96828 – 1
8,5
0,00880
20,5
0,98776 – 1
32,5
0,96745 – 1
9
0,00794
21
0,98686 – 1
33
0,96662 – 1
9,5
0,00706
21,5
0,98600 – 1
33,5
0,96580 – 1
10
0,00619
22
0,98514 – 1
34
0,96498 – 1
10,5
0,00531
22,5
0,98428 – 1
34,5
0,96416 – 1
11
0,00442
23
0,98342 – 1
35
0,96334 – 1
11,5
0,00354
23,5
0,98256 – 1
TabelleB.
Verhältniß der Quadrate der
Schwingungszeiten zur Correction der beobachteten Torsionsgrade,
Normalzeit = 25 Secunden.
z
Log 25²/z
z
Log 25²/z
z
Log 25²/z
24''
0,03546
26,25
0,95762 – 1
28,50
0,88619 – 1
24,25
0,02646
26,50
0,94939 – 1
28,75
0,87861 – 1
24,50
0,01735
26,75
0,94124 – 1
29
0,87109 – 1
24,75
0,00873
27
0,93316 – 1
29,25
0,86364 – 1
25
0,00000
27,25
0,92515 – 1
29,50
0,85619 – 1
25,25
0,99136 – 1
27,50
0,91722 – 1
29,75
0,84891 – 1
25,50
0,98280 – 1
27,75
0,90936 – 1
30
0,84164 – 1
25,75
0,97433 – 1
28
0,90157 – 1
26
0,96594 – 1
28,25
0,89385 – 1
Tafeln