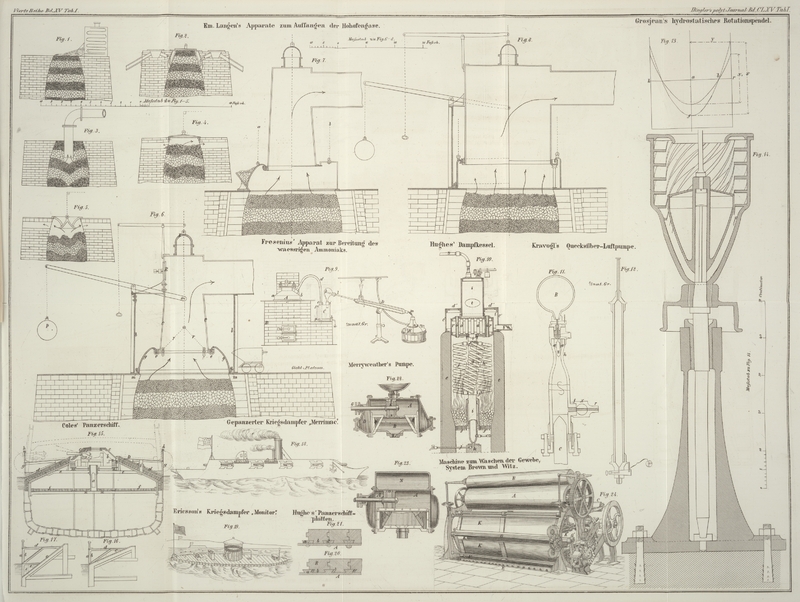
| Titel: | Das hydrostatische Rotationspendel; von L. Grosjean. |
| Autor: | L. Grosjean |
| Fundstelle: | Band 165, Jahrgang 1862, Nr. II., S. 7 |
| Download: | XML |
II.
Das hydrostatische Rotationspendel; von L. Grosjean.
Privilegirt in Oesterreich seit April
1862.
Mit Abbildungen auf Tab.
I.
Grosjean, über das hydrostatische Rotationspendel.
Der bisher am meisten angewendete Apparat um die Geschwindigkeit der Motoren zu
reguliren, ist wohl unstreitig das Watt'sche Kreispendel.
Dasselbe unterliegt aber einem Mangel, den zu beseitigen längst Bedürfniß war,
vorzüglich für Motoren, welche Werke betreiben deren Bewegung eine möglichst
gleichförmige seyn soll.
Wenn auch durch Wahl eines größeren Elongationswinkels das Spiel des Kreispendels dem
eines Franke'schen parabolischen Pendels nahezu
gleichkommt, so bleibt doch ein Hauptmangel zurück, der allen diesen und ähnlichen
Apparaten gemeinschaftlich eigen ist und welcher durch deren Beharrungsvermögen herbeigeführt wird.
Wenn schon zwischen dem Beginn einer von der normalen abweichenden Geschwindigkeit
und deren Zurückführen auf erstere, dem regulirenden Apparat eine gewisse Zeit
gestattet werden muß, so ist es doch von großem Belang diesen Zeitraum auf die
kleinste mögliche Größe zu beschränken. Der Wunsch, diese Grenze zu erreichen, ließ
vorliegendes hydrostatische Pendel entstehen, bei welchem eben das
Beharrungsvermögen der schwingenden Masse benützt wird, um die Regulirung
rechtzeitiger zu bewirken.
Rotirt ein cylindrisches Gefäß, welches auf gewisse Höhe mit einer Flüssigkeit
gefüllt ist, um dessen verticale Achse mit einer Winkelgeschwindigkeit w, so nimmt bekanntlich die vorher in ruhendem Zustande
eine horizontale Ebene bildende Flüssigkeit nun die Oberfläche eines Paraboloids an,
dessen Parameter durch
P = 2g/w² gemessen wird.
Bezeichnet n die Anzahl der Rotationen pro Minute, so wird
P = 2g .
900/n² . π² = 1788 . 94788/n²
(in metrischem Maaß).
Für eine Ordinate y gleich dem Radius des Gefäßes,
nämlich für den höchsten an den Wänden emporgeschleuderten Flüssigkeitsfaden, ist
die zugehörige Abscisse x = y²/P = 0,000558987 . y²
. n², welches die Größe der Denivellation angibt, welche
bei n Rotationen entsteht; für eine andere Rotationszahl
n₁ ist
x₁
= 0,000558987 . y² . n₁² und
daher
x – x₁
= 0,000558987 . y² . (n² – n₁²)
(I)
Es ist nun in die Augen springend, daß das Denivellations-Paraboloid durch die
ursprüngliche horizontale Ebene hr, Fig. 13,
dergestalt geschnitten wird, daß:
1) das Flüssigkeitsvolum, welches an der Gefäßwand über die Horizontale hr geschleudert wird, gleich ist jenem in der
Mitte verdrängten;
2) die Höhe der Hebung an der Gefäßwand gleich ist der Senkung am Scheitel des
Paraboloids.
Hieraus folgt:
af = x/2, ferner
ab = √y²/2 = 0,7071 . y.
Da nun y als Radius des Gefäßes constant ist, so
bezeichnet die Ordinate ab den Radius eines in der
horizontalen Ebene liegenden constanten Kreises, welcher allen möglichen
Denivellations-Paraboloiden gemeinschaftlich ist, und in welchem dieselben
sich alle unter sich und mit der Horizontalen schneiden.
Setzt man innerhalb dieses Kreises einen concentrischen Schwimmer von nahezu
demselben Radius ab, so folgt dieser den Denivellationen die bei verschiedenen
Geschwindigkeiten entstehen, nach Maaßgabe der Bewegung des Schwerpunktes der
verdrängten Flüssigkeit, und ist hiernach das Mittel ein zu regulirendes Organ des
Motors, z.B. die Drosselklappe einer Dampfmaschine, entsprechend zu bewegen. In der
That wirkt dieser Apparat, für den Fall als die Flüssigkeit den Rotationen des
Gefäßes unmittelbar folgt, so sicher als ein in parabolischer Bahn sich bewegender
Schwungkugel-Regulator, weil für jede Winkelgeschwindigkeit eine zugehörige
beharrungsfähige Denivellation nothwendig sich gestaltet, und wird denselben wegen
Wegfall jedes nennenswerten Reibungswiderstandes übertreffen.
Dieß gilt, wie bemerkt, unter der Voraussetzung daß die Flüssigkeit durch irgend eine
Vorrichtung, z.B. ein an der inneren Gefäßwand angebrachtes Schaufelsystem,
gezwungen wird der Bewegung des Gefäßes zu folgen. Indem nun diese Schaufeln an der'
inneren Wand und zwar in radialem Sinne von letzterer bis an den gemeinschaftlichen
constanten Kreis vom Radius ab, reichend, dagegen
in Bezug auf die horizontale Ebene, diese unter einem Winkel von 45°
schneidend angebracht werden, erzeugen dieselben außer dem Mitführen der Flüssigkeit
noch eine andere weitergreifende Wirkung.
Befindet sich nämlich der Apparat in Bewegung und es tritt eine
Geschwindigkeitsänderung ein, z.B. von der normalen Rotation n zu einer geringeren n₁, so wird die Flüssigkeit in Folge ihres
Beharrungsvermögens augenblicklich eine relative Bewegung längs der Gefäßwand
anzunehmen bestrebt seyn, nämlich bestehend in der Differenz zwischen der
vorangegangenen normalen und der nun vorhandenen verminderten Geschwindigkeit. Indem
nun diese in relativer Bewegung begriffene Flüssigkeitsmasse gegen die schiefen
Flächen des Schaufelsystems stößt, wirkt letzteres
denivellirend auf die Flüssigkeit, bevor die Denivellation x₁, welche der Rotation n₁ entspricht, eintreten konnte.
Diese Voreilung ist um so zweckmäßiger, als sie im Verhältniß
mit dem (positiven oder negativen) Momente wächst,
welches ursächlich die Geschwindigkeitsveränderung herbeizuführen im Begriffe
ist.
Um praktische Abmessungen zu erhalten, dient folgende Betrachtung:
Das Volum der in der Mitte durch die Rotation n
verdrängten Flüssigkeit ist
(ab² . π . af)/2 =
y² . π . x/8
und für die Rotation n₁
= y² . π . x₁/8
daher das Volum, welches der Apparat versetzt, wenn dessen
Rotation von n auf n₁
übergeht:
= y² . π . (x – x₁)/8
das Moment dieser Flüssigkeitsversetzung ist daher
W = y² . π . (x –
x₁)/8 × (x – x₁)/3
× γ,
wobei γ das Gewicht eines
Kubikmeters der Flüssigkeit in Kilogr. bedeutet. Es ist daher für Wasser
W
= 130,89969 . . y² (x – x₁)²,
und da nach
(I)
(x –
x₁)
= 0,000558987 . y² . (n² – n₁²) so wird
W
= 0,0000409 y⁶ (n² – n₁²)²
Setzt man für n und n₁
jene Rotationszahlen, deren Differenz genügen soll den Apparat wirksam zu machen,
und für W das Moment, welches die entsprechende
Bewegung des zu regulirenden Organes hervorbringt, so wird
Textabbildung Bd. 165, S. 10
wodurch der innere Radius des Gefäßes bestimmt wird. Aus x ergibt sich die nöthige Höhe desselben.
Um die Wirksamkeit des schief gestellten Schaufelsystems zu würdigen, setze man die
Umfangsgeschwindigkeit des äußersten Wasserfadens pro
Secunde für n Rotationen
v = (2y .
π . n)/60 und für n₁
Rotationen
v₁ = (2y
. π . n₁)/60 daher
v² – v₁² = 0,010966227 . . y² . (n²
– n₁²).
Die Höhendifferenz welche durch den Stoß der relativen Bewegung des
Flüssigkeitsfadens gegen die Schaufeln veranlaßt wird, ist folglich:
Textabbildung Bd. 165, S. 10
d.h. die Höhendifferenz welche augenblicklich durch die Geschwindigkeitsveränderung von n auf n₁
hervorgebracht wird, ist gleich jener Denivellation die auf gewöhnlichem Wege, jedoch später entstehen würde.
Die Formel (II) zeigt, daß für die Anwendung die Größenverhältnisse des Apparates,
daher dessen beanspruchter Raum und Kostenaufwand, um so geringer wird, je größer
bei gleichbleibendem Werthe von W und n/n₁ die
Rotationszahlen n und n₁ an und für sich genommen werden.
Folgende Tabelle, bei welcher W = 0,005k m und n/n₁ = 50/49 angenommen
ist, enthält die Werthe von y, x und x₁ für verschiedene Winkelgeschwindigkeiten.
Rotationenpro
Minute.
Radiusdes Gefäßes.
Denivellat.
Differenz.
I.
n =
80 n₁ =
78,4
y = 0m,4466
x = 0m,4466 x₁ = 0m,4289
x – x₁ = 0m,0157
II.
n = 90 n₁ = 88,2
y = 0m,3266
x = 0m,4829 x₁ = 0m,4638
= 0m,0191
III.
n =
100 n₁
= 98
y = 0m,3045
x = 0m,5182 x₁ = 0m,4977
= 0m,0205
IV.
n =
200 n₁ =
196
y = 0m,19182
x = 0m,82271 x₁ = 0m,79013
= 0m,03258
Für eine Füllung des Gefäßes mit Quecksilber, wofür
Textabbildung Bd. 165, S. 11
und wenn für W und n/n₁ die obigen
Werthe beibehalten werden, gestalten sich folgende Dimensionen für verschiedene
Geschwindigkeiten:
V.
n =
130 n₁ =
127,4
y = 0m,1648
x = 0m,2566x = 0m,2464
x – x₁ = 0m,0102
VI.
n =
140 n₁ =
137,2
y = 0m,1569
x = 0m,2696 x₁ = 0m,2589
= 0m,0107
VII.
n =
150 n₁ =
147
y = 0m,1498
x = 0m,2822 x₁ = 0m,2710
= 0m,0112
VIII.
n =
200 n₁ =
196
y = 0m,1237
x = 0m,3423 x₁ = 0m,3287
= 0m,01355
In Figur 14
ist ein nach Resultat VIII construirtes, mit Quecksilber gefülltes hydrostatisches
Rotationspendel in 1/4 der natürlichen Größe dargestellt, und besteht aus einem
gußeisernen Gefäße, welches auf einer Spindel dicht befestigt ist. Diese Spindel
lagert in einem Ständer, welcher mit Spur und Halslager versehen, ölhaltend, die
Spindel frei rotiren läßt, und seinerseits auf einem Quader des Fundaments
aufgeschraubt ist. Ueber die Verlängerung der Spindel, welche in das Gefäß tritt,
ist der ebenfalls gußeiserne Schwimmer derart aufgesteckt, daß derselbe mittelst
Feder und Nuth an der Spindel leicht auf und ab bewegt werden kann, dagegen an ihrer
drehenden Bewegung Theil zu nehmen gezwungen ist. Der Schwimmer ist an seiner
Tauchungsfläche nach dem Denivellations-Paraboloid geformt, welches der
normalen Geschwindigkeit des Apparates entspricht. Am oberen Ende seiner Hülse ist
auf übliche Weise die Stange eingehängt, welche die Bestimmung hat die
Schwimmerbewegung auf das zu regulirende Organ zu übertragen.
An der inneren Gefäßwand sind 16 gegen den Horizont um 45° geneigte Schaufeln
angegossen und oben durch einen ringförmigen Deckel abgeschlossen.
Die rotirende Bewegung wird dem Apparat mittelst einer am Untertheil des Gefäßes
aufgekeilten Riemscheibe ertheilt.
Pancsova, den 21. Mai 1862.
Tafeln