| Titel: | Experimentelle Untersuchungen über die zum Schmelzen des Roheisens, ferner des Zinns, Bleies, Zinks, der Glockenbronze, des Geschützmetalls und des Messings erforderliche Wärme; von den Ingenieuren Minary und Résal. |
| Fundstelle: | Band 163, Jahrgang 1862, Nr. IX., S. 32 |
| Download: | XML |
IX.
Experimentelle Untersuchungen über die zum
Schmelzen des Roheisens, ferner des Zinns, Bleies, Zinks, der Glockenbronze, des
Geschützmetalls und des Messings erforderliche Wärme; von den Ingenieuren Minary und Résal.
Aus den Annales des
mines, 5me série, 1861, t. XIX p.
401.
Mit einer Abbildung auf Tab. I.
Minary, experimentelle Untersuchungen über die zum Schmelzen des
Roheisens etc. erforderliche Wärme.
Wir haben die zum Schmelzen des Roheisens genau
erforderliche Wärmemenge, das heißt die Gesammtwärme des geschmolzenen Roheisens
bestimmt, um dann den Effect der zum Umschmelzen des Roheisens gebräuchlichen
Apparate (Cupolöfen) und die Verbesserungen deren sie fähig sind, ermitteln zu
können.
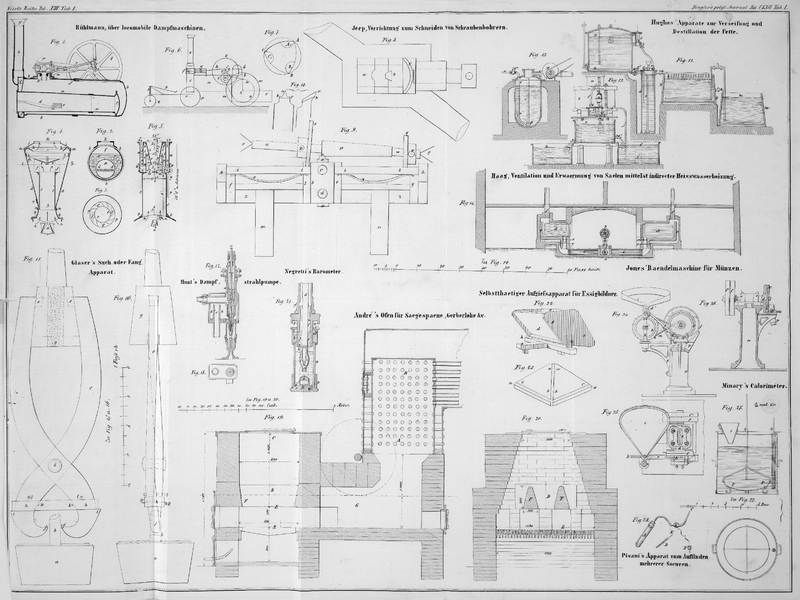
Das von uns angewandte Calorimeter, Fig. 27, besteht aus
einem cylindrischen Gefäß von Eisenblech, welches 4 Decimeter Durchmesser und 4
Decimeter Höhe hat, und mit einem Deckel versehen ist, worin sich drei Oeffnungen
befinden. Die eine derselben, 1, hat 75 Millimeter Durchmesser und dient zum
Einbringen des Roheisens in den Apparat; die zweite, 2, befindet sich in der Mitte,
und durch sie geht die Stange einer concaven Schale, auf welcher sich das Roheisen
absetzt, und die so auf Füßen ruht, daß sie vollkommen mit Wasser umgeben ist; die
dritte Oeffnung, 3, welche sich nahe am Rande des Deckels befindet, correspondirt
mit einer inneren Röhre, die mit Löchern versehen und zur Aufnahme eines
Thermometers bestimmt ist.
Bei unseren Versuchen mit flüssigem Roheisen gossen wir dasselbe in das Calorimeter
mittelst eines auf der großen Oeffnung des Deckels angebrachten Trichters, welcher
vorher mit Asche überzogen worden war, damit nicht ein Theil des Eisens der
Oberfläche anhaften konnte, womit es in Berührung kam.
Das für die Versuche einzuschlagende Verfahren ist leicht zu begreifen; man mißt die
anfängliche Temperatur des Wassers; sobald dann das Roheisen eingebracht ist,
schüttelt man das Wasser, indem man der Schale, welche das Roheisen aufnahm,
mittelst der Stange eine auf und nieder steigende Bewegung ertheilt; man notirt
endlich die Maximaltemperatur, welche das Wasser erlangt. Aus diesen Daten läßt sich
leicht die Gesammtwärme des eingebrachten Roheisens berechnen, indem man die
Wärmecapacität des angewandten Metallgefäßes berücksichtigt.
Der Wärmeverlust durch Strahlung kann vollständig vernachlässigt werden. Wir haben
nämlich durch mehrere Versuche gefunden, daß der durch die Abkühlung per Minute stattfindende Verlust durch die Formel
0,0016 ((T₀ + T)/2 – ϑ)
ausgedrückt werden kann, worin T₀ und T die Maximal- und
Minimaltemperatur des Calorimeters am Anfang und Ende des Versuchs bezeichnen, und
ϑ die umgebende Temperatur.
Da nun die Maximaltemperatur des Wassers stets nach Verlauf von höchstens 2 1/2
Minuten erreicht wurde, so überstieg dieser Verlust bei den Temperaturverhältnissen
unserer Versuche nicht 0°,05 C., während unsere Temperaturzunahmen in der
Regel nicht weniger als 14° betrugen. Uebrigens wird dieser Verlust
mindestens compensirt, wenn man annimmt, wie wir es gethan haben, daß am Ende der
Operation das Calorimeter in seiner ganzen Masse die Endtemperatur des Wassers
erreicht hat, während doch sein oberer Theil und der Deckel natürlich etwas weniger
warm seyn müssen.
Das angewandte Thermometer gestattete uns die Temperaturen auf nahezu 1/10 Grad zu
schätzen.
Um die Fehlerquellen zu vermindern, haben wir in der Regel mit wenigstens 35 Kilogr.
Wasser und 2 Kilogr. Roheisen operirt.
Um die Wägungen leicht vornehmen zu können, wurde das Calorimeter auf eine tragbare
Brückenwaage gestellt, deren Empfindlichkeit sich auf beiläufig 5 Gramme
erstreckte.
Wir haben uns auf das mit Kohks erblasene graue Roheisen aus den Hohöfen von Nans
beschränkt, welches in einem Cupolofen der Maschinenfabrik zu Casamène
(Doubs-Departem.), wo wir unsere Versuche anstellten, umgeschmolzen worden
war.
Nach den Analysen von Minary ist die mittlere
Zusammensetzung dieses Roheisens folgende:
Eisen
0,9450
Silicium
0,0195
Kohlenstoff
0,0309
nicht bestimmte Körper oder Verlust
0,0046
––––––
1,0000.
Wenn das geschmolzene Roheisen in das Wasser des Calorimeters fällt, nimmt es eine
concrescirte Textur mit sehr dünnen Wänden an, welche zahlreiche Höhlungen zeigt; es
kann daher kein Zweifel bleiben, daß die Temperatur in seinen verschiedenen Punkten
am Ende des Versuchs die gleiche ist.
Wir müssen jedoch bemerken, daß das flüssige Roheisen eine theilweise Zersetzung des
Wassers bewirktEine den Eisengießern bekannte Thatsache. Beim Sandguß wird die Feuchtigkeit
des nassen Sandes in Berührung mit dem geschmolzenen Eisen theilweise
zersetzt, und es entwickelt sich daher nebst Wasserdampf auch
Wasserstoffgas, welche beide auf geeignete Weise abgeleitet werden müssen,
damit keine Blasen in dem Gusse entstehen; das aus den Oeffnungen der
Windpfeifen hervordringende Wasserstoffgas wird mittelst eines brennenden
Holzstückes entzündet, und brennt bis nach Beendigung des Gusses von selbst
fort. A. d. Red., welche nur sehr unbedeutend ist, aber dadurch augenfällig wird, daß sich
eine schwache blaue Flamme zeigt, wenn zufällig ein Stückchen rothglühenden Metalls
am Ende des Trichters haftend bleibt.
Wir haben uns durch die Prüfung im Eudiometer überzeugt, daß das entbundene Gas
reiner Wasserstoff ist. Dasselbe wird übrigens in so geringer Menge erzeugt, daß wir
über 10 Kilogr. Roheisen anwenden mußten, um 1 Liter Gas zu erhalten; das Roheisen
zeigt auch nach der Operation keine bemerkbaren Spuren von Oxydation. Man kann
übrigens unter solchen Umständen annehmen, daß die durch die Zersetzung des Wassers
absorbirte Wärme durch die entsprechende Oxydation des Metalls compensirt wird.
Da das Gesammtgewicht des Calorimeters 15,97 Kilogr. beträgt, so ist sein calorisches
Aequivalent an Wasser 1,817 Kilogr., wenn man mit Regnault die specifische Wärme des Schmiedeeisens oder des Eisenblechs zu
0,11379 annimmt. Wir haben ferner die Wärmecapacität des Roheisens nach unserer
Bestimmung zu 0,13 angenommen, um die in demselben nach jeder Operation enthaltene
Wärmemenge berücksichtigen zu können; da diese Correction einem sehr kleinen Bruch
entspricht, so kann man jene Ziffer unbedenklich auf den vorliegenden Fall anwenden,
obgleich sie für eine andere Roheisensorte ermittelt worden ist.
Es bezeichne nun:
T₀ die Anfangstemperatur des Calorimeters;
T die Endtemperatur;
ϑ die umgebende Temperatur;
Q das Gewicht des angewandten Wassers;
q das Gewicht des Roheisens;
A die Gesammtwärme, welche 1 Kilogr. geschmolzenen
Roheisens in seinem anfänglichen Zustande enthält.
Man hat dann die Gleichung
qA – q × 0,13 T = (T – T₀) )Q + 1,817),
woraus folgt
A = 0,13 T + (T – T₀) (Q + 1,817)/q
Als wir Roheisen in eine Gießkelle füllten, und es dann in das Calorimeter in dem
Zeitpunkt gössen, wo sich an der Oberfläche eine feste Kruste zu bilden beginnt,
also nahezu bei dem Uebergang von dem flüssigen in den festen oder teigigen Zustand,
erhielten wir die folgenden Resultate:Wir haben die Werthe von ϑ angegeben,
damit man, wenn es gewünscht wird, die Correction bezüglich der Abkühlung
machen kann.
ϑ
T₀
T
Q
q
A
4°
8°,0
22°,0
36,020
2,100
255,11
3°
20°,0
37°,0
35,030
2,500
255,45
5°
11°,8
26°,8
35,030
2,200
254,71
4°
12°,2
24°,6
35,030
2,000
250,07
4°
11°,8
24°,4
35,030
1,850
254,17
5°
9°,4
23°,5
35,030
2,040
257,72
Die Differenzen welche die Werthe von A zeigen, rühren
daher, daß es trotz aller Vorsicht sehr schwierig ist, nach einander Roheisen von
gleicher Temperatur anzuwenden; dasselbe ist bald etwas heißer, und bald etwas
kälter, weil es vielleicht einige feste Stücke enthält. Man ersieht aber aus der
vorhergehenden Tabelle, daß man die Gesammtwärme des Roheisens in dem Zustande, wo
es gerade noch flüssig ist, als gleich 255 Wärmeeinheiten betrachten kann.
Als wir sehr heißes Roheisen nahmen, und dann allmählich bis zu dem fraglichen
Zustande herabgiengen, erhielten wir die folgenden Resultate:
ϑ
T₀
T
Q
q
A
5°,0
10°,6
25°,8
35,030
1,940
292,040
5°,0
10°,4
30°,4
35,030
2,700
276,85
5°,5
10°,6
44°,0
35,030
4,710
267,01
5°,5
11°,7
38°,4
35,030
3,840
261,19
5°,0
10°,2
26°,8
35,030
2,380
260,48
2°,5
23°,5
45°,0
35,030
3,130
260,09
4°,75
11°,5
33°,0
35,030
3,100
259,24
Nimmt man das Eisen in seinen auf einander folgenden Zuständen von dem Zeitpunkt
angefangen wo es klebrig zu seyn beginnt, so erhält man:
ϑ
T₀
T
Q
q
A
5°
10°,2
25°
35,030
2,280
242,45
3°
10°,8
27°,3
35,030
2,670
230,26
3°
10°,8
22°,2
35,030
1,890
225,14
3°
11°,0
24°,7
35,030
2,270
225,50
Bei den zwei letzteren dieser Versuche hatte das Roheisen die untere Grenze des
teigigen Zustandes erreicht; es wurde aus einer Gießkelle vermittelst eines vorher
erhitzten Spatels genommen.
Bei unseren letzten Versuchen gossen wir das Roheisen vorher in eine prismatische
Sandform; das erhaltene Prisma wurde in Stücke zerbrochen und in das Calorimeter
geworfen. Für Roheisen welches kaum den festen Instand erreichte und wahrscheinlich
noch einige flüssige Theile enthielt, bekamen wir
ϑ
T₀
T
Q
q
A
3°
23°
33°
35,030
1,670
224,93
Eine etwas länger dauernde Abkühlung, wodurch das Roheisen eine so zu sagen körnige
und wenig cohärente Textur erlangte, gab uns
ϑ
T₀
T
Q
q
A
3
11,8
22
35,030
1,770
215,20
Wenn das Roheisen an seiner Oberfläche fest wird und man beseitigt die innere
flüssige Masse, so bleibt ein Skelett zurück, dessen Gesammtwärme 215,20 ist, da die
correspondirenden Elemente sind
ϑ = 3°,
T₀ = 11°,
T = 22°,
Q = 35,030,
q = 1,950
Wenn endlich das Eisen schon ein wenig Consistenz erlangt hat, so findet man A = 204,40 aus den Daten
T₀ = 24°,
T = 37°,
Q = 35,030,
q = 2,400
Da die Gesammtwärme des Roheisens mit den Veränderungen seines physischen Zustandes
beständig variirt, so brauchen wir uns nicht mit seiner latenten Schmelzwärme zu
befassen, wie bei den Körpern, deren Uebergang von dem festen in den flüssigen
Zustand zu rasch erfolgt, als daß man den Zwischenzustand, nämlich den teigigen
Zustand bei verschiedenen Graden, studiren könnte.
Anwendung der erhaltenen Resultate auf das Umschmelzen des
Roheisens in den Cupolöfen.
Die durch die Formen in einen Cupolofen getriebene Luft entwickelt, indem sie 2
Kilogr. Kohlenstoff verbrennt, 8080 Wärmeeinheiten; da dieerzeugten Gase hauptsächlich aus
Kohlensäure bestehen, so werden sie beim Aufsteigen durch die glühende Kohksmasse zu
Kohlenoxyd reducirt, welches in die Esse abzieht. Durch diese zweite chemische
Reaction verschwinden 1637 Wärmeeinheiten; folglich erzeugen 2 Kilogr. Kohlenstoff
nur 8080 – 1637 = 6443 nutzbringende Wärmeeinheiten, also 1 Kilogr. 3221 W.
E.
Bei dem Cupolofen, womit wir experimentirten, werden, abgesehen vom Anheizen, einzig
für den regelmäßigen Betrieb, auf 100 Pfd. producirtes Eisen 10 Pfd. Kohks
aufgewendet; diese Kohks enthalten 12 Proc. Asche, daher 1 Kilogr. dieses
Brennmaterials 0,88 Kohlenstoff entspricht; daraus folgt, daß man, um 1 Kilogr.
Roheisen zu schmelzen, nutzbringend entwickelt
3221/10 × 0,88 = 283,35 Wärmeeinheiten;
diese Ziffer liegt zwischen den Grenzen der aus unseren
Versuchen sich ergebenden Gesammtwärme von 259 und 290 Wärmeeinheiten. Bei einem
mehrstündigen Gießen erreicht jedoch das Roheisen nicht immer den heißen Zustand,
welcher 290 Wärmeeinheiten entspricht.
Aus dem Vorhergehenden ergibt sich auch, daß die Cupolöfen nur 50 Proc. Nutzeffect
liefern.
Die Schlacken unseres Cupolofens haben folgende Zusammensetzung:
Kieselerde
0,318
Thonerde
0,242
Eisenoxydul
0,224
Kalk
0,210
Magnesia
0,006
–––––
1,000
Versuche welche nach dem vorher beschriebenen Verfahren ausgeführt wurden, ergaben
uns im Mittel 336 Wärmeeinheiten für die Gesammtwärme von 1 Kilogr. aus dem
Cupolofen abgelassenen Eisens, wobei jedoch die Wärmemenge bezüglich der
Endtemperatur (welche nicht über 18°,8 betrug) vernachlässigt wurde.
Zwei Versuche mit weißem Roheisen, ebenfalls aus den Hohöfen von Rans, welches in
einem Tiegel im Windofen geschmolzen wurde, ergaben uns für die Gesammtwärme, in dem
Augenblick wo sich an der Oberfläche des Metalls eine Kruste zu bilden anfieng, 246
u. 248 Wärmeeinheiten; diese Ziffern sind niedriger als diejenigen, welche wir für
das graue Roheisen erhielten, bekanntlich ist aber auch das weiße Roheisen
leichtflüssiger. Wir betrachten jedoch diese Resultate als bloße Annäherungen, denn
da das weiße Roheisen eine große Neigung zum Erstarren hat, so würde es die Anwendung eines
noch größeren Kalorimeters erfordern als wir für das graue Roheisen benutzt haben.
Wir beabsichtigen aber später auf diesen Gegenstand zurückzukommen.
Experimentelle Bestimmung der Gesammtwärme einiger anderen
Metalle im flüssigen Zustande.
Wir haben diese Versuche mit demselben Calorimeter und nach dem gleichen Verfahren
wie für das Roheisen angestellt, indem wir die Formel
A = cT +
(T – T₀)/q (1,817 + Q)
anwandten, worin c die specifische
Wärme des Metalls, T₀ die Anfangs- und T die Endtemperatur des Calorimeters, Q das Gewicht des angewandten Wassers, q das Gewicht des angewandten Metalls, A die gesuchte Gesammtwärme bezeichnet.
Kupfer: c;
= 0,09515.
Q
q
T
T₀
A
Zustand des Metalls.
34,030
1,150
13,6
7,8
182,0
Sehr heiß.
34,10034,10034,03034,10034,10034,03034,030
2,0002,3401,5702,3502,7001,8901,370
21,327,116,831,724,621,820,6
11,416,0 9,621,212,613,414,8
180,0173,0166,0163,5162,0161,5154,0
Zwischenzustände
34,030
1,470
24,6
19,0
139,0
Sehr kalt, aber noch flüssig.
Der Uebergang vom flüssigen Zustande in den festen ist beim Kupfer zu rasch, als daß
man den teigigen Zustand erhalten könnte. Der letzte Werth von A scheint der Grenze wo das Metall gerade noch flüssig
ist, gut zu entsprechen, während der erste sich auf die höchste in den Schmelzöfen
erreichbare Temperatur bezieht.
Zinn: c =
0,05695.
Q
q
T
T₀
A
Zustand des Metalls.
34,100„
2,1501,150
13,414,5
10,612,6
47,546,0
Rothglühend
„
1,300
12,0
10,8
34,0
„
1,960
12,6
11,1
28,0
„
1,600
14,3
13,2
26,0
Grenze, wobei das Metall
noch flüssig ist.
Blei: c =
0,0314.
Q
q
T
T₀
A
Zustand des Metalls.
34,100
2,450
12,8
10,2
38,7
Rothglühend.
„
3,020
17,8
15,2
31,5
„
3,800
16,5
14,4
20,4
„
4,430
14,9
12 8
18,2
„
3,110
17,5
16,1
16,7
Grenze, wobei ein anhaltender
flüssiger Zustand zu beobachten
ist.
Zink: c =
0,09555.
Q
q
T
T₀
A
Zustand des Metalls.
34,100
2,170
23,2
17,0
105,0
Rothglühend. Sehr hohe Temperat.
„
2,010
19,6
15,0
84,0
„
2,350
15,0
10,0
78,0
„
3,400
21,4
15,2
67,5
„
2,700
15,4
10,6
63,5
Grenze des anhaltenden
flüssigen Zustandes.
Glockenbronze, welche 20 Proc. Zinn
enthält: c = 0,08751 (berechnet nach der Regel von Person).
Q
q
T
T₀
A
Zustand des Metalls.
34,100
1,870
22,6
14,4
159,5
„
3,150
23,0
11,0
139,0
„
2,930
23,8
13,7
126,0
„
1,200
14,8
11,1
117,0
Geschützmetall, welches 10 Procent
Zinn enthält: c = 0,09133 (berechnet).
Q
q
T
T₀
A
Zustand des Metalls.
34,100
1,570
17,3
8,8
173,0
Sehr hohe Temperatur.
„
1,660
16,7
9,2
164,0
„
2,050
24,0
15,5
151,0
„
4,570
33,0
15,0
144,5
„
2,500
19,6
10,9
127,0
Teigig.
Messing: c
= 0,09527 (berechnet nach einem Gehalt von 30 Proc. Zink).
Q
q
T
T₀
A
Zustand des Metalls.
34,100
3,500
36,2
21,0
159,5
Sehr hohe Temperatur.
„
2,567
22,0
10,8
159,0
Deßgl.
„
3,200
22,6
10,6
137,0
„
1,170
15,0
11,0
124,0
„
1,800
19,0
13,1
119,5
Teigig.
Die drei letzten Tabellen beweisen mit Berücksichtigung der vorhergehenden, daß die
zum Schmelzen einer Legirung erforderliche Maximal- oder
Minimal-Gesammtwärme gleich ist der Summe der analogen Wärmemengen, welche
erforderlich sind, um deren Bestandtheile einzeln zu schmelzen. Man erhält nämlich
folgende Tabelle:
Textabbildung Bd. 163, S. 40
Maximum von A; erhalten; berechnet; Minimum von A;
Geschützmetall; Glockenbronze; Messing;
welche zeigt, daß die Differenzen zwischen den Resultaten des
directen Versuchs und denjenigen wozu man durch Anwendung der vorhergehenden Regel
gelangt, nur sehr gering sind.
Tafeln