| Titel: | Die Meyer'sche variable Expansion als Locomotivsteuerung; von H. Fuhst. |
| Autor: | Hermann Fuhst |
| Fundstelle: | Band 151, Jahrgang 1859, Nr. LXXVIII., S. 321 |
| Download: | XML |
LXXVIII.
Die Meyer'sche
variable Expansion als Locomotivsteuerung; von H. Fuhst.
Mit Abbildungen auf Tab.
V.
Fuhst, über die Meyer'sche variable Expansion als
Locomotivsteuerung.
Im Bulletin de la Société d'Encouragement
von 1849 findet sich bereits die Beschreibung einer mit Meyer's Steuerung versehenen Locomotive. Die Bewegung des
Vertheilungsschiebers wird dabei durch die Stephenson'sche Coulisse vermittelt, deren Functionen hier nur das Umsteuern
und in Ruhe setzen der Maschine sind, weßhalb auch kein anderer als die beiden
äußersten und der todte Punkt derselben zur Benutzung kommt. Ohne weiter auf jene
Beschreibung einzugehen, wollen wir hier nur bemerken, daß diese Steuerung eine
allgemeinere Verbreitung nicht gefunden hat, was wohl hauptsächlich daher gekommen
seyn mag, daß man die Expansionsgränzen derselben überhaupt für beschränkt hielt,
und dann allerdings, da die Anwendung des zweiten Schiebers die Summe der zu
überwindenden Widerstände nicht unbeträchtlich erhöht, große Vortheile von ihr nicht
erwarten durfte.
Hr. Professor Zeuner in Zürich hat bereits nachgewiesen,
daß die Expansionsgränzen dieser Steuerung in Wirklichkeit gar nicht so beschränkt
sind, als man früher glaubte, daß vielmehr ihre Leistung, namentlich in Betreff der
variablen Expansion, bei richtiger Bestimmung der einzelnen Dimensionen nichts zu
wünschen übrig läßt. Derselbe kommt am Schlusse seiner Entwickelungen (siehe: die
Schiebersteuerungen, mit besonderer Berücksichtigung der Steuerungen bei
Locomotiven, Freiberg 1858) zu dem Resultate, daß eine im Sinne der von ihm
aufgestellten Theorie construirte Meyer'sche Steuerung,
bei Bewegung des Hauptschiebers durch eine Stephenson'sche Coulisse, für den Vorwärtsgang der Locomotive jeden
Expansionsgrad zuläßt, während die Gränzen der Expansion für den Rückwärtsgang bei 0
und 3/4 des Hubes liegen.
Diese Resultate sind gewiß anerkennenswerth, und denen, die derselbe Autor in dem
bereits angezogenen Werke für die ebenfalls mit zwei Schiebern arbeitende Steuerung
von Gonzenbach findet, weit überlegen; jedoch lassen sich
dieselben in Betreff des Rückwärtsganges und in Bezug auf die Größe der auf Reibung
wirkenden Fläche des Vertheilungsschiebers noch erweitern.
Indem nämlich nach der Theorie von Zeuner der
Voreilungswinkel des Expansionsexcenters kleiner ist als 90°, fällt für den
Rückwärtsgang das Maximum der relativen Schieberentfernung größer aus, als für den
Vorwärtsgang. Um nun beim Rückwärtsgange die dem Beginn des Hubes nahe gelegenen
Expansionsgrade erreichen zu können, ist es nothwendig die Länge der
Expansionsschieberplatten sowohl, als auch die Entfernung von Außenkante zu
Außenkante der Dampfdurchlaßcanäle im Hauptschieber, auf der der
Schieberkastenfläche abgekehrten Seite desselben, nach den Bewegungsverhältnissen
der Schieber für den Rücklauf der Locomotive zu bestimmen, wodurch die erwähnten
beiden Maaße, welche Factoren der zu überwindenden Reibungswiderstände sind, größer
ausfallen als für den Vorwärtsgang nöthig ist, und außerdem getrennte
Expansionsscalen für Vor- und Rückwärtsgang erforderlich werden.
Um dieses zu umgehen, habe ich in Nachstehendem eine Construction aufgestellt, welche
für Vor- und Rückwärtsgang der Maschine gleiche Bewegungsverhältnisse der
Schieber ergibt und somit nur eine Expansionsscala
erfordert. Zugleich habe ich, da das Arretiren der Maschine durch den
Expansionsschieber möglich ist, die Benutzung des todten Punktes der Stephenson'schen Coulisse also umgangen werden kann,
statt dieser eine gerade um ihren todten Punkt sich drehende Coulisse, welche nur
durch ein Excenter bewegt zu werden braucht, in Anwendung gebracht. Diese
Construction macht es unmöglich, dem Vertheilungsexcenter einen Voreilungswinkel zu
geben, nichtsdestoweniger können wir auf eine äußerst einfache, der Meyer'schen Steuerung eigenthümliche Weise, ein auf
beiden Seiten gleiches, bei allen Expansionsgraden für Vor- und Rückwärtsgang
constantes Voreilen des Vertheilungsschiebers, und außerdem die möglichst kleinste
Größe der auf Reibung wirkenden Fläche desselben erlangen.
Beschreibung der Steuerung.
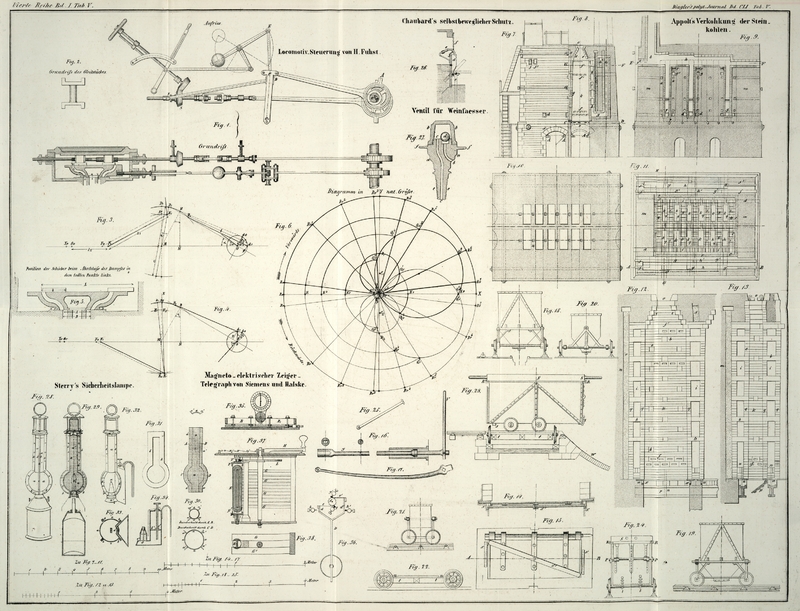
Es ist A, Fig. 1, das Excenter des
Vertheilungsschiebers, welches, unveränderlich fest auf der Radwelle sitzend,
vermittelst seiner Stange die Bewegung der um M sich
drehenden Coulisse C, C₁ bewirkt. Das Gleitstück
D kann durch die Stange E,
D in Folge der daran befestigten Hebelcombination gehoben und gesenkt
werden, und veranlaßt seinerseits wieder durch die Stange F,
D die Bewegung des Vertheilungsschiebers. Das hintere Excenter ist das des
Expansionsschiebers; die Stange desselben greift direct an die Expansionsschieberstange, auf welcher
sich zum Verstellen der Expansion resp. zum in Ruhe setzen der Maschine das conische
Rädchen S befindet. Der hierher gehörige Mechanismus ist
derselbe, wie wir ihn bei Anwendung der Meyer'schen
Steuerung auf stationäre Maschinen in wechselnder Bewegungsrichtung im
vorhergehenden Hefte dieses Journals speciell gezeichnet und erörtert haben, weßhalb
wir ihn als bekannt voraussetzen.
Die Wirkung der Stange E, D ist eine doppelte. Einmal
nämlich soll sie das Heben oder Lenken des Gleitstückes ermöglichen, dann aber auch
soll sie eine möglichst horizontale Bewegung desselben veranlassen, weßhalb der von
ihrem oscillirenden Ende beschriebene Bogen flach, sie selbst somit, diesem
entsprechend, lang seyn muß. Der Punkt B, in welchem die
Stange des Vertheilungsexcenters mit der Coulisse verbunden ist, ist so gewählt, daß
wenn die Coulisse in verticaler Richtung steht, eine von dem Mittelpunkt O der Radwelle auf die Linie MB gefällte Normale die Höhe des von B beschriebenen Bogens halbirt.
Theorie der Steuerung.
Für die jetzt aufzusuchende Relation zwischen beliebigen Drehungswinkeln der Kurbel
und der ihnen jedesmal entsprechenden Entfernung des Schiebers von seiner mittleren
Stellung, gehen wir davon aus, daß, wenn der Schieber und das Excenter in ihrer
mittleren Stellung angekommen sind, die Coulisse vertical steht; denn nur für diesen
Fall bleibt, wie man aus den folgenden Entwickelungen leicht ableiten kann, der
Schwingungsmittelpunkt des Schiebers beim Vor- und Rückwärtsgange der
Maschine unverrückt an seiner Stelle. Denken wir nun beim Vorwärtsgange der
Maschine, ohne auf die Stellung der Kurbel Rücksicht zu nehmen, das Excenter des
Vertheilungsschiebers in seiner mittleren Stellung Od₀ (Fig. 3) angekommen, so sind wir zunächst im Stande die Entfernung OX vom Schwingungsmittelpunkte des Schiebers bis zum
Mittelpunkte der Radwelle festzustellen.
Der Steuerungsmechanismus nimmt alsdann die in Fig. 3 oberhalb der
Horizontalen OX mit punktirten Linien angegebene
Stellung ein und es ist:
Textabbildung Bd. 151, S. 323
Führen wir in diese Formel die in der Figur für die einzelnen
Werthe eingeschriebenen Bezeichnungen ein, so entsteht:
Textabbildung Bd. 151, S. 324
oder
OX = l₂ +
√(l₁² – c²) + C sin α
+ √(l² – r² – C²cos²α)
(Gleichung 1).
Ehe wir zur Bestimmung des Schieberweges selbst übergehen, wollen wir das Gesetz
aufsuchen, nach welchem die Oscillation des Punktes B
erfolgt, und dabei annehmen, daß alle die verschiedenen Stellungen, welche dieser
Punkt während seiner Oscillation einnimmt, mit derjenigen Linie zusammenfallen,
welche von dem Mittelpunkte O der Radwelle aus durch den
Halbirungspunkt der Höhe des von B beschriebenen Bogens
gedacht werden kann. Diese Annahme rechtfertigt sich durch die oben angegebene
Construction des Punktes B in Bezug auf den Punkt O.
Nehmen wir für unsere Rechnung den Voreilungswinkel des Vertheilungsexcenters gleich
δ an, und lassen nun die Kurbel aus dem
todten Punkte links um den Winkel ω heraustreten,
so ist in Folge dessen die Excentricität in die Richtung Od₁ gekommen, und es ist der Punkt B um
BB₁ von seiner mittleren Stellung
abgerückt.
Die Figur ergibt nun:
BB₁ = OB – OB₁,
Textabbildung Bd. 151, S. 324
und
Textabbildung Bd. 151, S. 324
Bilden wir jetzt BB₁, so ergibt sich:
BB₁ = r sin (ω + δ)
– r²sin²(ω + δ)/2l.
Setzen wir für ω : ω + 180°, so ist
BB₁ = – r sin
(ω + δ) +
r²sin²(ω + δ)/2l;
d.h. die Oscillation des Punktes B
erfolgt symmetrisch zu beiden Seiten seiner mittleren Stellung.
Den Ausdruck r²sin²(ω + δ)/2l dürfen wir in den obigen beiden
Gleichungen vernachlässigen, wenn l gegen r sehr groß ist; in dem Falle jedoch, daß der nominelle
Werth des in Rede stehenden Quotienten sich so groß herausstellt, daß eine
Vernachlässigung desselben zu bemerkbaren Ungenauigkeiten im Diagramme führen würde,
steht uns zur Ausgleichung derselben die im polytechn. Journal Bd. CL S. 242 gegebene Hülfsconstruction zu
Gebote, so daß wir auch in diesem Falle setzen dürfen:
BB₁ = r sin (ω + δ),
oder allgemein:
BB₁ = ± r sin
(ω + δ)
(Gleichung 2).
Jetzt können wir nun auch zur Berechnung des Schieberweges selbst, d.h. zur
Entfernung des Schiebers von seiner mittleren Stellung, nachdem die Kurbel den
Winkel ω durchlaufen hat, übergehen. Nachdem
diese Drehung erfolgt ist, nimmt der Steuerungsmechanismus die in ausgezogenen
Linien oberhalb der Horizontalen OX angegebene Stellung
ein. Da in Folge der Länge der Stange E, D (Figur 1) der
von ihrem oscillirenden Ende beschriebene Bogen sehr flach ist, so können wir die
normalen Entfernungen der einzelnen Punkte dieses Bogens von der Horizontalen OXv (Figur 3) gleich der halben
Coulissenlänge c annehmen, zumal wenn wir die Stange so
aufhängen, daß der Halbirungspunkt der Höhe des von ihrem unteren Ende beschriebenen
Bogens mit dem höchsten Punkte des von der halben Coulissenlänge beschriebenen
Bogens zusammenfällt.
Nennen wir jetzt für den Vorwärtsgang den dem Drehungswinkel ω entsprechenden Schieberweg ξv,
so ergibt sich mit Berücksichtigung des Obigen:
ξv = OXv – OGv;
OX ist aus Gleichung 1 bekannt, für OG erhalten wir:
Textabbildung Bd. 151, S. 325
Da nun: Winkel MBH = Winkel D₀MB = Winkel α und nach Gleichung 2:
ON = r sin (ω + δ) = BB₁
ist, so geht die obige Gleichung, wenn wir außerdem noch die
bekannten Bezeichnungen einführen, über in:
Textabbildung Bd. 151, S. 325
Da nun:
BO = √(l²
– r²)
so ist schließlich:
OG = l₂ +
√(l₁² – c²) – E₀E₁ + C
sin α + √(l² – r² – C²cos²α).
Ziehen wir diese Gleichung von Gleichung 1 ab, so erhalten wir:
ξv = E₀E₁.
Es verhält sich nun:
E₀E₁
: D₀D₁
= E₀M : D₀M,
E₀E₁
: BB₁
= E₀M : D₀M,
oder:
ξv : ± r sin
(ω + δ) =
c : C,
mithin ist:
ξv = ± c/C r sin (ω + δ) (Gleichung 3);
dabei gilt das obere Vorzeichen für die Bewegung des Kolbens
von Links nach Rechts, das untere für die von Rechts nach Links.
Wir ersehen aus Gleichung 3, daß die symmetrische Bewegung des Punktes B zu beiden Seiten seiner mittleren Stellung, sich nach
Maaßgabe des Verhältnisses c/C auf die Bewegung des Schiebers um seine mittlere Stellung überträgt.
Rückwärtsgang der Maschine.
Der Rückwärtsgang wird dadurch hergestellt, daß man das Gleitstück, welches sich beim
Vorwärtsgange um die halbe Länge der Coulisse über dem Drehpunkte derselben
befindet, so weit senkt, daß es sich um ebensoviel unterhalb desselben befindet.
Dabei ist die Aufhängung der Stange EK₁ (Fig. 4), durch
welche die Verschiebung des Gleitstückes erfolgt, auch für den Rückwärtsgang der Art
zu bewerkstelligen, daß der Halbirungspunkt der Höhe des von ihrem oscillirenden
Ende beschriebenen Bogens mit dem höchsten Punkte des von der halben Coulissenlänge
beschriebenen Bogens zusammenfällt.
Denken wir zunächst wieder, ohne Rücksicht auf die Stellung der Kurbel, das Excenter
in seiner mittleren Stellung angekommen, so steht die Coulisse wieder vertical, und
wir erhalten für die Entfernung OX
Fig. 4:
Textabbildung Bd. 151, S. 326
oder bei Einführung der in Figur 3 eingeschriebenen
Bezeichnungen:
OXr = l₂ +
√(l₁² – c²) + C sin α
+ √(l² – r² – C²cos²α).
Die rechte Seite dieser Gleichung ist identisch mit der
rechten Seite der Gleichung 1, mithin ist:
OXv = OXr,
d.h. die Entfernung des Schwingungsmittelpunktes des Schiebers
vom Mittelpunkte der Radwelle ist für Vor- und Rückwärtsgang der Maschine
dieselbe.
Wir bestimmen nun erst wieder das Gesetz, nach welchem die Oscillation des Punktes
B erfolgt. Dasselbe ergibt sich unter Beibehaltung
der für den Vorwärtsgang gemachten Annahmen:
BB₁ = OB₁
– OB,
Textabbildung Bd. 151, S. 327
OB = l² – r²/2l (nach
Oben);
mithin:
BB₁ = r sin (ω – δ)
+ r²sin²(ω – δ)/2l.
Setzen wir für ω : ω + 180°, so entsteht:
BB₁ = – r sin
(ω – δ) – r²sin²(ω
– δ)/2l.
Aus diesen beiden Gleichungen folgt zunächst, daß die Bewegung des Punktes B auch hier symmetrisch zu beiden Seiten seiner
mittleren Stellung erfolgt, während wir zugleich aus denselben ersehen, daß das
Gesetz der Oscillation dieses Punktes beim Rückwärtsgange ein anderes ist als beim
Vorwärtsgange.
Lassen wir auch hier das Glied r²sin²(ω
– δ)/2l
bestimmen nun den dem Drehungswinkel ω
entsprechenden Schieberweg ξr, so ist
zunächst:
ξr + OXr – OGr;
OXr ist bekannt, für OGr
ergibt sich:
Textabbildung Bd. 151, S. 328
Da nun:
Winkel MBH = Winkel D₀MB = Winkel α
und
ON = r sin (ω – δ)
= BB₁,
so folgt mit Einführung der bekannten Bezeichnungen:
Textabbildung Bd. 151, S. 328
mithin:
OGr = l₂√(l₁² – c²) – K₀K₁ + C sin α +
√(l² – r² – C²cos²α).
Bilden wir jetzt, indem wir diese Gleichung von der für OXr erhaltenen abziehen, ξr, so
entsteht:
ξr = K₀K₁.
Es verhält sich nun wieder:
K₀K₁ : D₀D₁ = K₀M :
D₀M,
K₀K₁ : B₁B₁ = K₀M
: D₀M,
oder:
ξr : r sin (ω – δ)
= c : C;
mithin ist:
ξr = c/C r sin (ω –
δ).
Wenn wir für ω setzen ω + 180°, so erhalten wir:
ξr = – c/C r sin (ω + δ).
Stellen wir jetzt die verschiedenen, durch die obige Rechnung erhaltenen Resultate
zusammen, so kommen wir zu dem Schlusse:
„Die Oscillation des Vertheilungsschiebers geschieht beim Vor- und
Rückwärtsgange der Maschine symmetrisch zu beiden Seiten eines Punktes, dessen
Entfernung vom Mittelpunkte O der Radwelle sich
ausdrückt durch:
l₂ + √(l₁² – c²) + C sin α + √(l² – r² – C²cos²α),
während das Gesetz der Oscillation für den Vorwärtsgang enthalten ist in:
ξv = ± r
sin (ω + δ)
und das für den Rückwärtsgang in:
ξv = ± r
sin (ω – δ) (Gleichung 4),
wobei das positive Vorzeichen stets für die Bewegung des Kolbens von Links nach
Rechts und das negative für die von Rechts nach Links gilt.“
Bei der Annahme: δ > 0 würden wir für die in Rede
stehende Steuerung beim Vorwärtsgange eine sehr
zweckmäßige Dampfvertheilung mit constantem positiven
Voreilen für jeden Expansionsgrad erhalten, während wir beim Rückwärtsgange ein zwar ebenfalls für alle
Expansionsgrade constantes aber negatives Voreilen
erzielen würden, wovon man sich leicht durch Aufzeichnen des entsprechenden
Diagrammes überzeugen kann. Die Folgen eines negativen
Voreilens sind stets die Eröffnung des
Dampfeintrittscanales nach Beginn des Hubes, weßhalb eine Steuerung die
dieses Uebel besitzt, auch wenn es nur beim Rücklauf der Maschine der Fall ist,
immer als unbrauchbar verworfen werden muß, woraus für uns die Nothwendigkeit folgt:
δ = 0 zu nehmen.
Bei Maschinen die mit großer Geschwindigkeit arbeiten, wie bei den Locomotiven dieß
der Fall ist, wird ein lineares Voreilen von einigen Millimetern als sehr
vortheilhaft auf die effective Leistung einwirkend angesehen. Sobald Steuerungen nur
mit einem Schieber arbeiten, gleichviel ob dieselben auf fixe oder variable
Expansion berechnet sind, ist ein lineares Voreilen nur dann möglich, wenn δ > 0; bei den Meyer'schen Steuerungen hingegen ist in Folge der eigenthümlichen Form des
Vertheilungsschiebers und der wechselseitigen Wirkung des Vertheilungs- und
des Expansionsschiebers ein lineares Voreilen auch bei der Annahme δ = 0 herzustellen. Macht man nämlich, wie Fig. 5 es
zeigt, die Entfernung A der inneren Kanten der
Dampfdurchlaßcanäle im Hauptschieber kleiner als die Entfernung B der äußeren Kanten der Dampfdurchlaßcanäle im
Cylinder, und sorgt dafür, daß wenn auf der einen Seite der Dampfabschluß erfolgt
ist, die Wiedereröffnung des Dampfeintrittscanales im Vertheilungsschieber auf
derselben Seite erst dann eintritt, wenn der Dampfdurchlaßcanal im Cylinder durch
den Vertheilungsschieber selbst bereits abgesperrt ist, was, wie sofort einleuchten
wird, erst nach erfolgtem Hubwechsel stattfinden kann, so erhält man ein lineares
Voreilen, dessen nomineller Werth v sich ausdrückt
durch:
v = (B – A)/2.
Auf welche Weise es zu erlangen ist, daß der Dampfeintrittscanal im
Vertheilungsschieber nach erfolgter Schließung durch den Expansionsschieber sich
erst wieder öffnet, nachdem der erstere den Dampfdurchlaßcanal im Cylinder bereits
abgesperrt hat, wird aus Betrachtung des Diagrammes Fig. 6 hervorgehen.
Diagramm der Steuerung.
Die Betrachtung des Diagrammes möge in Gestalt der folgenden Construction
geschehen:
Es ist eine Locomotive mit Meyer's variabler Expansion so
anzuordnen, daß bei der Breite der Dampfcanäle im Cylinder a = 0m,126, und dem linearen
Voreilen des Vertheilungsschiebers v = 0m,003 alle Expansionsgrade für Vor-
und Rückwärtsgang der Maschine von 0 bis 0,8 des Hubes erreichbar sind.
Wie groß sind die Radien des Vertheilungs- und Expansionsexcenters?
Welches sind die Längen der Expansionsschieberplatten, und wie lang ist der
Vertheilungsschieber von Außenkante zu Außenkante der Dampfdurchlaßcanäle auf der
der Schieberkastenfläche abgelehrten Seite gemessen?
Um wie viel sind die Expansionsschieberplatten jedesmal aus einander zu schieben, um
die Expansionsgrade 0, 1/6, 2/6, 3/6, 4/6 und die obere Expansionsgränze zu
erreichen?
Auflösung. Setzen wir in Gleichung 3 und 4 δ = 0, so erhalten wir allgemein:
ξ = ± c/C r sin ω (Gleichung 5),
wobei das positive Vorzeichen für die Bewegung des Kolbens von
Links nach Rechts, das negative für die von Rechts nach Links gilt, gleichviel, ob
die Locomotive sich im Vor- oder Rücklaufe befindet.
Nehmen wir jetzt an, daß für den größten Schieberweg ξg, d.h. für die weiteste Entfernung des Schiebers von seiner
mittleren Stellung, deren Eintritt erfolgt, wenn der Schieber sich in einem seiner
todten Punkte befindet, der als Dampfeintrittscanal fungirende Durchlaßcanal im
Cylinder um die Größe des äußeren Voreilens v
überöffnet ist, so ergibt sich:
ξg = v + a – v = a.
Für ξg ist w = 1R und somit sinω = 1;
mithin ist:
ξg = ± c/C r,
oder:
a = ± c/C r,
folglich:
r = ± C/c a,
oder in absoluter Hinsicht:
r = C/c a.
Die vorstehende Gleichung ergibt den Werth des Radius vom Vertheilungsexcenter,
welcher hier jedoch nicht gleichbedeutend mit demjenigen des Durchmessers vom
Hauptschieberkreise ist. Der letztere ist natürlich gleich ξg und ξg ist nach Oben gleich
a.
Sind nun in Fig.
6
OX und OY die
Coordinatenachsen des Diagrammes, so erhalten wir die Bewegungskreise des
Hauptschiebers, wenn wir aus C₁ und C₂ mit C₁O und C₂O gleich a/2 als Radius die
Kreise OD₁ und OD₂ schlagen. Die Größe des Radius vom Expansionsexcenter, dessen
Voreilungswinkel wir gleich 90° annehmen, finden wir auf folgende Weise. Man
zeichnet zuerst die Kurbelstellung, welche der oberen Expansionsgränze entspricht;
Fig. 6 ist
ORv⁵ für Vorwärtsgang und ORr⁵ für den Rückwärtsgang der Maschine im
Hingange des Kolbens die entsprechende Kurbelstellung. (Bei sämmtlichen in der Figur
verzeichneten Kurbelstellungen ist zwischen Kurbel und Bleuelstange das Verhältniß 1
: 5 angenommen.) Ferner beschreibt man aus O mit dem
linearen Voreilen
Ov = v = (B – A)/2
als Radius einen Kreis, und sucht nun zunächst diejenige
Kurbelstellung auf, bei welcher der als Dampfeintrittscanal fungirende Durchlaßcanal
im Cylinder durch den Hauptschieber selbst geschlossen wird. Die Eröffnung des
Dampfeintrittscanales im Cylinder ist stets gleich ξ + v; dieses in Betracht ziehend, wird
man sofort erkennen, daß Rr⁷ die gesuchte
Kurbelstellung für den Vorwärtsgang ist. Es ist nämlich bei ihr ξ negativ und in absoluter Hinsicht gleich v, weßhalb sich für die Eröffnung des
Dampfeintrittscanales bei dieser Kurbelstellung – v + v = 0 ergibt. Wir sehen hier, daß, wie
Oben bereits angedeutet wurde, die Schließung des Dampfeintrittscanales erst nach
erfolgtem Hubwechsel stattfindet. Aus den in den vorhergehenden Heften dieses Bandes
erschienenen Untersuchungen über die Meyer'sche Steuerung
geht allgemein hervor, daß nach erfolgter Expansion ein nochmaliger Eintritt des
Dampfes nicht stattfinden kann, wenn die relative Schieberentfernung bei der der
oberen Expansionsgränze entsprechenden Kurbelstellung gleich der relativen
Schieberentfernung bei derjenigen Kurbelstellung ist, bei welcher der
Vertheilungsschieber den Dampfeintrittscanal im Cylinder abschließt. Diese
Kurbelstellungen sind, wie wir oben fanden, ORv⁵
und ORr⁷, und wir erhalten gleiche relative
Schieberentfernungen für sie, wenn der Durchmesser des die relativen
Schieberentfernungen angebenden Kreises in die Halbirungslinie des von ihnen
gebildeten Winkels fällt.
Halbiren wir demnach Winkel Rv⁵ORr⁷, ziehen durch D₁ eine Parallele mit OX und durch den
hierdurch bestimmten Punkt Qv⁶ eine Parallele mit
OD₁, so ist Qv⁶O der Durchmesser des
Hülfsschieberkreises in Bezug auf Richtung und Größe, und OE₀ ist die Größe des Radius vom Expansionsexcenter bei dem
Voreilungswinkel 90°.
Das Diagramm läßt nun sofort ersehen, daß sich dieselben Resultate für den Hergang
des Kolbens beim Vorwärtsgang der Maschine, sowie für den Hin- und Hergang
desselben beim Rücklaufe der Locomotive für diese beiden Größen ergeben werden,
woraus weiter folgt, daß auch für alle diese Fälle gleichlautende Resultate für die
Länge l der Expansionsschieberplatten, für die Länge L des Vertheilungsschiebers, sowie für die einzelnen
Größen, um welche die Expansionsschieberplatten aus einander geschoben werden
müssen, um den Eintritt der Expansion bei den vorgeschriebenen Kolben- resp.
Kurbelstellungen zu ermöglichen, entstehen müssen.
Im Diagramme Fig.
6 finden wir die Construction des Durchmessers vom Hülfsschieberkreise und
die daraus sich ergebende Größe des Radius vom Expansionsexcenter nicht für alle
diese Fälle, sondern nur noch, um der Uebersichtlichkeit des Diagrammes keinen
Abbruch zu thun, für den Hingang des Kolbens beim Rücklaufe der Maschine
ausgeführt.
Aus den vorstehend angezogenen Untersuchungen ergibt sich nun die Länge l der Expansionsschieberplatten:
l = OE₀ + OQv⁶ + a,
l = 0m,138
und die Länge L des
Vertheilungsschiebers:
L = 2 l + OE₀ + OQv⁵,
L = 0m,579.
Durch diese Resultate entsteht die in Fig. 5 gezeichnete Form
des Vertheilungsschiebers, aus welcher man sofort ersieht, daß das Maaß ab der auf Reibung wirkenden Fläche desselben auf
die kleinste mögliche Größe zurückgeführt ist. In allen Fällen, bei welchen man das
lineare Voreilen des Vertheilungsschiebers dadurch erzielt, daß man dem Excenter
desselben einen Voreilungswinkel größer als Null gibt, muß dieß Maaß der auf Reibung
wirkenden Fläche größer ausfallen, als dieß hier der Fall ist.
Damit nun auf ein und derselben Seite des Kolbens nicht Ein- und Austritt des
Dampfes zugleich stattfinden können, muß dem Schieber eine innere Ueberdeckung von
der Größe des äußeren Voreilens gegeben werden. Schlagen wir Fig. 6 aus O mit der inneren Ueberdeckung einen Kreis, so fällt
derselbe mit dem schon vorhandenen des äußeren Voreilens zusammen, so daß sich folgende Resultate
für die Dampfvertheilung ergeben. Im todten Punkte links hat der Hauptschieber den
Dampfdurchlaßcanal im Cylinder um die Größe des äußeren Voreilens geöffnet, während
der Dampfaustritt rechts verschlossen ist. Bei der Kurbelstellung ORv, bei welcher der Vertheilungsschieber einen Weg
gleich dem äußeren Voreilen resp. der inneren Ueberdeckung zurückgelegt hat, ist die
Eröffnung des Dampfeintrittscanales gleich 2v, während
die des Dampfaustrittes gleich Null ist; bei dieser Kurbelstellung beginnt somit der
Dampfaustritt rechts und wir erhalten eine Compression des verbrauchten Dampfes,
während die Kurbel den Bogen R₀Rv durchläuft. Der Hub, welchen der Kolben während
dieses Drehungsbogens der Kurbel macht, ist so unbeträchtlich, daß wir ihn gleich
Null setzen können. Nachdem nun bei irgend einer Kolbenstellung Expansion
eingetreten ist, öffnet sich bei der Kurbelrichtung ORv⁷ der Dampfeintritt rechts, während gleichzeitig bei derselben
Kurbelstellung der Dampfaustritt auf derselben Seite geschlossen wird, wodurch jede
Compression des verbrauchten Dampfes vermieden ist.
Obgleich der Arbeitsverlust, welcher bei den gewöhnlichen Locomotivsteuerungen auf
der einen Seite durch Compression entsteht, durch die Arbeit, welche dieser
comprimirte Dampf nach erfolgtem Hubwechsel wieder producirt, zum Theil aufgehoben
wird, so kann doch dieser letzte Arbeitsgewinn den obigen Arbeitsverlust nie ganz
aufwiegen, weßhalb es als ein Vortheil dieser Steuerung angesehen werden dürfte, daß
durch sie die Compression des verbrauchten Dampfes umgangen wird.
Sind die Expansionsschieberplatten ganz zusammengezogen, so tritt unserer
Construction gemäß die Expansion bei 0,8 des Hubes ein. Man findet nun die Größen,
um welche dieselben aus einander geschoben werden müssen, um die übrigen
Expansionsgrade zu erreichen, direct aus den Differenzen der betreffenden relativen
Schieberentfernungen, welche der besseren Uebersichtlichkeit wegen sämmtlich auf der
Horizontalen RvX zusammengetragen worden sind.
Es muß hiernach jede Expansionsschieberplatte zur Erreichung:
der Expansion nach 0
des Hubes um
EE₀ = 0m,103,
„ „
„ 1/6
„ „
„
EE₁ = 0m,070,
„ „
„ 2/6
„ „
„
EE₂ = 0m,046,
„ „
„ 3/6
„ „
„
EE₃ = 0m,0285,
„ „
„ 4/6
„ „
„
EE₄ = 0m,011,
„ „
„ 0,8
„ „
„
EE = 0m,000
nach Außen verschoben werden.
Das Diagramm für den Rückwärtsgang gibt, wie Fig. 6 zeigt, ganz
dieselbe Expansionsscala wie für den Vorwärtsgang, so daß die Ausführung nur eine Scala erfordert.
Stellen wir schließlich die Resultate dieser Anordnung zusammen und vergleichen
dieselben mit jenen Steuerungen, bei denen der Vertheilungsschieber durch die Stephenson'sche Coulisse bewegt wird und der
Voreilungswinkel des Expansionsexcenters kleiner ist als 90°, so können wir
zunächst in Bezug auf die Herstellungskosten den Vortheil, der uns durch Anwendung
einer geraden, nur durch ein Excenter bewegten Coulisse erwächst, bezeichnen,
während wir in constructiver Hinsicht Erreichung aller Expansionsgrade für
Vor- und Rückwärtsgang der Locomotive, Vermeidung der Compression des
verbrauchten Dampfes und Erreichung der möglich kleinsten auf Reibung wirkenden
Fläche des Vertheilungsschiebers haben.
Rechnet man hierzu noch ein unter allen Bedingungen constantes Voreilen des
Vertheilungsschiebers, welches der Meyer'schen Steuerung
an und für sich eigen ist, so dürften diese Resultate wohl ausreichend seyn, das Plus der Reibungswiderstände, welches die Anwendung von
zwei Schiebern gegenüber den Steuerungen mit einem Schieber erzeugt,
aufzuwiegen.
Die hier in Anwendung gekommene Methode, das lineare Voreilen des
Vertheilungsschiebers und die damit verbundene kleinste auf Reibung wirkende Fläche
desselben zu erhalten, läßt sich, da sie unabhängig vom Umsteuerungsmechanismus ist,
auch bei den im vorhergehenden Hefte dieses Journals zur Besprechung gekommenen
stationären Maschinen mit wechselnder Bewegungsrichtung mit Vortheil anbringen.
Tafeln