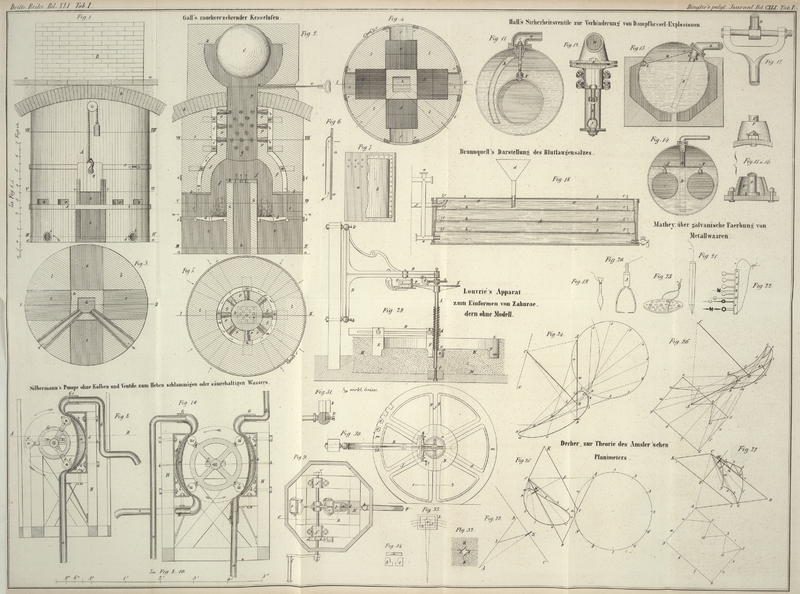
| Titel: | Zur Theorie des Amsler'schen Planimeters; von Professor G. Decher. |
| Autor: | Georg Decher [GND] |
| Fundstelle: | Band 141, Jahrgang 1856, Nr. V., S. 29 |
| Download: | XML |
V.
Zur Theorie des Amsler'schen Planimeters; von Professor G. Decher.
Mit Abbildungen auf Tab.
I.
Decher, zur Theorie des Amsler'schen Planimeters.
In einem Aufsatze: „Ueber das Polar-Planimeter“ S.
321–327 des vorhergehenden Bandes dieses Journals sucht Hr. Amsler sein patentirtes Instrument zu empfehlen und gegen
die Ausstellungen, welche ich gegen das Princip desselben erhoben habe, zu
vertheidigen, was ich sehr natürlich finde; und wenn sich Hr. Amsler begnügt
hätte, darauf hinzuweisen, daß durch die Erfahrung eine für viele praktische Zwecke
hinreichende Genauigkeit des Instrumentes nachgewiesen werde, so hätte ich ihm gerne
stillschweigend zugegeben, daß ich, zuviel Gewicht auf den theoretischen
Gesichtspunkt und die Möglichkeit einer fehlerhaften
Angabe legend, die Wahrscheinlichkeit derselben außer
Berechnung gelassen habe, und daß, von dem genügsamen Standpunkte des Hrn. Amsler angesehen, das Instrument bei seiner Wohlfeilheit
recht gute Dienste leisten könne. Auch werde ich gar nichts dagegen einwenden, wenn
irgend Jemand die Amsler'sche Begründung der Theorie des
Instrumentes streng und bündig genug findet. Wenn aber Hr. Amsler in seinem Eifer soweit geht, meinen Beweis dieser Theorie für unrichtig zu erklären und mir unklare Vorstellungen
vorzuwerfen, so kann ich nicht umhin, ihn darin zurechtzuweisen.
Der Drehungswinkel φ des Rädchens ist eine
Function der beiden unabhängigen Veränderlichen r und
ω' (wie Hr. Amsler
den Winkel XCD, Fig. 24, bezeichnet hat),
da sich φ mit r
allein oder mit ω' oder mit beiden zugleich
ändern kann; es wird daher dφ/dω' so abgeleitet, als wenn r unveränderlich wäre, und bleibt derselbe Ausdruck, ob
r veränderlich oder unveränderlich genommmen wird;
ist also dφ/dω' = dφ/dω für ein constantes r, so besteht
diese Gleichung auch für ein veränderliches r. Es
scheint sich Hr. Amsler nicht viel über den in der Praxis
gangbaren hausbackenen Begriff von den Differentialen erhoben zu haben, mit dem man
eben bei Functionen mit mehreren Veränderlichen nicht ganz ausreicht. Wenn übrigens
der vorstehende Beweis Hrn. Amsler nicht gründlich und
bündig genug dünkt, so mag er sich von seiner Fläche-Elementen-Theorie
sagen lassen, daß man jede ebene Figur, welche von zwei sich schneidenden Geraden
und einer Curve begränzt wird, als die Summe von sehr spitzen Kreissectoren
betrachten kann; für jeden einzelnen Sector hat man aber als entsprechenden
Drehungswinkel Δφ des Rädchens:
Textabbildung Bd. 141, S. 30
folglich auch für ihre Summe
Textabbildung Bd. 141, S. 30
Mein Beweis ist daher nur für die durch gekränkte Eigenliebe getrübte Anschauung des
Hrn. Amsler unrichtig, zu dessen Beruhigung ich noch
bemerken will, daß ich überhaupt niemals Differentiale
miteinander verwechsle, da ich nur mit Differentialquotienten rechne.
Was nun die Bewegung des Rädchens betrifft, so ist Hr. Amsler, welchem ich hier in seine Vorstellungsweise folgen will, sehr im
Irrthum, wenn er meint, es sey dasselbe bei seinem Instrumente den nämlichen
Bedingungen unterworfen, wie bei dem Wetli'schen und
solchen Polar-Planimetern, bei denen die Achse des Rädchens immer durch den
Pol geht. Bei diesen letztern dreht sich das Rädchen allerdings um eine und zwar um eine feste verticale Achse, bei dem Amsler'schen aber um zwei
verticale Achsen, eine bewegliche B und eine feste C; es bewegt sich also in einem Epicykel, und dadurch wird eben seine Bewegung eine zusammengesetztere.
Bei dem Wetli'schen, dem Bouniakovsky'schen und meinem Planimeter ist die
Bewegung des Rädchens in Bezug auf seine Unterlage von vollkommen gleicher
Beschaffenheit; bei dem erstern schiebt sich die Achse der Scheibe (der Pol
für das Rädchen) in der Achse des Rädchens hin und her, und die Scheibe dreht sich
unter dem Rädchen, bei den letzteren ist der Pol und die Scheibe (die Unterlage)
fest und das Rädchen mit seiner Achse in der Art beweglich, daß seine Achse immer
die feste Achse schneidet und sich gleichsam in dieser verschiebt. Die Behauptung
des Hrn. Amsler, die praktischen Uebelstände in Betreff
bestimmter Figuren seyen bei dem Bouniakovsky'schen und
meinem Planimeter am schwierigsten, bei dem Wetli'schen
am vollständigsten zu beseitigen, das seinige halte die Mitte ein, klingt daher
etwas lächerlich. Wenn derselbe ferner sagt: „die Natur jener Bewegung
hängt offenbar durchaus nicht davon ab, u.s.w., wie man sie wirklich
hervorbringt“, so weiß ich nicht, was damit in Bezug auf das
Instrument überhaupt und insbesondere unter „Natur jener
Bewegung“ gemeint seyn soll. Die richtige
Angabe des Instrumentes oder die richtige Drehung des Rädchens, um welche
es sich hier handelt, hängt allerdings davon ab, wie die Bewegung des Rädchens
hervorgebracht wird, und es ist gar nicht gleichgültig, wie Hr. Amsler weiter meint, welche Bewegungen zur Führung des
Rädchens benützt werden; denn es handelt sich hier nicht allein um die Gestalt der
Bahn seines Berührungspunktes, welche für eine zu berechnende Figur bei jedem anders
construirten Planimeter eine andere ist, sondern, wie Hr. Amsler selbst bemerkt, hauptsächlich um die Stellung der Achse des
Rädchens in Bezug auf die Bahn des Berührungspunktes, oder darum, ob das Rädchen
seinen Weg mehr gleitend oder mehr wälzend zurücklegt, und dann darum, ob dasselbe
keine nutzlosen Bewegungen macht. Es ist daher dasjenige Instrument das minder zuverlässige, bei
welchem der Winkel zwischen der Bahn-Tangente und der Achse des Rädchens
meistens kleiner ist als 45° oder bei welchem das Rädchen den größeren Theil
seines Weges gleitend zurücklegt und mehr nutzlose Bewegungen macht; daß dieses aber
unter den obigen Instrumenten gerade das Amsler'sche ist,
davon wird man sich ohne lange Untersuchung durch einen Blick auf die Figuren 24,
25, 26 und 27 überzeugen,
welche die Wege des Berührungspunktes und die Lage der Achse des Rädchens bei dem
Amsler'schen und meinem Planimeter für gleiche
Figuren darstellen, und welche zeigen, daß bei dem ersteren der Berührungspunkt
selbst für die günstigste Figur, den Kreis, eine sehr langgestreckte Bahn beschreibt
und von dieser einen viel größeren Theil gleitend als wälzend zurücklegt.Die Figur
24 kann auch dazu dienen, die Lage der Flächen-Elemente des
Hrn. Amsler deutlich zu machen, und die Frage zu
beantworten, ob man darnach so geradezu behaupten kann, daß die Summe dieser
innerhalb und außerhalb des Kreises sich kreuzenden positiven und negativen
Elemente der Fläche des Kreises gleich sey. Ebenso wird es mit allen dem Kreise nahe kommenden Vielecken und noch mehr
mit länglichen Figuren der Fall seyn; beachtet man dann noch, daß bei diesem
Planimeter das Rädchen einen ziemlich bedeutenden Weg nutzlos abwälzt, nämlich den
Weg: (a² + b²
+ 2ac)/2a (ω₁ – ω₀), welcher für alle Figuren außerhalb des Poles einmal in
positivem und dann in negativem Sinne gemacht werden muß, und daß eine solche
nutzlose Drehung, welche immer auch eine entsprechende nutzlose gleitende Bewegung
mit sich bringt, eine neue, nicht unbedeutende Fehlerquelle ist, so wird kaum noch
ein Zweifel darüber bestehen können, daß das Princip des Amsler'schen Planimeters bei aller Sorgfalt der mechanischen Ausführung
nicht geeignet ist, ein möglichst zuverlässiges
Instrument zu liefern, und dieß war es, was ich durch die Erörterungen in meinem
früheren Aufsatze, welche sich auf mechanische, nicht auf „unklare
geometrische“ Betrachtungen stützen, und welchen Hr. Amsler alle Realität abspricht, zeigen wollte, wobei ich
mich aber allerdings auf einen andern Standpunkt stellte, als auf den der
Anwendbarkeit zur Berechnung von Querprofilen und Grund-Entschädigungen. Für
solche Zwecke erkenne ich die Brauchbarkeit und wegen bedeutender Zeitersparniß auch
die große Nützlichkeit des Polar-Planimeters gerne an.
Für die Bemühung des Hrn. Amsler, mein Planimeter zu
verbessern, bin ich demselben sehr dankbar, bedauere aber, die Modification desselben nicht als eine
zweckmäßige Verbesserung anerkennen zu können, da die Führung des Rädchens durch die
Verbindungsschiene JH, Fig. 28, ganz
unzuverlässig wird, wenn H in die Nähe von D kommt, und weil die Schiene JH dabei einen sehr nachtheiligen Druck auf CD ausübt.
Wenn die Achse des Rädchens nicht durch C geht, sondern
nur zu CD parallel ist, so muß man der Angabe des
Instrumentes für Figuren, welche den Pol einschließen, noch eine Constante
beifügen.
Tafeln