| Titel: | Beiträge zur Bestimmung des richtigen Röhren-Durchmessers und des Minimalgefälles der Drains. |
| Autor: | v. Möllendorff, Waege, E. John |
| Fundstelle: | Band 138, Jahrgang 1855, Nr. LXVIII., S. 257 |
| Download: | XML |
LXVIII.
Beiträge zur Bestimmung des richtigen
Röhren-Durchmessers und des Minimalgefälles der Drains.
Mit Abbildungen auf Tab.
VI.
Ueber Bestimmung des Röhren-Durchmessers der
Drains.
Der entschiedene Einfluß, den die Wahl des richtigen Durchmessers der Röhren auf die
erfolgreiche Wirkung und die zu hoffende Dauer einer Drainanlage ausübt, darf als
allgemein bekannt vorausgesetzt werden.
Ist der Durchmesser einer Röhrenleitung so klein, daß die zu bewältigende Wassermasse
in dem zur Trockenlegung des Grundstücks festgesetzten Zeitraume nicht abgeführt
wird, so ist die beabsichtigte Wirkung verfehlt, denn der Boden bleibt länger naß,
als für zuträglich erachtet war. Ist der Durchmesser so groß, daß die Röhren
jährlich nicht ein- oder einigemale vollfließen und dadurch von den
Boden- und Ocker-Ablagerungen gereinigt werden, so ist für. die Dauer
der Anlage zu fürchten, denn es werden nach längerer oder kürzerer Zeit
Verstopfungen eintreten.
Bei der Berechnung des anzuwendenden Röhrendurchmessers sind drei Momente zu
berücksichtigen:
1) die Ermittelung der abzuführenden Wassermenge;
2) die Feststellung des Zeitraums, binnen welchem das Wasser aus
dem Boden entfernt werden soll, und
3) die Berechnung der Geschwindigkeit, mit welcher das Wasser in
den Röhren unter den verschiedenen Gefällverhältnissen abläuft.
Hier soll nur der letztere Punkt ins Auge gefaßt werden.
Jeder wissenschaftliche Draintechniker kennt die hydrostatischen Formeln zur
Berechnung der Abflußgeschwindigkeit in Röhrenleitungen, und weiß daß ein aus
angestellten Versuchen hergeleiteter Contractions-
und Widerstands-Coefficient die hypothetische in
die wirkliche Geschwindigkeit verwandelt. Diese von
gelehrten Forschern aufgestellten Formeln beziehen sich aber sämmtlich auf Metallröhren ohne Unterbrechung, nicht auf Thonröhren, die von
Fuß zu Fuß aneinander gereiht sind, und welche durch ihre rauheren
Wandungen und durch die Stauung an den Stoßfugen dem Wasserabflusse einen größern
Widerstand entgegensetzen, als die metallenen Röhren.
Da die in der Eytelwein'schen Formel:
Textabbildung Bd. 138, S. 257
enthaltenen Größen, von welchen c die Geschwindigkeit des
Wasserablaufes pro Secunde, d den Röhrendurchmesser, h die Gefällhöhe, l die Länge der Leitung bedeutet, sich durchgängig auf
preußische Duodecimalfuße beziehen, so ist in der Regel diese Formel als die
bequemste und auch für den Zweck genügend genaue, von den preußischen
Drain-Ingenieuren mit Rücksicht auf den größeren Widerstand modificirt und
der Geschwindigkeitsberechnung für Drainröhrenleitungen untergelegt worden.
Natürlich mußten die von verschiedenen Technikern gemachten gutachtlichen
Modificationen auch verschiedenartige Resultate ergeben, weil dieselben nur auf
Annahmen, nicht aber auf directen Versuchen beruhen, und deßhalb können die von Vincent in seiner „Theorie und Praxis der
Drainage“ Seite 36 und von Stocken in Nr.
9 der Zeitschrift „für deutsche Drainirung und andere landwirthschaftliche
Meliorationen“ Jahrgang 1852 vorgeschlagenen Reductionen nicht
genügen.
Da bis jetzt Experimente zur Ermittelung des Coefficienten nicht angestellt,
wenigstens nicht veröffentlicht worden sind, so mußte, um den unsicheren
gutachtlichen Annahmen nicht noch neue hinzuzufügen, durch inductive Versuche eine
Grundlage' erstrebt werden.
Die behufs dessen von den Unterzeichneten angestellten Versuche zerfallen insofern in
zwei Reihen, als der erforderliche constante Wasserspiegel bei der ersten Reihe in
einem kleineren Wasserbehälter, nämlich einem Holzgefäße, bei der anderen in einem
größeren, nämlich einem Mühlteiche, hergestellt wurde.
I. Reihe. Der Apparat, welcher bei den auf der städtischen
Ziegelei zu Görlitz veranstalteten Versuchen angewendet wurde, war folgendergestalt
zusammengesetzt.
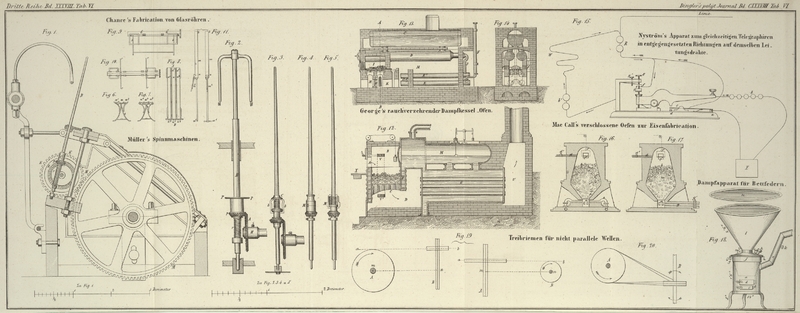
Durch ein Pumprohr a, Fig. 19, wurde das Wasser
aus einem Teiche in die Rinne b gehoben, und in dieser
bis in das obere, auf einem Gestelle ruhende Reservoir A
fortgeleitet. Der unmittelbar vor demselben auf dem Erdboden stehende Regulator B empfing seine Füllung aus dem Reservoir A durch ein Spundloch c,
welches durch einen langen, conisch gearbeiteten Zapfen, je nach der erforderlichen
vergrößerten oder verringerten Abströmung, mehr oder weniger geöffnet oder ganz
geschlossen werden konnte. In die Oberkante der Seitenwand des Regulators B war eine halbrunde Oeffnung d geschnitten, welche eine nicht ganz 2 Ruthen lange Rinne f aufnahm und unbeweglich festhielt. Das andere Ende g der Rinne konnte durch die Winde w auf und nieder gehoben werden, und wurde auf jeder
Seite durch einen in die Erde getriebenen Pfahl p vor
seitlichen Verschiebungen gesichert. In die Rinne f
wurden 24 Stück Drainröhren hart an einander, wie in Draingräben, gelegt und mit nassem Thon gut
verstrichen, so daß kein Wasser aus den Stoßfugen hervordringen konnte. Das erste
Rohr ragte einen Zoll über die innere Wand des Gefäßes B
bei der Oeffnung d heraus, das letzte am Rinnenende g ebenfalls einige Zoll über den Endpunkt der Rinne. Der
Recipient oder Wassermesser (C) am Ufer des Teiches,
nach welchem hin das Terrain Abfall hatte, stand unter dem Rinnenende g und war mit einem Spundloche k versehen, um ihn vor Beginn jedes einzelnen Versuches völlig entleeren
zu können.
Dieser Recipient, welcher einen abgestumpften Kegel bildete, hatte eine Tiefe von 24
Zoll, der Durchmesser der oberen Oeffnung enthielt 4 Fuß 7 Zoll, der des Bodens 4
Fuß 3 Zoll.
Die Operation wurde in folgender Weise ausgeführt:
Nachdem die Länge (l) der Röhrenleitung gemessen und
mittelst eines Röhrenlibellen – Niveau's und der Winde w das angenommene Gefälle g sorgfältig
hergestellt war, wurden das Reservoir und der Regulator mit Wasser gefüllt, und die
untere Röhrenmündung bei g so lange verstopft, bis das
in die Röhrenleitung getretene Wasser keine Blasen bei d
zurückwarf und dadurch der Beweis geliefert worden war, daß keine mit Luft gefüllten
Räume in den Röhren mehr vorhanden waren. Jetzt erst erfolgte die Abströmung in den
zuvor völlig geleerten Recipienten C; die Röhrenmündung
bei g wurde geöffnet, dieser Zeitpunkt nach einer
Secunden-Uhr genau notirt, und der Wasserstand in dem als Regulator dienenden
Gefäße B durch größeres oder geringeres Oeffnen des
Spundloches c während der ganzen Dauer des Abflusses in
einer solchen Höhe erhalten, daß der Wasserspiegel mit der äußeren Oberkante der
ersten Drainröhre abschnitt. Hierdurch sollte vermieden werden, daß das Wasser unter
Druck in die Röhren trat. – Endlich ließ man die Röhren so lange fließen, bis
der Wasserstand im Recipienten C eine für den
jedesmaligen Versuch verhältnißmäßig genügende, genau gemessene Höhe erreichte, und
beobachtete diesen Zeitpunkt abermals nach der Secundenuhr, wodurch die ganze Dauer
des Abflusses bis auf die Secunde genau bestimmt war.
Sobald ein Versuch beendet war, wurde das Wasser aus dem Recipienten abgelassen, und
entweder das Gefälle unter Beibehaltung der Röhren mittelst der Winde verändert und
mit dem Nivellirinstrument abgewogen, oder mit Belassung des Gefälles andere
Röhren-Dimensionen in die Rinne f gelegt und
alsdann dasselbe Verfahren wiederholt. – Nachdem sechs Versuche mit zwei
verschiedenen Gefällverhältnissen und drei verschiedenen Röhrendimensionen
unternommen waren, wurde zur Berechnung geschritten. Zunächst war die aufgefangene
Wassermenge zu ermitteln. Bezeichnet R den Halbmesser der Oeffnung, r den Halbmesser des Faßbodens, H die gemessene Höhe des jedesmaligen Wasserstandes im Gefäße C, ferner ρ den zu suchenden Halbmesser des
Wasserspiegels, Q den Kubikinhalt der aufgefangenen
Wassermasse, alles in preuß. Duodecimalfuß, endlich noch t die beobachtete Zeitdauer des Abflusses in Secunden, so ergibt sich, da
die Gefäßtiefe 2 Fuß beträgt,
ρ = (R – r)/2 H
+ r und
Q = 1/3 π
H (r² + ρ² + rρ).
Sodann führten folgende Formelentwickelungen zu den nachstehenden Resultaten.
Als bekannt darf die Herleitung der Formel für die allgemeine
Ausflußgeschwindigkeit
c = 2 √gh
vorausgesetzt werden, in welcher g
die Beschleunigung für den freien Fall schwerer Körper im luftleeren Raume = 15,625
preuß. Duodecimalfuß und h die gesammte Druckhöhe
bedeutet. Hieraus ergibt sich
c = (7,₉₀₅₇ ...) √h.
Bei dem Abflüsse des Wassers durch Röhrenleitungen treten indessen zwei verschiedene Ursachen auf, welche die
Geschwindigkeit vermindern, die eine durch die Zusammenziehung des Strahles beim Eintritte des Wassers in die Röhren, die
andere durch den, vermöge der Reibung des Wassers an den Röhrenwandungen sich
erzeugenden Widerstand.
Es hat nämlich nicht allein die vor der Röhrenöffnung in der Richtung der
Verlängerung der Röhrenleitung befindliche Wassersäule das Bestreben des Abflusses,
sondern es übt auch das zur Seite dieser Säule stehende Wasser einen Druck auf
dieselbe, drängt sich mit unter das abfließende Wasser, bewirkt dadurch eine
Zusammenziehung des in die Röhre tretenden Wassers und hemmt offenbar die freie
Beschleunigung des Abflusses, also die normale Geschwindigkeit. Eine ähnliche
Bewandtniß hat es mit dem in den Drainröhren abfließenden, und während ihres
Vollfließens in dieselben durch die Stoßfugen hinzutretenden Wassers. Denn wenn auch
bei den Drains der Wassereintritt nicht wie aus einem Gefäße oder Teiche mit einem
male am Anfange der Leitung in dem vollen Querschnitte des Rohrs erfolgen kann,
sondern sich die abströmende Masse erst allmählich ansammelt, und endlich durch
fortwährenden Zudrang zwischen den Stoßfugen anschwillt bis zur vollständigen
Füllung der Röhren, so ist zwar eine Zusammenziehung des eintretenden Wassers in der
oben angedeuteten Art nicht vorhanden, aber die durch die Röhren fließende Wassersäule erleidet von
Fuß zu Fuß an jeder Stoßfuge, die es zu überschreiten hat, einen in diesen kurzen
Zwischenräumen sich fortwährend wiederholenden verticalen und Seitendruck durch
dasjenige Wasser, welches sich unter die Strömung mengt und hierdurch eine Ablenkung
von der geraden Richtung derselben herbeiführt. Es erscheint daher einleuchtend, daß
es gleichgültig seyn muß, ob die das Rohr füllende Wassermasse gleich beim ersten
Eintritte in die vordere Oeffnung den Druck des Seitenwassers in dessen ganzer Menge
erfährt und dann ungestört weiterfließt, oder ob ein in bestimmten Unterbrechungen
wiederkehrender Zudrang dergestalt stattfindet, daß der in Bewegung befindliche
Wasserstrom denselben mit aufnehmen und fortführen muß. Mithin kann die Verminderung
der Geschwindigkeit bei Röhrenleitungen, welche ihre Speisung an ihrem oberen vollen
Querschnitte empfangen, als gleich groß betrachtet werden mit der Verminderung der
Abflußgeschwindigkeit in Drainröhren, weil dieselbe bei beiden aus gleichen Ursachen
entspringt.
Hiernach ist es klar, daß nicht mehr der für den freien Fall berechnete Coefficient
7,₉₀₅₇ in der Formel für die Abflußgeschwindigkeit in
Röhrenleitungen zur Anwendung gebracht werden kann, sondern daß ein anderer, ein
Erfahrungs-Coefficient, an dessen Stelle treten muß, welcher mit α bezeichnet und Contractions-Coefficient genannt wird.
Ebenso bedarf es auch zur Bestimmung des Einflusses, welchen die Reibung des Wassers
an den Röhrenwandungen ausübt, eines zweiten Erfahrungs-Coefficienten,
welcher durch 1/β² ausgedrückt werden soll
und unter der Bezeichnung Reibungs- oder Widerstands-Coefficient bekannt ist.
Die gesammte Druckhöhe h äußert daher ihre Wirkung nach
zwei verschiedenen Richtungen, einmal, indem sie den Eintritt des Wassers in die
Röhren vermittelt und auf die Zusammenziehung des Strahls influirt, das anderemal,
indem sie die Hindernisse an den Röhrenwandungen zu überwinden hat. Wird nun
derjenige Theil der Druckhöhe, welcher die ersten Function erfüllt, mit h', der andere aber mit h''
bezeichnet, so ist die gesammte Druckhöhe
1) h =
h' + h''
und es entsteht
c = α √h' oder
2) h' =
c²/α².
Der Widerstand, den das Wasser beim Durchlaufen der Röhren erfährt, ist proportional
der Länge (l) der Röhren, proportional dem Quadrat der
Geschwindigkeit (c²) und steht im umgekehrten
Verhältnisse mit dem Durchmesser (d) der Röhren, woraus
folgt:
3) h'' =
1/β² . c²l/d,
daher
4) h =
c²/α² + 1/β² . c²l/d, also
5) Textabbildung Bd. 138, S. 262
Du Buat hat aus 51 Versuchen mit Metallröhren für den
Widerstands-Coefficienten 1/β² den
Mittelwerth 1/44,₇₉² gefunden; wird derselbe für 1/β² eingesetzt, so ergibt sich
Textabbildung Bd. 138, S. 262
Nach Eytelwein's Untersuchungen ist der
Contractions-Coefficient α auf
6,₄₂ festgestellt worden, und man erhält durch Substitution
Textabbildung Bd. 138, S. 262
oder ziemlich nahe die Eingangs erwähnte bekannte Formel:
Textabbildung Bd. 138, S. 262
Der Wassereintritt in die Röhren findet jederzeit in durchaus gleicher Weise statt,
mag die Leitung aus metallenen, hölzernen oder gebrannten Röhren bestehen, weßhalb
der Contractions-Coefficient stets derselbe seyn wird. Es ist daher
einflußlos auf die Sache, ob Eytelwein bei seinen
Versuchen zur Ermittelung des Contractions-Coefficienten das eine oder das
andere Material verwendete, die von ihm gefundene Größe 6,₄₂ mußte
unter jeder Bedingung für jedes Röhrenmaterial als dieselbe hervorgehen und muß
daher auch für Drainröhrenleitungen beibehalten werden.
Dagegen ändert sich die größere oder geringere Reibung, und es vermehrt oder
vermindert sich der dem Wasserlaufe entgegen tretende Widerstand, je nach der
Unebenheit oder Glätte des Materials, aus welchem die Röhren bestehen, und daher ist
es der von du Buat aus seinen Experimenten mit
Metallröhren gefundene Widerstands-Coefficient, welcher zur Umwandlung für
Drainröhren gebracht werden muß und von uns in dem vorliegenden Falle durch Berechnung folgendermaßen
gesucht worden ist.
Da nämlich Q aus dem Producte des Querschnittes der
Röhrenleitung und der Geschwindigkeit des Wasserlaufes sich ergibt,
der Querschnitt = d²/4
π
die beobachtete Zeit = t Secunden
und die Geschwindigkeit = c ist,
so entsteht
Textabbildung Bd. 138, S. 263
und hieraus
6) Textabbildung Bd. 138, S. 263
Nach dieser Formel wurden die durch die Versuche auf der Görlitzer Ziegelei
erhaltenen Resultate berechnet.
Leider gewährte die Berechnung kein befriedigendes Resultat, sondern ließ
unzweifelhaft erkennen, daß trotz des Regulators B ein
Druck auf das in die Röhrenleitung eingetretene Wasser ausgeübt worden war, weil in
ihm eine drehende Bewegung des Wassers durch den comprimirten Ausfluß aus dem
Reservoir A stattgefunden hatte.
Genöthigt durch das Mißglücken dieses ersten Experimentes, mußte dasselbe wiederholt
werden. Um aber den störenden Druck aufzuheben, wurde nunmehr zum Schütze des
Wassereintritts in die Röhren ein aus drei 10 Zoll breiten Brettern rechtwinkelig
zusammengefügter Vorsetzer v, dessen Länge mit der Höhe
des Gefäßes B übereinstimmte, angefertigt und mit seiner
offenen Fläche dergestalt vor die Abflußöffnung d
gebracht, daß bis zum Boden des Gefäßes nur ein Raum von 1/4 Fuß verblieb, um die
Verbindung zwischen dem innerhalb und außerhalb des Vorsetzers befindlichen Wasser
frei zu erhalten. Außerdem wurde noch der Strahl aus dem Spundloche c durch einen Besen aufgefangen, um die Kraft der
Zuströmung möglichst zu brechen. Hierdurch erlangte man innerhalb des Vorsetzers und
vor der Einmündung der Röhren einen vollkommen ruhigen Wasserspiegel. Unter dieser
Vorsichtsmaßregel wurden folgende sieben Versuche mit drei verschiedenen
Röhrendimensionen zu 1 5/6'' = 7/64', zu 1 7/8'' = 5/32' und zu 2 7/8'' = 23/96'
Durchmesser, sowie unter den verschiedenen Gefällverhältnissen von 6, 12, 18 und 30
Zoll Fall auf 10 Ruthen Länge ausgeführt.
Erster Versuch.
Länge der Röhrenleitung
l
= 23,₁ Fuß
Röhrendurchmesser
d
= 23/96 „
Gefälle 12 Zoll auf 10 Ruthen,
also
h
=
0,₁₉₃ „
Wasserhöhe im Gefäße C, d. i.
H
= 20 Zoll
Zeitdauer des Abflusses
t
= 373 Secund.
hieraus berechnen sich
Q
= 25,₂₂₃ Kubikf.
und β = 39,₅₈.
Zweiter Versuch.
l = 23,₁'; d =
23/96'; Gefälle 18 Zoll auf 10 Ruthen, folglich h =
0,₂₉₅'; H = 20''; t = 260 Sec., mithin Q =
25,₂₂₃ Kubikf.
und β = 49,₄₃.
Dritter Versuch.
l = 23,₆'; d = 5/32';
Gefälle 18 Zoll auf 10 Ruthen, folglich h =
0,₂₉₅'; H = 15''; t = 672 Sec., mithin Q =
18,₆₁₅ Kubikf.
und β = 35,₉₁.
Vierter Versuch.
l = 23,₆'; d = 7/64';
Gefälle 18 Zoll auf 10 Ruthen, folglich h =
0,₂₉₅'; H = 12''; t = 974 Sec., mithin Q =
14,₇₅ Kubikf.
und β = 49,₁₅.
Fünfter Versuch.
l = 23,₆'; d = 7/64';
Gefälle 12 Zoll auf 10 Ruthen, folglich h =
0,₁₉₇'; H = 12''; t = 1180 Sec., mithin Q =
14,₇₅ Kubikf.
und β = 49,₇₉.
Sechster Versuch.
l = 23,₆'; d = 7/64';
Gefälle 30 Zoll auf 10 Ruthen, folglich h =
0,₄₉'; H = 13''; t = 857 Sec., mithin Q = 16,₀₃
Kubikf.
und β = 46,₆₀.
Siebenter Versuch.
l = 23,₆'; d = 7/64';
Gefälle 6 Zoll auf 10 Ruthen, folglich h =
0,₀₉₈'; H = 6''; t = 1080 Sec., mithin Q =
7,₂₃₃ Kubikf.
und β = 35,₇₇.
Die Summe dieser sieben Coefficienten ist = 306,₂₃, also ergibt die
Durchschnittszahl aus den Versuchen der I. Reihe die in dem
Widerstands-Coefficienten enthaltene Größe
β = 43,₇₅.
Hierbei wird bemerkt, daß zu den Versuchen zwar keineswegs die besten Röhren besonders ausgewählt worden waren, daß aber die Fabrication
derselben auf der Görlitzer Ziegelei in großer Vollendung betrieben wird, und sich
die Röhren durch vollkommen glatte innere Wandungen, mittelst Rollens hergestellt,
durch scharfe und glatte rechtwinkelige Schnittflächen ohne die mindeste Spur eines
Grates, durch Stauchen und Putzen erreicht, und durch gleichmäßige Wandungsstärke
auf das vortheilhafteste auszeichnen.
Die nach den ersten sechs Versuchen erkannte Notwendigkeit, einen gleichmäßigen und
ruhigen Wasserspiegel herzustellen, führte außer dem eben beschriebenen noch ein
zweites Verfahren herbei und gab so Veranlassung zu der zweiten Reihe von
Versuchen.
II. Reihe. Diese Versuche wurden am Mühlteiche zu Stenker
bei Rauscha angestellt.
Die Einbettung der Röhren mittelst Thon in eine Holzrinne und die Auffangung und
Messung des durch die Röhrenleitung geflossenen Wassers in einem Recipienten fand
wie bei der I. Versuchsreihe statt. Dagegen bestand das Reservoir- und das
Regulator-Faß in dem Teiche selbst, indem jene Vorrichtung in dem Gerinne
einer der Teichschleußen angebracht, in das oberste Spundbrett ein der Breite der
Holzrinne entsprechender und mittelst eines Schiebers, Fig. 20, s verschließbarer Einschnitt d gemacht und in diesen die obere Oeffnung der Holzrinne f, also auch der Röhrenleitung gelegt worden war. Der
ruhige Wasserspiegel im Teiche mußte in gleicher Höhe mit der obern Culmination der
ersten Röhre stehen und wurde nach Beginn der Versuche in dieser Höhe mittelst
Stellung einer anderen Schleiche desselben Teiches erhalten. Die Rinne und
Röhrenleitung war genau 2 Ruthen lang; sie hatte drei Unterstützungspunkte –
der am Einschnitt im Spundbrette war unverrückbar, die beiden anderen in der Mitte
ihrer Länge und am unteren Ende wurden je nach dem bestimmten Gefälle gehoben oder
gesenkt. Die hier angewandten Röhren waren der Fabrik in Tiefenfurt entnommen,
wurden aus einer größeren Anzahl in den besten Exemplaren ausgewählt, so daß sie,
wenn auch den in Reihe I angewandten Röhren nicht völlig gleichstehend, eine ihrer
vorliegenden Bestimmung entsprechende Güte hatten. Auch hier kommen drei Dimensionen
in Anwendung, im Lichten von 1 7/24, 2 1/4 und 3 1/8 Zoll.
Die Bestimmung des Gefälles und der Zeit geschah wie bei Reihe I. Die beobachtete
Wassermenge war bei allen Versuchen gleich groß und es betrug Q = 11,043 Kubikfuß.
Bei den 1 7/24 zölligen Röhren wurden 5 Gefällverhältnisse – von 10, 15, 20,
25 und 60 Zoll auf 10 Ruthen;
bei den 2 1/4 zölligen Röhren 6 Gefällverhältnisse – von 5, 10, 20, 30, 60 und
75 Zoll auf 10 Ruthen;
bei den 3 1/8 zölligen Röhren 4 Gefällsverhältnisse – von 15, 20, 25 und 30
Zoll auf 10 Ruthen beobachtet.
In gleicher Weise, wie die Versuche der I. Reihe berechnet, ergeben die Versuche
dieser II. Reihe:
LaufendeNummer.
Durchmesser der Röhren.
= d.
Gefälle auf 2 Ruthen.
= h.
BeobachteteWassermenge.
= Q.
Zeit.
= t.
Coefficient. = β.
8
31/288'
0,₁₆₆₆
11,₀₄₃
1140
42,₆₀
9
„
0,₂₅
„
950
41,₅₈
10
„
0,₃₃₃₃
„
836
40,₈₀
11
„
0,₄₁₆₆
„
766
39,₆₆
12
„
1,₀
„
492
39,₈₉
13
3/16'
0,₀₈₃₃
„
360
54,₃₉
14
„
0,₁₆₆₆
„
254
54,₅₈
15
„
0,₃₃₃₃
„
193
48,₉₇
16
„
0,₅
„
160
47,₉₀
17
„
1,₀
„
127
40,₈₈
18
„
1,₂₅
„
112
41,₆₅
19
25/96'
0,₂₅
„
115,₅
41,₅₈
20
„
0,₃₃₃₃
„
112
35,₃₃
21
„
0,₄₁₆₆
„
101,₅
34,₉₂
22
„
0,₅
„
70,₅
52,₄₂
–––––––
657,₃₅
Durchschnitt
43,₈₂
Aus beiden Reihen der Versuche geht somit ein fast völlig übereinstimmendes Resultat
hervor, denn während die sieben Versuche
I. Reihe im Durchschnitte
β =
43,₇₅
geben, geht aus den 15 Versuchen II.
Reihe
β =
43,₈₂
hervor, und es beträgt nach dem Durchschnitte sämmtlicher 22
Versuche
der Widerstands-Coefficient für normale
Drainröhren
1/43,₈².
In Formel 5) für β den Werth von
43,₈² eingesetzt, gibt
Textabbildung Bd. 138, S. 267
Diese Formel wird nunmehr der Röhrenberechnung so lange zu Grunde zu legen seyn, bis
anderweite, von Sachkundigen angestellte zuverlässige
Versuche eine gewiß nur erwünschte Berichtigung, resp. Bestätigung herbeigeführt haben werden.
Mit dem größten Danke würde es von allen Drainern anerkannt werden müssen, wenn sich
Hydrauliker von Fach geneigt finden wollten, im
Interesse der Landescultur ähnliche und bessere Versuche anzustellen und die
Resultate in der „Zeitschrift für die deutsche Drainirung“ zu
veröffentlichen.Der mit unterzeichnete Hr. Dr E. John, welcher die „Zeitschrift für die
deutsche Drainirung und andere landwirtschaftliche
Meliorationen“ mit Benutzung der Acten des königl. preuß.
Ministeriums für landwirtschaftliche Angelegenheiten herausgibt, hat aus Nr.
9 und 11 derselben diese Abhandlung für das polytechn. Journal
mitgetheilt.A. d. Red.
Die Unterzeichneten geben nunmehr eine praktische Anwendung des ermittelten
Coefficienten, welche auch ohne ein näheres Eingehen auf die Eingangs sub 1 und 2 erwähnten Gesichtspunkte möglich
erscheint.
Es betrifft dieß
die Berechnung des Minimalgefälles
für die verschiedenen, in Anwendung kommenden
Röhrendimensionen.
Die Praxis hat nämlich vielfach ergeben, daß Drainröhren bestimmter Dimension bei
schwachem Gefälle ihren Dienst nicht sowohl deßhalb versagen, weil die durch sie
abzuführende Wassermasse zu groß gegenüber ihrem lichten Durchmesser und ihrem
Gefälle ist, sondern deßhalb, weil in Folge des zu langsamen Wasserlaufes in ihrem
Innern Sinkstoffe – Sand, Ocker, Wurzelfasern – sich ablagern und die
Röhren verstopfen können. Gestützt auf vielfache Beobachtungen, glauben wir die
Geschwindigkeit des Wasserlaufes von 1/2 Fuß in der Secunde
als die Minimal-Geschwindigkeit, bei
welcher das Wasser noch im Stande ist feinen Sand fortzuführen, annehmen zu
müssen.
Da nun h = c²/6,₄₂² + 1/43,₈² . c² l/d und mit
Anwendung unseres Widerstands-Coefficienten die Geschwindigkeit
Textabbildung Bd. 138, S. 268
ist, so ergibt sich für die Mimmalgeschwindigkeit c = 0,₅' das Minimalgefälle
h = 0,₅²/6,₄₂² . (8 +
3,₁ d)/(3,1 d) = (2 +
0,₇₇₅ . d)/(127,₇₇
d)
und berechnet sich nach dieser Formel
das Minimal-Gefälle für 10 Ruthen Länge
für 1
zöllige
Röhren
auf 2,33 Zoll
„ 1
1/4
„
„
„ 1/88
„
„ 1
1/2
„
„
„ 1/58
„
„ 2
„
„
„ 1,20
„
„ 3
„
„
„ 0,82
„
„ 4
„
„
„ 0,63
„
„ 5
„
„
„ 0,52
„
„ 6
„
„
„ 0,44
„
„ 7
„
„
„ 0,39
„
„ 8
„
„
„ 0,35
„
Hierzu bemerken wir, daß diese Zahlen die volle Anwendung nur bei solchen Drains
finden dürfen, welche aus eben so guten und mit derselben Sorgfalt an einander
gereihten Röhren gebildet werden, wie für die Ermittelung des Coefficienten in
Anwendung kamen. Von beiden Momenten wird in der Praxis oft abgewichen werden:
häufig kommen mangelhafte Röhren in Anwendung, und ihr Legen ist theils in Folge von
Ungeschicklichkeit der Arbeiter, theils in Folge von ungünstiger Beschaffenheit der
Grabenwandungen ein schlechteres. Hierzu kommt, daß bei Röhren mit schlechten
Schnittflächen nicht allein feiner, sondern auch gröberer Sand durch die Stoßfugen
in die Drains tritt; dieser bedarf aber behufs Fortführung eines stärkeren
Wasserlaufes und Gefälles, als der jener Zahlenreihe zu Grunde liegende feine
Sand.
In Zahlen können die durch diese Mängel bedingten Abweichungen von den auf normale Verhältnisse basirten Angaben nicht ausgedrückt
werden; Drainer, welche sich denselben nicht zu entziehen wissen, kommen somit auf
das böse Gebiet des Schätzens.
v. Möllendorff.
Waege.
E. John.
Tafeln