| Titel: | Beschreibung eines Apparates, mit Hülfe dessen man beliebige Gegenstände perspectivisch mit der größten Schärfe aufzunehmen im Stande ist; von W. Hansen. |
| Autor: | W. Hansen |
| Fundstelle: | Band 130, Jahrgang 1853, Nr. I., S. 1 |
| Download: | XML |
I.
Beschreibung eines Apparates, mit Hülfe dessen
man beliebige Gegenstände perspectivisch mit der größten Schärfe aufzunehmen im Stande
ist; von W.
Hansen.
Mit Abbildungen auf Tab.
I.
Hansen's Stereograph.
Ein Jeder, der sich mit der perspectivischen Aufnahme von Landschaften oder
insbesondere von Gebäuden und dergleichen Gegenständen beschäftigt hat, weiß mit
welchen Umständen und Schwierigkeiten diese Arbeiten, wenn sie nur mit einiger
Schärfe ausgeführt werden sollen, verknüpft sind; ich glaube daher hoffen zu dürfen,
daß denen, welche sich mit dergleichen Arbeiten beschäftigen, die Bekanntschaft mit
einem einfachen Instrumente, mit Hülfe dessen sie sicher und bequem zu arbeiten im
Stande sind, nur willkommen seyn wird.
Zwar sind wir schon im Besitze mehrerer solcher Zeichnenapparate, deren Einrichtung
auf den Principien der Optik beruht, wie z.B. camera lucida,
camera obscura u.s.w., allein diese Einrichtungen haben sich unpraktisch
erwiesen und werden daher nirgends ernstlich angewendet, was seinen Grund
hauptsächlich darin haben mag, daß man das Schattenbild nicht auf dem Papiere zu
fixiren vermag und man die Bleistiftstriche nicht von den Schattenlinien
unterscheiden kann; es trifft sich daher nicht selten, daß man die schönste
Zeichnung gemacht zu haben glaubt und nach der Enthüllung statt dessen nur ein
unregelmäßiges Gewirre von krummen Linien aller Art zu sehen den Verdruß hat.
Unter dem Apparat, welchen ich im Folgenden beschreiben und den ich der Kürze halber
Stereograph nennen werde, darf man sich nicht etwa
ein Instrument vorstellen, welches ohne Weiteres eine fertige Zeichnung liefert,
sondern der Zweck desselben ist lediglich der, dem Künstler hauptsächlich bei
Aufnahme von Gebäuden und dergleichen Gegenständen in Hinsicht der Perspective in
dem Grade der Vollkommenheit zu Hülfe zu kommen, daß derselbe mit diesem Instrumente
nicht nur die Punkte, welche er für den perspectivischen Theil der Arbeit
vorzugsweise braucht, aufzutragen im Stande ist, sondern daß er auch aus den
Dimensionen der so erhaltenen Projection mit hinreichender Sicherheit auf die
Dimensionen des projicirten Gegenstandes schließen kann.
Der Stereograph würde alsdann für den Architekten das seyn, was für den Feldmesser
der Theodolit ist.
Bei der Construction eines solchen Instrumentes muß man sich natürlicherweise zuerst
Rechenschaft von dem, was man sich unter der perspectivischen Aufnahme eines
Gegenstandes denken soll, ablegen, und wenn man dieses gethan hat, so ergibt sich
die Einrichtung des Stereographen ganz von selbst. Denken wir uns für diesen Zweck
von unserem Auge aus nach den verschiedenen Punkten des aufzunehmenden Gegenstandes
gerade Linien gezogen und denken uns durch diesen so entstandenen Strahlenbüschel
eine senkrechte Ebene, etwa die Ebene eines Papieres gelegt, so sind die Punkte, in
welchen jene von unserem Auge ausgehenden geraden Linien das Papier treffen, die
entsprechenden Punkte der Projection.
Wäre der projicirte Gegenstand z.B. ein Gebäude und hätte man jene Linien nach den
verschiedenen an dem Hause sich zeichnenden Eckpunkten gezogen, so brauchte man die
so auf der Ebene des Papieres erhaltenen Schnittpunkte dieses idealen
Strahlenbüschels nur durch die entsprechenden geraden oder krummen Linien zu
verbinden, um die vollständige perspektivische Aufnahme zu erhalten.
Es kommt demnach nur noch darauf an, Mittel und Wege zu finden, auf welchen man diese
Arbeit in der Wirklichkeit ausführen kann.
Für diesen Zweck bedienen wir uns am vortheilhaftesten eines um einen Punkt drehbaren
Fernrohrs mit gebrochener optischer Achse, so daß man seitwärts hindurch sehen kann,
und in deren Verlängerung eine verschiebbare Stahlnadel angebracht ist.
Stellt man nun die einzelnen Punkte des Gegenstandes, welchen man projiciren will, in
das Fadenkreuz dieses obenerwähnten Fernrohrs ein und sticht nach jeder Einstellung
in ein hinter letzterem vertical aufgestelltes Papier mit Hülfe jener Stahlnadel ein
feines Loch, so erhält man nach Vollendung dieser Arbeit die Lage aller der Punkte,
welche für den perspectivischen Theil der Zeichnung nöthig sind, und es ist die
Sache des betreffenden Künstlers, diese Punkte durch die entsprechenden Linien zu
verbinden und das Uebrige zur Vollendung der Zeichnung zu thun.
Insofern wäre der erste Theil unserer Aufgabe, nämlich ein Instrument zu construiren,
mit Hülfe dessen man eine genaue perspectivische Aufnahme eines Gegenstandes zu
erhalten im Stande ist, gelöst.
Nun aber ist leicht einzusehen, daß wenn man in Besitz einer solchen Zeichnung ist
und die Verhältnisse kennt, in welchen dieselbe verfertigt worden ist, man aus den
einzelnen Dimensionen der Zeichnung auf die entsprechenden Dimensionen des
aufgenommenen Gegenstandes schließen kann. Wie dieß zu machen ist, soll nun im
Folgenden auseinander gesetzt werden.
Ein Punkt ist seiner Lage nach im Raume bestimmt, wenn man seine Coordinaten (X, Y, Z) in Bezug auf ein fest angenommenes
Coordinatensystem kennt. Ist in unserem Falle A, Fig. 33, der
zu bestimmende Punkt, so haben wir, wenn der Ursprung der Coordinaten in O oder im Drehungspunkt des Fernrohres, die Ebene XY aber parallel und die Achse der Z senkrecht zur Projectionsebene xyz liegt, Aa = Y,
ab = X, Ob = Z,
ferner xy = y, zx = x und Oz = z, wenn man die Koordinaten des Punktes A X, Y, Z und die der Projection desselben x, y, z nennt.
Aus der Aehnlichkeit der Dreiecke Aa O und xy O, ferner ab O und xz O folgen unmittelbar folgende Werthe für X, Y
X
Y
Z
===
Z/z xZ/z y Z
. . . . . . . . . (1)
In welchen Gleichungen X, Y und Z unbekannt ist. Um Z zu eliminiren, verrückt
man am bequemsten das Instrument um ein Stück n in der
Z Achse und projicirt den Punkt zum zweitenmale.
Alsdann erhält man, wenn der Ursprung der Coordinaten X',
Y' und Z' wiederum im Drehungspunkt des
Fernrohres liegt, im Uebrigen aber nichts verändert ist,
X'
=
Z'/z' x'
Y'
=
Z'/z' y'
Z'
=
Z'
In Folge der erwähnten Transformation der Coordinaten aber ist:
X'
=
X
Y'
=
Y
Z'
=
Z + n
z'
=
z
und demnach
X'
Y'
Z'
===
(Z + n) x'/z(Z + n) y'/z
Z + n
. . . . . . . . . . . . (2)
woraus man durch Verbindung der Gleichung (1) und (2) für
X
Y
Z
===
xx'/(x – x') . n/z
yy'/(y – y') . n/z
x/(x – x') . n
. . . . . . . . . (3)
erhält.
Kann man aber ungünstiger Ortsverhältnisse halber das Instrument nicht so verrücken,
daß die vorige Transformation stattfinden wird, daß die Gleichung Y = Y' erfüllt wird, so geht
unsere Transformation, wenn ± v die
Niveaudifferenz zwischen beiden Standpunkten bedeutet, in folgende über:
X'
=
X
Y'
=
Y ±
v
Z'
=
Z + n
folglich:
X'
=
(Z + n) x'/z
Y'
=
(Z + n) y'/z ± v
Z'
=
Z + n
und nach der Elimination
X
Y
Z
===
xx'/(x – x') . n/z(ny' + vz)/(y – y') . y/z(ny' ± vz)/(y – y')
= (ny' + vz)/(y – y') . x/z= x'/(x – x') . n y/z=
x'/(x –
x') . n
. . . . . . . . . (4)
Man sieht, daß man für X und Y zwei verschiedene Ausdrücke erhält, je nachdem man den ersten oder
zweiten Werth von Z in die Formeln der Gruppe (1)
einsetzt, und zwar bedient man sich für die Berechnung des X eines Punktes am vortheilhaftesten des ersten Ausdruckes (4), wenn das
X einen größeren Werth besitzt als die Ordinate Y des Punktes; des zweiten Ausdruckes für X bedient man sich am vortheilhaftesten im umgekehrten
Falle, wenn also die Ordinate Y größer ist als die
Abscisse X. Dasselbe gilt natürlich für die Berechnung
des Y eines Punktes. Ist jedoch ± v = 0, so kann man sich von diesen Schwankungen und von
noch anderen Uebelständen, mit denen diese Art der Berechnung behaftet ist, dadurch
befreien, daß man für die Berechnung der Werthe für Z
nicht x und y, sondern die
directe Entfernung des projicirten Punktes vom Augenpunkt, d. i. von dem Punkte, in
welchem die Z Achse die Ebene der Tafel trifft,
einführt. Nennt man diese EntfernungEntferfernung in der großen Zeichnung a, in der kleinen aber
a', so erhält man folgende Ausdrücke:
X
Y
Z
===
na'/(a – a') . x/z
na'/(a – a') . y/z
na'/(a – a')
. . . . . . . . . (5)
Somit ist also die Bestimmung der Lage eines Punktes im Raume mit Hülfe des
Stereographen auf die Messung der Größen
x, y, z, x', y', n
zurückgeführt und die Aufgabe aus den Dimensionen einer auf
die oben angegebene Weise verfertigten Zeichnung auf die Dimensionen des projicirten
Gegenstandes zu schließen, gelöst. Der Vollständigkeit halber werde ich die
Einzelnheiten und die Resultate einer auf diese Weise ausgeführten Arbeit folgen
lassen, vorher aber zur Beschreibung des Instrumentes,
dessen ich mich für diesen Zweck bediente, übergehen.
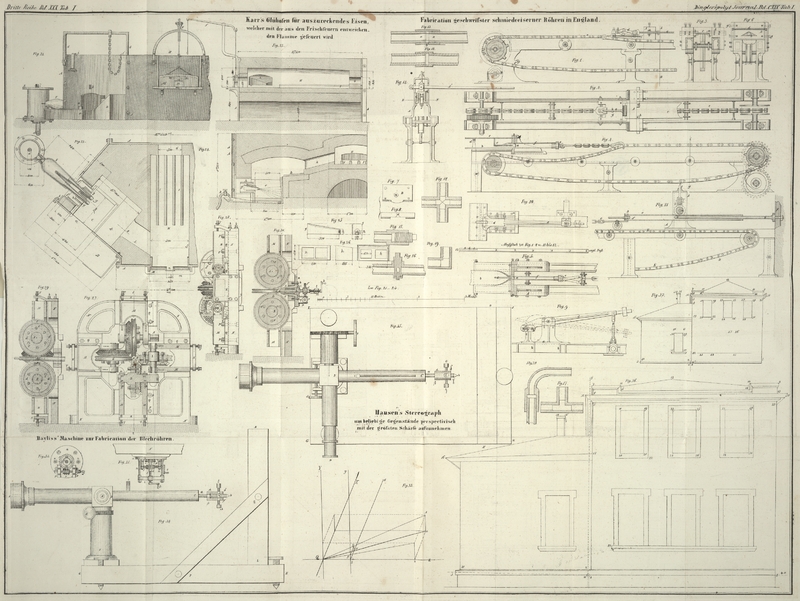
Fig. 34
stellt die verticale Projection des Instrumentes, Fig. 35 die horizontale
Projection dar.
ABD ist das oben erwähnte Fernrohr, dessen
optische Achse sich wie die eines concentrisch befestigten Theodolitenfernrohres um
einen Punkt B, Fig. 35, und D, Fig. 34, dreht, und
außerdem mit einem Prisma versehen ist, so daß man seitwärts hindurchsehen kann.
In der Verlängerung der optischen Achse dieses Fernrohres liegt die Achse des
Cylinders, in welchem die obenerwähnte Stahlnadel a b
vermittelst einer kleinen Handhabe c aus- und
eingeschoben werden kann. Da nun aber viel darauf ankommt, daß sich die Verlängerung
der Stahlnadel um einen Punkt dreht, während der Fehler, der durch eine kleine
Excentricität der optischen Achse hervorgebracht wird, wegen der Entfernung des
aufzunehmenden Gegenstandes verschwinden wird, so muß der Künstler bei der
Ausführung eines solchen Instrumentes seine Aufmerksamkeit hauptsächlich auf diesen
Punkt concentriren.
Sollte sich trotzdem nach der Vollendung durch eine Prüfung, von der ich weiter unten
sprechen werde, ergeben, daß diese oben ausgesprochene Bedingung nicht erfüllt wäre,
was aber, wenn nur einige Sorgfalt auf die Ausführung verwendet worden ist, nicht
der Fall seyn wird, so kann man sich vermittelst einer kleinen Vorrichtung αβγδ, Fig. 34 und 35, welche
dazu dient die Spitze b durch die Correctionsschrauben
εηϑ in die richtige Lage
zu bringen, helfen.
Um das Fernrohr leicht in jede beliebige Lage bringen zu können, sind zwei Schrauben
ohne Ende mit einer Vorrichtung zum Ein- und Auslösen, die Schraube d für die horizontale und e
für die verticale Drehung angebracht. Fig. 34 und 35.
Der Fuß F dieses Fernrohres ist mittelst Schrauben, die
man leicht und ohne Hülfe eines Schraubenziehers losschrauben kann, auf der
hölzernen Platte GH, Fig. 34, und GHIK, Fig. 35, befestigt.
LM, Fig. 34, und NO, Fig. 35, ist die
Projectionstafel, auf welcher das Papier für die Zeichnung befestigt wird. Des
bequemen Zusammenpackens halber ist diese Fußplatte GH, Fig.
34, durch ein Gelenk verbunden. Damit aber diese Tafel nach dem
Auseinanderklappen in der bestimmten Lage stehen bleibt, wird sie durch zwei
metallene Stege, von denen einer in Fig. 34 mit P, Q bezeichnet ist, verbunden.
Einiges Nähere über den Gebrauch des
Stereographen.
Bedient man sich des Instrumentes nur für den Zweck eine perspectivische Aufnahme von
einem Gegenstand, ohne Rücksicht auf die wahren Dimensionen desselben zu erlangen, so ist für diesen Fall
eben weiter nichts zu sagen, als daß man das Instrument so aufstellt, daß die
Normale der Projectionstafel, welche das Centrum des Fernrohres trifft, durch den
vorher gewählten Augenpunkt geht; alsdann beginnt man mit der eigentlichen Arbeit,
d.h. man stellt das Fadenkreuz des Fernrohrs auf die Punkte des aufzunehmenden
Gegenstandes, welche hauptsächlich die Gestalt und Lage desselben bestimmen, ein,
und sticht jedesmal mit der oben beschriebenen Nadel ein kleines Loch in das auf der
Projectionstafel aufgestellte Papier. Ist man hiermit zu Ende gekommen, so verbindet
man die so erhaltenen Punkte durch die entsprechenden Linien.
Hat man aber die Absicht eine mit diesem Instrumente gemachte Zeichnung weiter zu
benutzen und aus derselben die Dimensionen und die Lage des betreffenden
Gegenstandes zu ermitteln, so muß man vor allen Dingen das Instrument, dessen man
sich zu diesem Zweck bedienen will, näher untersuchen. Dazu gehört zunächst jene bei
Gelegenheit der Beschreibung desselben erwähnte Prüfung, welche darauf hinausläuft
zu untersuchen, ob die Verlängerung der Stahlnadel im Drehungspunkt des Fernrohres
liegt.
Die mögliche Abweichung von dieser Bedingung kann von zweierlei Art seyn, nämlich
einmal kann diese Verlängerung außerhalb der verticalen, das anderemal außerhalb der
horizontalen Drehungsachse des Fernrohres liegen. Um beide Fehler kennen zu lernen,
stellt man das Fadenkreuz des Fernrohres auf ein entferntes Object ein, sticht mit
der Nadel in die Projectionstafel ein feines Loch, legt alsdann, wenn sich die
Achsen des Fernrohres, wie bei einem Theodoliten, in sogenannten YY drehen und zum Herausnehmen eingerichtet sind,
das Fernrohr um, so daß letzteres um seine optische Achse um 180° gedreht
wird, stellt das Fadenkreuz wieder auf dasselbe Object ein und sticht wiederum ein
Loch, alsdann ist der erste der gesuchten Fehler, wenn man den horizontalen Abstand
α, den verticalen der beiden Löcher β nennt, 1/2 α
und der zweite Fehler 1/2 β. Wofern α und β nicht
gleich Null sind, hat man α mit Hülfe der
Schrauben η und o,
Fig. 35,
und β mit Hülfe der Schrauben ε und ϑ gleich
zu machen. (Fig.
34.)
Nach Vollendung dieser Arbeit bleibt nur noch jener Abstand des Drehungspunktes des
Fernrohres von der Ebene der Tafel, welchen ich im Vorigen mit z bezeichnet habe, zu messen übrig. Dieß kann auf
directem und indirectem Wege geschehen; ich werde jedoch nur von der Weise, in
welcher die directe Messung auszuführen ist, reden, da diese die zweite bei weitem
an Sicherheit und Einfachheit übertrifft. Zu diesem Zweck bringt man auf irgend eine Weise
in der Mitte der Projectionstafel ein Stückchen Fensterglas oder sonst etwas
dergleichen anHier wird im Stillen vorausgesetzt, daß, wenn die Nadel die Mitte der Tafel
berührt, sie auch senkrecht auf derselben steht., schiebt die Stahlnadel so weit heraus, bis sie das Glas in der Mitte
berührt, dreht alsdann das Fernrohr um seine verticale Drehungsachse um 180°
und mißt den Abstand der Nadelspitze von der Mitte der Glasscheibe; der gesuchte
Werth von z ist alsdann, wenn man d die Dicke der Glasscheibe und l den
gemessenen Abstand nennt:
z = 1/2 l + d
Will man wissen, ob sich beide Drehungsachsen schneiden, was eine wesentliche
Bedingung der Güte und Brauchbarkeit des Instrumentes und außerdem auch ohne
Schwierigkeit auszuführen ist, so braucht man nur dieselbe Operation wie vorhin mit
der Abänderung noch einmal vorzunehmen, daß man das Fernrohr um die horizontale
Achse um 180° dreht. Nennt man den jetzt gefundenen Abstand der Lagen der
Spitze l', so soll, wenn beide Drehungsachsen in einer
Ebene liegen
l – l' = 0.
Sollte diese Bedingung bei der Ausführung nicht erfüllt worden seyn, so kann man sich
damit helfen, daß man, wenn ein bloßes Nachfeilen nicht ausreicht, das eine Y wie bei einem Passageinstrument zum Verschieben
einrichtet, und auf diese Weise mit Hülfe von Correctionsschrauben beide Achsen in
ein Planum einstellt. Uebrigens muß ich noch bemerken, daß die Ausführung aller
dieser kleinen Correctionen, wie auch die Bestimmung von z die Sache des ausführenden Künstlers ist, da man denen, welchen die
Anwendung dieses Instrumentes hauptsächlich von Nutzen seyn wird, nämlich den
Architekten, nicht zumuthen darf, sich mit solchen außer dem Kreise ihrer
gewöhnlichen Beschäftigungen liegenden Dingen zu beschäftigen.
Hat man das Instrument auf diese Weise untersucht, so ist es zum Gebrauche bereit.
Zum Zweck der ersten Aufnahme eines Gegenstandes, z.B. eines Gebäudes, muß man den
Stereographen so nahe als möglich, d.h. so nahe, daß die Projectionstafel eben noch
die ganze Zeichnung zu fassen im Stande ist, vor dem Gebäude aufstellen, die Spitze
der Nadel auf die Mitte der Projectionstafel setzen, das Fernrohr sammt letzterer
mit Hülfe einer kleinen Libelle nivelliren und dann auf den vorher gewählten
Augenpunkt richten, der natürlich so gewählt seyn muß, daß er mit dem Centrum des Fernrohres in einer
Horizontalebene liegt; auch ist es sehr vortheilhaft, wenn der Augenpunkt so gewählt
ist, daß die Projectionstafel parallel mit der einen Wand des Gebäudes und er selbst
in der Mitte der Wand liegt, denn alsdann kann man die berechneten Abscissen
unmittelbar zur Berechnung der Dimensionen verwenden und die ganze Zeichnung wird
gleichmäßig auf der Tafel vertheilt. Hierauf beginnt man mit der schon oben
erwähnten Bezeichnung der Punkte.
Ist man hiermit fertig, so zieht man ein anderes Stück Papier auf die Tafel und
verrückt das Instrument in der schon oben angegebenen Weise in der Z Achse soweit es nur irgend möglich ist, bestimmt, wenn
sich der Standpunkt hinsichtlich der Höhe geändert hat, nach vollendetem Nivellement
den Zahlenwerth von v und trägt, wenn Alles vorbereitet
ist, wiederum die Punkte auf, welche man zur Berechnung der verlangten Coordinaten
braucht; will man nur die Höhe und die Länge des Gebäudes kennen lernen, so braucht
man natürlich nach der zweiten Aufstellung des Stereographen nur 3 oder 4 Punkte
aufzunehmen.
Hierauf geht man zur Bestimmung des Zahlenwerthes der Größe n und endlich zur Ausführung der Zeichnung über.
Die Abmessung der einzelnen Linien der Zeichnung läßt sich am bequemsten mit einem in
Millimeter getheilten und mit Nonius versehenen Stangenzirkel bewerkstelligen.
Ausführung einer solchen Arbeit.
Fig. 36
stellt die erste und Fig. 37 die zweite
Projection eines auf diese Weise aufgenommenen Gegenstandes dar, beide mit Hülfe
eines solchen Instrumentes gemacht, dessen Ausführung ich Hrn. Inspector Meyerstein in Göttingen übertragen hatte. Für die
Berechnung der Coordinaten der bezeichneten Punkte hat man, wie aus unseren Formeln
zu ersehen ist, die Kenntniß folgender Zahlenwerthe nöthig:
x, y, y, x', y', n und v
oder, wenn man sich der größeren Genauigkeit wegen der
Formelgruppe (5) bedient:
x, y, z, a, a', n und v.
Durch die Messung dieser Größen ergab sich für n = 31570,
für v = 0. Bei der Messung von z ergab sich für beide Drehungsachsen ein Unterschied von 0,7 Millimetern,
nämlich
für die horizontale z'
=
320,32
z/z' = 1,0021
für die verticale z
=
321,02
In Folge dessen hätten die Zahlenwerthe des a und a' corrigirt werden müssen, da keine
Correctionsvorrichtung am Instrumente war; ich habe dieß jedoch der Einfachheit
wegen nicht gethan, wohl aber habe ich mich für die Berechnung der X des Zahlenwerthes von z
und für die Berechnung der Y des Zahlenwerthes z' bedient, wodurch der durch jene Ungleichheit bedingte
Fehler bis auf eine sehr kleine nicht mehr in Betracht kommende Größe wenigstens in
diesem, dem wichtigeren Theil der Rechnung, aufgehoben wird.
Der Augenpunkt ist in den Zeichnungen mit a und a' bezeichnet.
Zahlenwerthe der Größen
a
und a'
a
und a'
a₁ = 126,9
a'₁
= 48,3
a₁₄ =
165,8
a'₁₄ =
62,9
(33) 172,9
(33) 65,75
(15) 125,9
48,1
(5)
117,9
44,55
(12) 143,15
60,6
(2)
3,3
1,3
(18) 112,8
43,25
(31) 181,7
68,3
(19) 117,9
44,85
(32) 121,6
46,25
(3) 89,9
34,4
(7)
128,25
49,1
(16) 125,2
47,98
(9)
182,4
69,0
(17) 81,7
30,6
(10) 168,9
64,1
(11) 130,0
49,8
Zahlenwerthe der
x
und
y
x
n
y
n
n
n
(1)
+ 126,9
(2)
+ 3,3
(3)
– 89,9
(3)
+ 1,4
(5)
+ 2,2
(5)
+ 115,8
(7)
+ 1,4
(7)
+ 128,3
(9)
+ 128,6
(9)
+ 129,9
(10)
+ 108,7
(10)
+ 129,6
(11)
+ 20,9
(11)
+ 128,3
(12)
+ 55,5
(12)
+ 132,1
(14)
+ 108,85
(14)
+ 125,5
(15)
+ 20,9
(15)
+ 124,25
(16)
– 99,75
(16)
+ 78,2
(17)
+ 2,3
(17)
+ 81,8
(18)
+ 21,1
(18)
+ 110,9
(19)
+ 37,1
(19)
+ 110,9
(31)
+ 134,05
(31)
+ 122,9
(32)
– 2,7
(32)
+ 121,4
(33)
+ 127,2
(33)
+ 115,35
Berechnung der Werthe von
Z
n
n
=
1
33
5
2
31
33
7
log
a'
n
=
1,68395
1,81790
1,64885
0,11394
1,83442
1,66511
1,69108
log (an – a'n)
=
1,89542
2,02999
1,86540
0,30103
2,05461
1,87708
1,89845
log a'n/(an – a'n)
=
9,78853
9,78791
9,78345
9,81291
9,77981
9,78803
9,79263
log Z
n
=
4,28780
4,28718
4,28272
4,31218
4,27908
4,28730
4,29190
Z
n
=
19400
19372
19174
20520
19014
19378
19584
n =
9
10
11
14
15
12
18
19
1,83885
1,80686
1,69723
1,79865
1,68215
1,78247
1,63599
1,65176
2,05461
2,02036
1,90417
2,01242
1,89098
1,91672
1,84230
1,85824
9,78424
9,78650
9,79306
9,78623
9,79117
9,86575
9,79369
9,79352
4,28351
4,28577
4,29233
4,28550
4,29044
4,36502
4,29296
4,29279
Zn=
19209
19310
19604
19297
19518
23175
19633
19624
n =
3
16
17
1,53656
1,68106
1,48572
1,74429
1,88773
1,70842
9. 79227
9,79333
9,77730
4,29154
4,29260
4,27657
Zn =
19568
19616
18905
Berechnung der Werthe von
X
n
n
=
1
33
5
31
32
7
9
log Z/z
=
1,78127
1,78065
1,77619
1,77255
1,78077
1,78537
1,77698
log
x =
2,10346
2,10449
0,34242
2,12725
0,43136
0,14613
2,10924
log
X =
3,88473
3,88514
2,11861
3,89980
2,21213
1,93150
3,88622
Xn =
7669
7676
131
7940
163
85
7695
n =
10
11
14
15
12
18
1,77924
1,78580
1,77897
1,78391
1,85849
1,78643
2,03623
1,32015
2,03683
1,32015
1,74429
1,32428
3,81547
3,10595
3,81580
3,10406
3,60278
3,11071
Xn =
6538
1276
6543
1271
4007
1290
n =
19
3
16
17
1,78626
1,78501
1,78607
1,77004
1,56937
1. 95376
1,99891
0,36173
3,35563
3,73877
3,78498
2,13177
X
n
2268
5480
6095
13,54
Berechnung der Werthe von
Y
n
n
=
33
5
2
31
32
7
9
10
log Z/z
=
1,78159
1,77713
1,80659
1,77349
1,78171
1,78631
1,77792
1,78018
2,06202
2,06371
0,51851
2,08955
2,08422
2,10823
2,11361
2,11261
3,84361
3,84084
2,32510
3,86304
3,86593
3,89454
3,89153
3,89279
Yn =
6976
6932
211
7295
7344
7844
7790
7812
11
14
15
12
18
19
3
16
17
1,78674
1,78000
1,78485
1,85943
1,78737
1,78720
1,78595
1,78701
1,77098
2,10823
2,09864
2,09430
2,12090
2,04493
2,04493
0,14613
1,89321
1,91276
3,89497
3,87864
3,87915
3,98033
3,83230
3,83213
1,93208
3,68022
3,68373
7852
7562
7571
9557
6797
6794
85,5
4789
4828
Zusammenstellung der durch die Rechnung gewonnenen
Resultate.
n
X
n
Y
n
Z
n
1
+ 7669
+ 0
19400
33
+ 7676
+ 6976
19372
5
+ 131
+ 6932
19174
31
+ 7940
+ 7295
19014
32
– 163
+ 7344
19378
7
+ 85
+ 7844
19584
9
+ 7695
+ 7790
19209
10
+ 6538
+ 7812
19310
11
+ 1276
+ 7852
19604
14
+ 6543
+ 7562
19297
15
+ 1271
+ 7571
19518
12
+ 4007
+ 9557
23175
18
+ 1290
+ 6797
19633
19
+ 2268
+ 6794
19624
3
– 5480
– 85,5
19568
16
– 6095
+ 4789
19616
17
+ 1354
+ 4828
18905
2
0
+ 211
20520
Wollte man wissen, mit welcher Schärfe diese gefundenen Dimensionen mit der
Wirklichkeit übereinstimmen, so müßte man alle diese einzelnen Theile des Gebäudes
auf directem Wege nachmessen, allein dieß ist eine sehr umständliche Arbeit, da man
nicht ohne Weiteres zu den einzelnen Theilen gelangen kann, außerdem genügen auch
schon folgende einfache Betrachtungen, um sich ein Urtheil über die Genauigkeit
dieser Bestimmung zu bilden.
Es ist einleuchtend, daß wenn man eine bis zu einem gewissen Grade gehende Symmetrie
in den einzelnen Theilen des Gebäudes voraussetzt, die Differenzen der X für gewisse Punkte dieselben oder nahezu dieselben
seyn müssen, wie z.B.
X
₉– X₁₀ = 1157
X₁₁ – X₇ = 1151
6
X₃₃ –
X₀ = 7676
X₁ – X₀ = 7669
3
X₁₄ – X₁₅ = 5272
X₁₀ – X₁₁ = 5262
10
X₁₉ –
X₁₈ = 978direct gemessen
= 980
2
Woraus sich, wie man sieht, für die größte Differenz 10 Millimeter auf 5272, also
noch nicht einmal 1/4 Procent ergibt.
Ebenso ergibt sich für
Y₁₁ = 7852
Y₇ = 7844
8
Y₁₀ = 7812
Y₉ = 7790
22
Y₁₅ = 7571
Y₁₄ = 7562
9
Y₃₂ = 7344
Y₃₁ = 7295
49
X₃₃ = 6976
Y₅ = 6932
44
Y₁₁ = 7852
Y₁₀ = 7812
40
Y₁₈ = 6797
Y₁₉ = 6794
Aus dieser Zusammenstellung ergibt sich, daß das Haus nach der linken Seite hin, in
der Nähe der y Achse, etwas höher ist, als nach der
andern Seite hin, im Uebrigen harmoniren diese Zahlen so gut als man es nur irgend
verlangen kann. Wenn man bedenkt, daß ein hölzernes Haus, welches schon etwa 11
Jahre hindurch Wind und Wetter preisgegeben ist, unmöglich nach dieser Zeit, wenn es
auch ursprünglich im besten Zustand war, nach den Regeln der Symmetrie vollkommen
entsprechen kann, wie man z.B. aus Y₃ = –
85 ersieht, so hat man allen Grund, die Leistungen des Instrumentes sehr
befriedigend zu nennen.
Gotha, 20. December 1852.
Tafeln