| Titel: | Ueber die saccharometrische Bierprobe. |
| Autor: | Dr. Prof. Karl August Steinheil [GND] |
| Fundstelle: | Band 101, Jahrgang 1846, Nr. X., S. 34 |
| Download: | XML |
X.
Ueber die saccharometrische
Bierprobe.
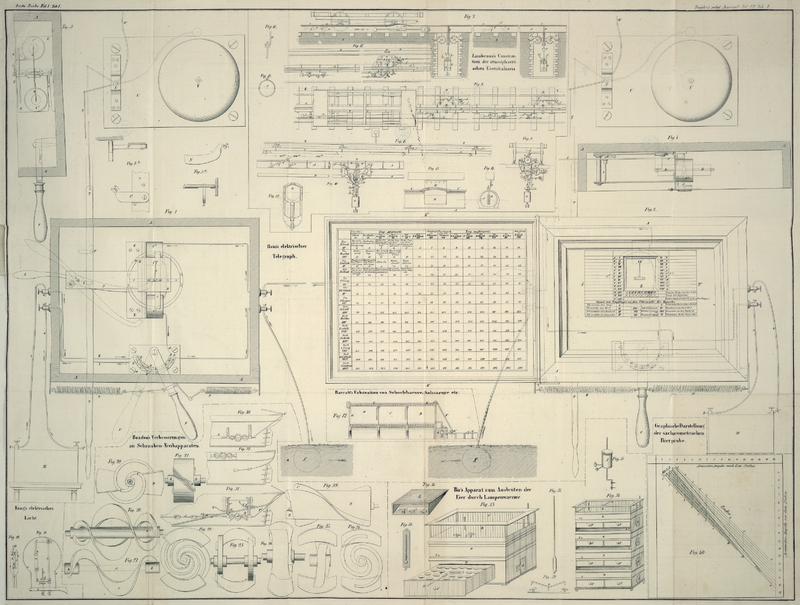
Mit einer Abbildung auf Tab. I.
Steinheil, über die saccharometrische
Bierprobe.
Das bayerische Kunst- und Gewerbeblatt, Maiheft 1846,
enthält S. 275–286 eine Abhandlung von Hrn. Professor Steinheil in München, worin er die
sogenannte saccharometrische Bierprobe des Hrn. Prof. Balling in Prag beleuchtet, folgenden
wesentlichen Inhalts:
„Hr. Prof. Balling in Prag
empfiehlt unter dem Namen der saccharometrischen Bierprobe
seine Methode und seine Vorschriften zur Untersuchung der
Biere in dessen Buch „die Bierbrauerei
1845“ auf das nachdrücklichste, indem er S.
439 als erwiesen betrachtet, daß alle
bisher erfundenen Bierprüfungsmethoden ungenügend
sind, und daß nur die saccharometrische Probe
wirklich ganz entspreche. Dieselbe beruht auf zwei
Beobachtungen des specifischen Gewichts des Biers mit dem
Aräometer, 1) im ungeänderten Zustande desselben, 2) nach
Entfernen des Alkohols durch Einsieden, worauf das
ursprüngliche Gewicht durch Wasser wieder ersetzt wird. Da
nun das Aräometer bei der zweiten Beobachtung nur die
wässerige Lösung des Extracts zu messen hat und dieser wohl
als Zucker betrachtet werden kann, so hat der Erfinder diese
Probe die saccharometrische genannt.
Ich muß gestehen daß ich nicht einsehe, was Hr. Balling durch diese seine Methode
eigentlich gewinnen will im Verhältniß zu der längst
bekannten chemischen Trennung von Zucker und Alkohol. Denn
der größte Zeitaufwand wird erfordert, um den Alkohol völlig
zu entfernen. Ist aber dieß einmal geschehen, so brauchen
wir doch wohl keine besondere Methode, um zu finden, wie
viel Zucker in einer bloß zuckerhaltigen Lösung und wie viel
Alkohol in einem Weingeist enthalten ist. Für beides haben
wir sehr genaue Tabellen und Vorschriften in jedem Lehrbuche
der Chemie. Kennt man aber einmal den Zucker- und den
Alkoholgehalt nach Procenten einer Biersorte, so läßt sich
daraus berechnen, wie viel Extract in der Würze enthalten
war, wie viel Eimer Bier vom Scheffel Malz bei bestimmten
Annahmen gewonnen worden sind,Siehe meine Abhandlung „über quantitative
Analyse durch physikalische Beobachtungen im
polytechn. Journal Bd. LXXXVIII S. 285.
kurz alles, was vom Zucker- und Alkoholgehalt
einer Flüssigkeit abhängt. Da aber nun Hr. Balling von dieser Methode
abgeht, die er selbst die allerbeste nennt (S. 428), so muß
er doch wohl seine guten Gründe dazu haben. Gewinnt er an
Zeit, die für den Versuch erforderlich ist? Ja, denn er
braucht den Alkohol nicht in einer Vorlage aufzufangen...
deren Inhalt nicht erst wieder auf das ursprüngliche Gewicht
mit Wasser zu ergänzen, sondern er berechnet den Alkohol aus
der zweiten Beobachtung aus dem bloß zuckerhaltigen
ergänzten Rückstand. Wäre die Rechnung daher leicht und
einfach, so könnte von dieser Seite wenigstens ein kleiner
Zeitgewinn zu erwarten seyn. Das ist sie aber durchaus
nicht; denn sie fordert, daß man
1) mit den zwei Beobachtungen aus der Tafel I. nehme m und n;
2) findet sich d = n – m, dieß gibt
3) den genäherten Werth von A =
(n – m) c, wo mit c multiplicirt
werden muß;
4) 2 A + n ist ein genäherter Werth von p;
5) mit e wird q und b aus Tafeln genommen. Damit rechnet man
6) p = (nq
– m)/(q –
1). Nun ist endlich
7) das wahre A = (p – n) b
zu berechnen.
Alle diese Rechnung wendet Hr. Balling nur an, um den Alkohol und den Extract der
Würze zu finden. Kann dieß einfach genannt werden?
Uebrigens muß hier bemerkt werden, daß diese Weitläufigkeit
nicht etwa in der Aufgabe liegt, welche sich Hr. Balling gestellt hat. Man hätte
die Tafel so einrichten können, daß man aus den zwei Angaben
der Saccharometer unmittelbar den
Alkohol und Extract der Würze
gefunden hätte. Statt dessen bringt Hr. B. für nichts und
wieder nichts 7 Größen unnöthig in die Rechnung.
Da nun von dieser Seite nichts gewonnen ist, wollen wir
sehen, ob vielleicht die Methode, den Alkohol aus seinem
Verschwinden zu bestimmen, größere Genauigkeit gibt, als
wenn er in der Vorlage aus dem zum ursprünglichen Gewicht
ergänzten Weingeist bestimmt worden wäre.
Es ist klar, daß eine Alkoholspindel in diesem Weingeiste
direct den Procentgehalt angibt (wenn die Temperatur die
normale), daß also ein Fehler in der Ablesung der Spindel
von 1/10 Proc. oder Grad einen eben so großen Fehler in dem
Erkennen des Alkoholgehalts hervorbringen würde. Wenn man
aber nun untersucht, wie groß der Fehler ist, der in dem
Auffinden des Procentgehalts des Alkohols begangen wird nach der saccharometrischen Probe unter der Annahme,
daß auch an dem Saccharometer 1/10 Grad in der Ablesung
gefehlt sey, so findet man 1/4 Proc. des Alkohols. D.h. wenn
der ganze Alkoholgehalt des Biers 2 Gewichts-Procente
betrug, so ist der Fehler in der Bestimmung des Alkohols 1/8
der ganzen Quantität! Da nun aber sehr nahe die doppelte
Menge des Alkohols Extract war, aus welchem er sich gebildet
hat, so ist seine Bestimmung des ursprünglichen Würzgehalts
eines Biers um das Doppelte unsicher, d.h. unsicher auf 1/2
Proc. Malzzucker, wenn in der Ablesung des Saccharometers
1/10 Grad gefehlt wurde. Diese Unsicherheit liegt in der
Natur der Aufgabe. Aber Hr. B. hat eine zweite Unsicherheit
bloß durch die Form seiner Rechnung wahrhaft künstlich
hineingebracht.
Er dividirt nämlich zur Bestimmung des Werths von p mit q – 1; q ist
aber circa 1.25, also q –
1 nur 1/4, wodurch nun der Fehler in m circa 4mal, der Fehler in n 5mal vergrößert wird. Um dieß ganz anschaulich
zu machen, werde ich das Beispiel aufgreifen, welches Hr.
Balling in seinem Werke S.
443 beginnt und auch in seiner Brochüre: Saccharometer etc.
S. 69 wieder abdruckt.
Dort ist m = 4.250, n = 5.550 angenommen, was gibt
p = 11. 177.
Allein S. 12 und 84 der Brochüre ist ausdrücklich gesagt, daß
die Ablesung von 1/10 Grad am Saccharometer ausreichend sey
für alle die in Praxi vorkommenden Fälle. 1/10 Grad ist
daher als ein statuirter Fehler betrachtet.
Eben so ist S. 60 der Brochüre bemerkt, daß q bis auf 0 . 003 fehlerhaft
seyn könne.
Demgemäß nehmen wir nun einen Fehler in m und n von 1/10 Grad, in q
von 0.0027 an und setzen m =
4.350; n = 5.450, so wird q = 1.2327 und nach den Tafeln
des Hrn. Balling
p = 10.177; früher fanden
wir
p = 11.177.
Hier beträgt also der Fehler in der Bestimmung des
Gesammtgehalts sogar ein Procent,
d.h. 1/11 des Gesammtgehalts, wenn bei der Beobachtung der
Saccharometer nur 1/10 Grad irrig
abgelesen worden, was Hr. Balling
selbst als ausreichend bezeichnet.
Um keinen Zweifel über die Richtigkeit dieser allerdings sehr
überraschenden Angabe zu lassen, wollen wir zur Controle der
Rechnung nach der Tafel den Ausdruck von p in Bezug auf m, n und q differenciren. Dieß gibt
dp = dn.
q/(q – 1)
– dm./(q – 1) – (n – m)/(q – 1)² dq.
Setzen wir wie oben
=
dm = + 0.1
dn
= – 0.1
dq = + 0.0027
wobei wie im durchgeführten Beispiele
m =
4.250; n =
5.550; q = 1.230
so ergibt sich
dp =
– 0.432 ... (dn q/(q – 1))
– 0.511 ... (–
dm/(p – 1))
– 0.057 ... (–
dq (n – m)/(q –
1)²)
–––––––––––––––
also dp =
– 1.000
übereinstimmend mit der directen Rechnung nach der Tafel.
Ein Procent ist bei 11 Procent Gesammtgehalt also der
mögliche Fehler nach der Methode des Hrn. Balling. Der mittlere Fehler
einer Bestimmung wird jedoch kleiner seyn. Aber nehmen wir
selbst an, er betrage nicht mehr als 0.025 eines Grads am
Saccharometer, was jedenfalls die äußerste Gränze ist, so
wird doch der Extractgehalt der Würze nur auf 1/4 Proc. oder
etwa 1/40 des Ganzen bestimmt. Derselbe Fehler von 1/40 wird
erzeugt nicht bloß durch unvermeidliche Unsicherheit in der
Ablesung der Aräometer, sondern auch dadurch, daß die
Temperatur nur 3/4⁰ von der normalen abweicht. Solche
Abweichungen sind aber gar nicht zu vermeiden, wenn die
Lufttemperatur weit abliegt von der normalen. Aber diese
Quelle von Fehlern wird ihren vollen Einfluß üben eben so
auf das 1000 Gran Fläschchen, wie auf die Aräometer. Durch
Anwendung des Fläschchens, was Hr. Balling in neuester Zeit eingeführt, wird also ein
Fehler dieser Größe auch nicht zu entfernen seyn.
Um so auffallender muß es erscheinen, wenn Hr. Balling S. 438
seines Werks aus Zahlen nachweisen will, daß die
hallymetrische Probe unzureichend sey, weil durch die
Annahme von Prof. Kaiser sich der
Gehalt eines Biers 12.2 finden würde, während er 12.0 ist.
Hier beträgt der Fehler nach der Kaiser'schen Annahme 1/60 des Ganzen. Deßhalb also
verwirft Hr. Balling die
hallymetrische Probe, weil sie 1/60 fehlt, und nennt dagegen
seine saccharometrische die einzig brauchbare, während
Fehler von 1/40, wie ich gezeigt habe, bei ihr ganz
unvermeidlich sind.
Wir sehen also, daß die saccharometrische Probe nicht nur
durch ungeeignete Anordnung der Rechnung und Tafeln sehr
weitläufig und unbequem, sondern auch viel ungenauer ist,
als die directe Bestimmung des Alkohols. Ein Theil dieser
bedeutenden Unsicherheit liegt darin, daß Hr. Balling einen ungünstigeren Fall
der Trennung von Zucker und Alkohol aus Beobachtungen zur
Grundlage seiner Methode gemacht hat, als wenn er bei der
bekannten chemischen Ausscheidung geblieben wäre. Ein
anderer Theil der Unsicherheit ist aber rein ohne alle Noth
von ihm in die Lösung der Aufgabe hineingebracht worden, wie
wir schon umständlich nachgewiesen haben. Um dieß noch
anschaulicher zu machen, sogar für solche, die gar nichts
von Rechnung verstehen, habe ich die Aufgabe des Hrn. Balling geometrisch
construirt.
Fig.
40 zeigt den Zusammenhang der Ablesungen beider
Aräometer vor und nach dem Sieden mit den Gehalten an
Alkohol und Extract der Würze. Die Linien, auf welchen
Alkohol und Extract der Würze constante Werthe haben, führen
zu den Scalen, welche den entsprechenden Procentgehalt
angeben. Hier ist nun gleich ersichtlich, daß die Ablesung
des Aräometers vor dem Sieden
einen sehr großen Einfluß auf die Bestimmung des Alkohols
ausübt und 4 3/4mal genauer seyn müßte, als die Angabe des
Saccharometers nach dem Sieden, um den Alkohol ebenso genau
erkennen zu lassen als den Zucker. Man betrachte nur, unter
welchen spitzen Winkeln sich die Alkohol- und
Würzgehaltscurven schneiden, und man wird sich überzeugen,
wie ungünstig der Fall gewählt ist zu ihrer Bestimmung. Die
durch die Tafeln von Hrn. Balling
hineingebrachte Unsicherheit ist hier in der Construction
verschwunden. Die Construction ist also doch gewiß besser
als die Tafel, denn sie zeigt, daß die Aufgabe ungeschickt
gewählt ist, und nie, auch abgesehen von dem großen
Zeitaufwand, praktisch brauchbar gelöst werden kann.
Allein Hr. Balling ist sogar der
Meinung, daß die saccharometrische Probe mehr leiste, als
jede andere, und daß nur sie alles das beantworte, was man
von dem untersuchten Bier zu wissen wünscht. Er verlangt,
daß eine Bierprobe beantworte:
1) Wie viel absoluter Alkohol und Zucker sind in 100 Gran des
Biers?
2) Wie groß war der Extractgehalt der Würze in
Gewichtsprocenten, woraus das Bier erzeugt wurde?
3) Welche Schüttung an Gerstendarrmalz wurde zur Erzeugung
dieser Würze angewendet?
4) Welches ist der Vergährungsgrad dieses Biers?
Darin sieht nun Hr. Balling den
wesentlichen Vortheil seiner saccharometrischen Probe vor
der hallymetrischen (S. 437) und vor der
optisch-aräometrischen (S. 439), daß durch die
letztern aus zwei Beobachtungen nur etwa der Zucker-
und Alkoholgehalt bestimmt werden kann, nach seiner Probe
aber die vier oben gestellten Fragen beantwortet werden.
Offenbar ist Hr. Balling hier
wieder im Irrthum begriffen. Jede der benannten Bierproben
bestimmt nur zwei Unbekannte. Aber wenn diese bekannt
geworden sind, dann lassen sich aus ihnen noch anderweitige
Functionen mit Zuziehung weiterer Betrachtungen ableiten.
Aus keiner jedoch mehr und keiner weniger, als aus der
andern. So leicht dieß zu begreifen scheint, so muß es doch
Hrn. Balling entgangen seyn. Es
ist dieß um so auffallender, als Hr. Balling auch aus meiner Abhandlung über
quantitative Analyse hätte ersehen können, daß ich schon
1843 diese Fragen beantwortet habe. Denn dort ist nicht nur
aus dem Zucker und Alkohol sämmtlicher Münchener Winterbiere
der Extractgehalt der ursprünglichen Würze in
Gewichtsprocenten berechnet, sondern auch die Gußführung mit
den von Prechtl gegebenen
Constanten angeführt. Auch der Zusammenhang zwischen
Malzzuckergehalt in der Würze und der Anzahl Eimer Bier per Scheffel Malz findet sich
verglichen mit dem Biertarif von 1811. Endlich ist das
Fortschreiten der Alkoholbildung auf Kosten des Zuckers
erörtert. Sind daher die vier obigen Fragen erst jetzt von
Hrn. Balling beantwortet?
Man sieht also doch wohl hieraus, daß die Einwendungen,
welche Hr. Balling gegen die
andern Bierproben macht, eben so wenig begründet sind, als
die Vortheile, welche er seiner Probe zueignen möchte.
Denn der mittlere Fehler einer Ablesung der optischen Probe
abgeleitet aus 92 Beobachtungen verschiedener Beobachter
beträgt
± 0.315 Trommeltheile.
Ebenso der mittlere Fehler einer Senkspindelablesung
+ 0.03 Grade.
Hieraus findet sich nun durch Anwendung einer Reductionstafel
ähnlich construirt, wie die von mir im polytechnisches
Journal Bd. XCIX S. 363 beschriebene, in welcher der
ursprüngliche Malzzuckergehalt der Würze und der Grad der
Alkoholbildung als Curven eingetragen sind, die unmittelbar
mit den zwei Ablesungen der Instrumente zusammenhängen, der
mittlere Fehler der einmaligen Bestimmung
für
Optisch
Aräometrisch
Summe der
Fehler in
Procenten
Mittlere Fehler
in
Procenten
Zucker
0,30
0,03
0,06
0,04
Alkohol
0,043
0,043
0,09
0,058
Würze
0,10
0,027
0,13
0,04
Alkoholbildung
0,002
0,003
0,005
0,0036
Bei Anwendung der saccharometrischen Probe ist der mittlere
Fehler circa 3mal größer als
hier.
Wenn aber auch die saccharometrische Probe eben so genau wäre
als die optisch-aräometrische, wenn es auch eben so
bequem wäre, alle Rechnungen nach Hrn. Balling's Angaben und Tafeln zu führen, als ohne
alle Rechnung nur das Resultat an der Schubtafel abzulesen,
wie es bei der optisch-aräometrischen der Fall ist,
so scheint doch der optisch-aräometrischen Probe noch
dadurch ein kleiner Vorzug zuzukommen, daß die vollständige
Untersuchung einer Biersorte mit Ableitung aller Resultate
nicht ganz 3 Minuten Zeit fordert,Im Mittel aus 92 untersuchten Vieren, wobei alle
Ablesungen doppelt und zwar von zwei Beobachtern
gemacht sind. während bloß die Experimente nach der
saccharometrischen Probe, wie Hr. Balling selbst anführt, 2 Stunden Zeit
erfordern!
Fassen wir nochmals das Gesagte kurz zusammen, so haben wir
nachgewiesen:
daß die Alkoholbestimmung aus der specifischen
Gewichtsabnahme nach Entfernen des Alkohols eine
Unsicherheit von 1/4 Proc., also in der Extractbestimmung
der Würze von 1/2 Proc. läßt; daß diese Unsicherheit durch
die Einrichtung der Tafeln unnöthig vergrößert wird bis zu 1
Proc. im Würzegehalt oder 1/10 des Ganzen; daß auch mit
allen möglichen Cautelen der mittlere Fehler nicht unter
1/4, Proc. zu bringen ist, daher die Probe nicht die von der
Praxis verlangte Genauigkeit besitzt; daß dieses Resultat
nur durch eine sehr weitläufige Rechnung gewonnen wird,
während es bloß durch Addition von 2 Zahlen, wie bei der
optisch-aräometrischen Probe, hätte erlangt werden
können, oder auch ganz ohne Rechnung gegeben werden kann,
wie die Figur nachweiset; daß der Vorwurf, es
gebe die hallymetrische Probe unrichtige Resultate, nur
darauf gegründet ist, daß sie 1/60 fehlt, während die
saccharometrische 1/10 fehlen kann; daß aus der
saccharometrischen Probe nicht mehr gefolgert und abgeleitet
werden kann, als aus jeder andern Bierprobe, die Zucker und
Alkohol bestimmt; daß bei der optisch-aräometrischen
Probe alle diese Bestimmungen ganz ohne Rechnung gemacht
werden und direct durch die Ablesungen beider Instrumente
gegeben sind; daß der mittlere Fehler in der
Würzextractbestimmung hier kein Zehntel Proc., d. i. kein
Hundertstel des Gehalts beträgt, während er bei dem
Saccharometer aber circa 4mal
größer ist; daß die Saccharometerprobe immer unpraktisch
bleiben wird, auch abgesehen von ihrer Ungenauigkeit,
dadurch, daß 2 Stunden Zeit bloß zu den Experimenten
erforderlich sind, während bei der
optisch-aräometrischen Probe zur ganzen Analyse 3
Minuten genügen; daß daher diese zwei Proben gar nicht mit
einander verglichen werden können, weil die eine, die
optisch-aräometrische, allen billigen Anforderungen,
die andere keiner entspricht.“
Tafeln