| Titel: | Ueber die Wirkungen der Eisenbahnkrümmungen, von Edward Sang Esq., Civilingenieur in Edinburg. |
| Fundstelle: | Band 79, Jahrgang 1841, Nr. LXVIII., S. 342 |
| Download: | XML |
LXVIII.
Ueber die Wirkungen der
Eisenbahnkruͤmmungen, von Edward
Sang Esq., Civilingenieur in Edinburg.
Aus Jameson's Philosoph. Journal. Jan. 1841, S.
334.
Mit Abbildungen auf Tab.
V.
Sang, uͤber die Wirkungen der
Eisenbahnkruͤmmungen.
Die ungeheure Geschwindigkeit, welche man neuerdings auf Eisenbahnen erreicht hat,
bringt alle Mängel ihrer Construction auf eine unverkennbare Weise zum Vorschein,
und sezt das Publicum in die Notwendigkeit, jede Minute eines Unfalls gewärtig zu
seyn. Es ist bekannt, daß ein Eisenbahnzug, wenn er sich auf einer Krümmung
fortbewegt, das Bestreben äußert, die Schienen zu verlassen und in geradliniger
Bewegung zu verharren. Um den üblen Folgen dieses Bestrebens vorzubeugen, legt man
die äußere Schiene um so viel höher, daß die quer durch die Schienen gezogene Linie
senkrecht zu der
Resultante der Schwerkraft und Centrifugalkraft steht. Diese Vorsichtsmaßregel
beseitigt gänzlich jede Neigung der Waggons von den Schienen zu weichen, und jeden
Druk gegen die Achsenenden. Der Punkt aber, auf welchen ich die Aufmerksamkeit der
Societät hinzulenken wünschte, betrifft den Uebergang des Trains von der geraden
Linie in eine Curve, oder von einer Curve in eine andere.
Einige betrachten es als genügend, daß der gerade Theil der Schienenleitung tangent
an den Kreis sey, welcher die Krümmung bildet, oder daß die kreisförmigen Theile der
Bahn an ihrer Vereinigungsstelle eine gemeinschaftliche Tangente besizen. Diese
Vorkehrung beseitigt zwar jede plözliche Biegung, entspricht aber bei weitem noch
nicht den Bedürfnissen einer im Betrieb befindlichen Eisenbahn.
Um dem hier angedeuteten Mangel auf den Grund zu kommen, folge man einem Waggon in
seinem Lauf von der einen nach der anderen Richtung. In dem Augenblik, wo er die
gerade Linie verläßt, und in den Kreisbogen übergeht, tritt die Centrifugalkraft in
Thätigkeit; es muß daher für eine Erhöhung der äußeren oder eine Depression der
inneren Schiene gesorgt seyn. Die Passagiere, in ihrem unwillkürlichen Bestreben in
der geradlinigen Bewegung zu verharren, empfinden einen sanften, aber doch
plözlichen Druk nach der einen Seite des Wagens. Da die Erhebung der Schiene nicht
plözlich seyn darf, so ist vor oder hinter dem Uebergangspunkt der Krümmung eine
besondere Anordnung nöthig. Diese darf nie fehlen, wo ein schneller Uebergang von
einem Grade der Krümmung in einen andern stattfindet.
Es dringt sich daher von selbst die Frage auf, wie dürfte wohl die Krümmung der
Eisenbahnen beschaffen seyn?
Eines ist gewiß, daß der Uebergang der Krümmung nie ein abrupter seyn darf, und daß
die Vereinigung kreisförmiger Bögen unzulässig ist.
Betrachtet man die längs der Schiene gemessene Distanz als Abscisse, so kann die
Krümmung als eine Function dieser Distanz angesehen werden; und diese Function muß
von solcher Beschaffenheit seyn, daß die Krümmung an dem Punkte, wo die Abweichung
von der geraden Linie anfängt, gleich Null ist. Sezt man die von diesem Punkte aus
berechnete Länge = l, und bezeichnet die Krümmung mit
ρ, so ist die einfachste Function, welche
dieser Bedingung genügt:
ρ = nl
d.h. die Krümmung ist dem Abstände von dem genannten Punkte
proportional. Diese Function ist indessen für den vorliegenden Zwek unzureichend,
weil sie eine beständige Zunahme der Krümmung geben würde, während doch der
Hauptzwek einer Eisenbahncurve darauf hinzielt, um von einer Richtung nach einer
andern zu schaffen – zwei gerade Theile der Bahnlinie mit einander zu
verbinden. Deßwegen muß die Krümmung bis zu einem Maximum zunehmen, dann aber
abnehmen, bis sie an der Stelle, wo sie an den zweiten geraden Theil stößt, gleich
Null wird. Die einfachste Function, welche die verlangte, so eben bezeichnete
Eigenschaft besizt, ist:
ρ = nl (L – l)
wo L die ganze Länge von dem einen
geraden Theil bis zum andern bezeichnet. Eine Curve, welcher diese charakteristische
Eigenschaft zukommt, ist von dem Fehler, worauf ich hindeutete, ganz frei; und doch
ist sie, wenn man genauer untersucht, nicht ganz frei von Fehlern, indem die
verticale Projection der äußeren Schiene, wenn man sie in eine gerade Linie sich
gestrekt denkt, parabolisch ist.
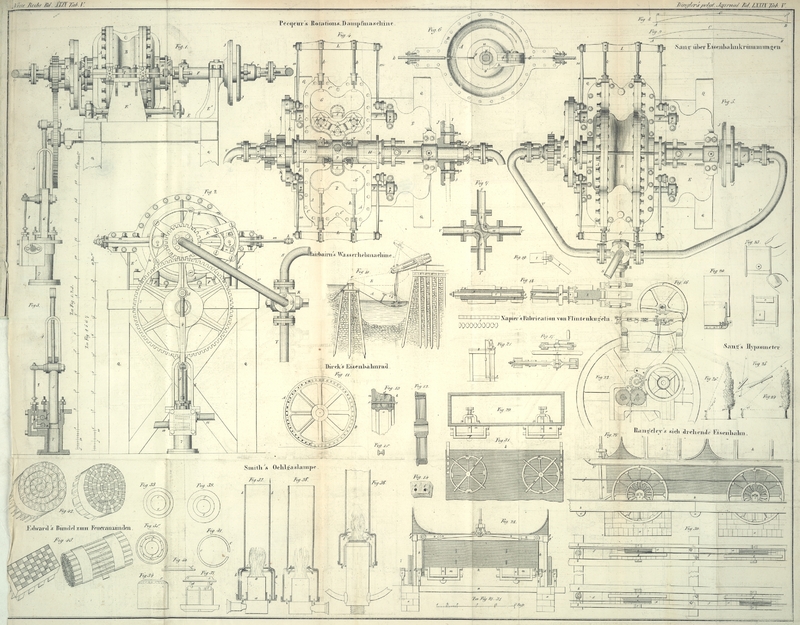
A und B, Fig. 8, seyen die beiden
Endpunkte der Krümmung, und AB die Oberfläche der
inneren Schiene, so würde die Parabel ABC die
Oberfläche der äußeren Schiene vorstellen; für die Annahme einer kreisförmigen
Ausbiegung würde sie durch die Linie αβ, und zwar in jedem Ende plözlich abgebrochen dargestellt
seyn. Die Curve ABC ist unzweifelhaft der Linie
AαβB, welche in der Wirklichkeit
nie angenommen werden kann, vorzuziehen; aber nichtsdestoweniger muß sie in den
Punkten A und B einen
Widerstand resultiren, welcher mit dem Quadrate der Geschwindigkeit zunimmt. An den
beiden Uebergangspunkten A und B der Curve in die gerade Linie sollte die Curve etwa die Form wie in Fig. 9
haben.
Ich will nun die stufenweisen Fortschritte der Verbesserungen, auf welche ich
hindeutete, näher beleuchten. Wir haben zuerst die Function ρ = 1/r (constant), deren erste
Ableitung gleich Null ist. Zweitens ρ = nl, wovon die zweite Ableitung gleich Null ist;
drittens ρ = nl
(L – l), wovon
die dritte Ableitung gleich Null ist. Die Wirkung wird mit der Anzahl der
Ableitungen sanfter. Zum Behuf weiterer Verbesserung muß man eine Function noch
höherer Ordnung nehmen. Angenommen nun, diese Functionen lassen sich vollständig in
Factoren auflösen, so wirb die durch sie dargestellte Curve so viele Flexionspunkte
besizen, als die Function Dimensionen besizt, sie wird daher ein wellenförmiges
Aussehen haben. Für diejenigen, welche mit der höheren Analysis vertraut sind,
bedarf es kaum der Erwähnung, in wie weit die vollständige Erforschung solcher
Curven die gegenwärtigen Kräfte dieser mächtigen Wissenschaft übersteigt; sie werden
sogleich in der Curve der Sinus eine transscendente Function erkennen, welche eine
unbegränzte Reihe von Ableitungen besizt und deren Form, dem Calcül leicht zugänglich, alles
das Wesentliche umfaßt, was wir suchen.
Ich nehme daher als die für die Verbindung zweier gerader Theile einer Eisenbahn
geeignete Krümmung denjenigen Theil der Curve der Sinus an, welcher auf einer Seite
ihrer Achse enthalten ist.
Tafeln