| Titel: | Berechnung des dynamischen Effectes des durch Expansion wirkenden Dampfes. Von Gustav Bernoulli in Basel. |
| Autor: | Gustav Bernoulli [GND] |
| Fundstelle: | Band 47, Jahrgang 1832, Nr. LXXIII., S. 401 |
| Download: | XML |
LXXIII.
Berechnung des dynamischen Effectes des durch
Expansion wirkenden Dampfes. Von Gustav
Bernoulli in Basel.
Mit Abbildungen auf Tab.
VI.
Bernoulli, Berechnung des dynamischen Effectes durch
Expansion.
Bei den Maschinen, welche ohne Expansion arbeiten, tritt der Dampf
fortwaͤhrend bald von Oben, bald von Unten in den Dampfcylinder ein, und es
braucht daher, um einen einfachen Kolbenzug zu bewirken, ein Volumen Dampfes,
welches gleich ist dem Volumen eines Cylinders, dessen Basis diejenige des
Dampfcylinders und dessen Hoͤhe die Kolbenhubshoͤhe ist.
Bei den Expansionsmaschinen hingegen fuͤllt der Dampf bei jedem Kolbenzuge nur
eine Portion des Dampfcylinders aus, und es wird alsdann die Communication des
Cylinders und des Dampfkessels durch irgend eine Vorrichtung unterbrochen, welche
jedoch den Ausgang des Dampfes, dessen Wirkung bereits vollendet ist, aus dem
Dampfcylinder fortwaͤhrend gestattet. Der Dampf wirkt also nur
waͤhrend eines gewissen Theiles der Zeit, welche der Kolben braucht, um die
ganze Hubslaͤnge zu durchstreichen, mit seiner anfaͤnglichen Pression,
dehnt sich aber dann vermoͤge seiner expandirenden Kraft aus, und
fuͤllt zulezt den ganzen Dampfcylinder an. Waͤhrend dieß geschieht,
wirkt derselbe noch fortwaͤhrend auf den Kolben, jedoch mit einer Pression,
welche sich mit der Zunahme seines Volumens immer mehr und mehr vermindert.
Bei Maschinen, welche mit zwei Dampfcylindern versehen sind, wirkt der Dampf in einem
derselben bestaͤndig mit seiner anfaͤnglichen Pression, tritt aber,
nachdem er den Kolben desselben die ganze Hubslaͤnge hindurch getrieben hat,
in einen zweiten viel groͤßeren Cylinder, wo er sich ausdehnt, und noch mit
einer immer abnehmenden Pression auf den darin befindlichen Kolben wirkt.
Indem man eine gewisse Quantitaͤt Dampfes auf diese oder jene Weise durch
Expansion wirken laͤßt, kann man hiemit den Effect derselben bedeutend
vergroͤßern, was aus folgenden Berechnungen derselben deutlich ersehen werden
kann.
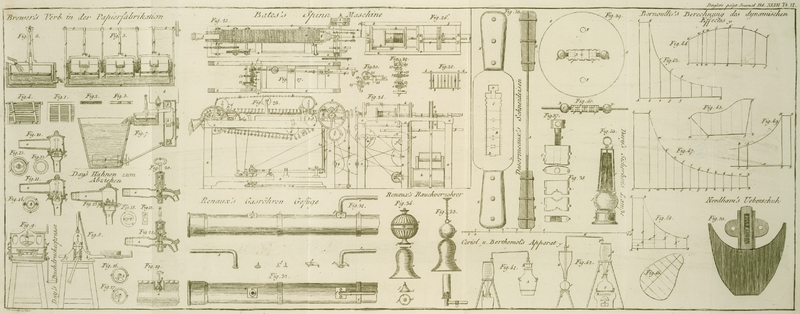
Es sey AB (Fig. 43) die
Laͤnge des Dampfcylinders, oder vielmehr die Hubslaͤnge des Kolbens,
und es werde die Pression des hineinstroͤmenden Dampfes durch die Linie AC ausgedruͤkt. Laͤßt man nun Dampf
in den Cylinder einstroͤmen, doch nur von A bis
d, und schließt alsdann die Communication der
Dampfroͤhre mit dem Cylinder, so wird dieser Dampf, waͤhrend er den
Kolben von A nach d treibt,
einen dynamischen Effect hervorbringen, der durch den Flaͤcheninhalt des
Parallelogrammes Add'C ausgedruͤkt werden
kann, und daher = Ad × AC ist.
Laͤßt man nun diesen Dampf, ohne eine neue Quantitaͤt
hineinstroͤmen zu lassen, noch fernerhin auf den Kolben wirken, so wird
derselbe in dem Punkte e, wenn Ad = de ist, nur
noch eine halb so große Pression besizen, da sein Volumen das Doppelte geworden ist,
und dieselbe hiemit durch ee' = 1/2 AC ausgedruͤkt werden. Der dynamische
Effect, welchen er auf den Kolben ausuͤbt, waͤhrend der, selbe von d bis e gestoßen wird, kann
daher durch den Inhalt der trapezfoͤrmigen Figur dd'e'e bezeichnet werden. Eben so wird der Dampf durch dreifache
Expansion, d.h. indem er ein drei Mal so großes Volumen einnimmt, als sein
anfaͤngliches war, auf den Kolben, waͤhrend derselbe von e nach f fortschreitet (wenn
ef = Ad),
einen dynamischen Effect hervorbringen, der dem Inhalte der Figur ee'ff' gleichgesezt werden kann, deren Seite ff' = 1/3 AC
ist, und der totale dynamische Effect dieser Quantitaͤt Dampfes durch
dreifache Expansion durch den Inhalt der Figur ACd'e'f'fA ausgedruͤkt werden.
Es fraͤgt sich daher zuerst, wie der Inhalt einer solchen Figur, deren eine
Seite Cd'e'f' aus einer krummen Linie besteht,
berechnet werden kann.Da dieses von Hrn. Poncelet angegebene
approximative Verfahren in allen Faͤllen mit Vortheil angewendet
werden kann, wo man den Flaͤcheninhalt einer von Curven
eingeschlossenen Figur zu berechnen hat, und da dasselbe meines Wissens noch
nirgends anders als in seinem Traité de
mécanique beschrieben worden ist, so wird es nicht
uͤberfluͤssig seyn, dasselbe hier gaͤnzlich auseinander
zu sezen.
Theilt man die Basis ag (Fig. 44) einer solchen
Figur in eine gerade Anzahl gleicher Theile, z.B. in sechs, zieht aus den
Theilungspunkten die Ordinaten bb', cc', dd' etc.,
und betrachtet die auf diese Weise erhaltenen Flaͤchen als Trapezoide, so
wird der Flaͤcheninhalt der Figur aa'c'c
oder
S = ½ ab (aa' + bb') +
½ bc (bb'
+ cc') seyn oder da ab = bc ist,
S = ½ ab (aa' + 2bb' + cc')
theilt man die Linie ac in
drei gleiche Theile und zieht aus den erhaltenen Theilungspunkten die Ordinaten nn' und mm', so
wird der naͤmliche Flaͤcheninhalt ebenfalls wie folgt
ausgedruͤkt werden koͤnnen.
S = ½ an (aa' + 2nn' + 2mm' + cc'.)
Da aber an = ⅓ ac ist, so ist auch ½ an =
⅓ ab; ferner ist, da nb = mb ist, bb' = ½ (nn' + mm') und 4bb' = 2 (nn' +
mm').
Fuͤhrt man diese Werthe in die Gleichung ein, so erhaͤlt man
S = ⅓ ab (aa' + 4 bb' +
cc'.)
Auf gleiche Weise findet man, daß der Flaͤcheninhalt der Figur cc'd'e'ec oder
S' = ⅓ ab (cc' + 4 dd' +
ee')
und der Flaͤcheninhalt der Figur ee'f'g'ge oder
S'' = ⅓ ab (ee' + 4 ff' +
gg') sey.
Es ist hiemit der Inhalt der ganzen Figur:
Z = ⅓ ab (aa' + gg' + 2
(cc' + ee')
+ 4 (bb' + dd' +
ff'))
um also den Flaͤcheninhalt einer solchen Figur zu
berechnen, hat man nur deren Basis in eine gerade Anzahl gleicher Theile zu theilen.
Derselbe wird alsdann gleich dem Drittel des Productes eines solchen Theiles und der
Summe der aͤußersten Ordinaten vermehrt mit der doppelten Summe der
uͤbrigen Ordinaten von ungeradem Range, und der vierfachen Summe der
Ordinaten von geradem Range seyn.Sind die beiden geraden Seiten aa' und gg' weder zu einander parallel noch
senkrecht auf die Abscissenlinie ag (Fig.
45), so verlaͤngere man dieselbe und ziehe von den beiden
aͤußersten Punkten der Curve die Ordinaten a'm und g'n, theile die erhaltene
Abscisse mn in eine gerade Anzahl gleicher
Theile ein und verfahre wie vorhin. Man erhaͤlt auf diese Weise den
Flaͤcheninhalt der Figur m'a'd'g'n.
Fallen nun die beiden Ordinaten a'm und g'n innerhalb des gegebenen Raumes, so sind die
Flaͤcheninhalte der durch die Seiten desselben und die
Huͤlfsordinaten gebildeten Dreieke aa'm
und gg'n zu dem erhaltenen
Flaͤcheninhalte zu addiren; fallen diese Ordinaten aber außerhalb des
gegebenen Raumes (wie es die Figur zeigt), so sind die
Flaͤcheninhalte der gebildeten Dreieke davon abzuzaͤhlen; und
man erhaͤlt alsdann den wirklichen Inhalt der gegebenen
Flaͤche.Ist die gegebene Flaͤche von lauter Curven (Fig. 46)
eingeschlossen, so theile man dieselbe durch irgend eine Linie in zwei
Theile und berechne dann jeden dieser Theile besonders. Laßt uns nun diese Berechnungsart auf die Bestimmung des Inhaltes der Figur
anwenden, welche den dynamischen Effect des durch Expansion wirkenden Dampfes
ausdruͤken kann.
Nehmen wir als Beispiel einen Dampf von zwei Atmosphaͤren an, dessen Druk
hiemit = 20660 Kilogr. auf den Quadratmeter (ungefaͤhr 30 Pfd. auf den
Quadratzoll) ist, und lassen wir diesen Dampf in den Cylinder von A bis auf die Hoͤhe von d (Fig.
47) einstroͤmen, so wird derselbe in dem Punkte e, wo er alsdann ein doppeltes Volumen hat, nur noch
eine halb so große Tension oder 10330 Kilogr. auf den Quadratmeter, in dem Punkte
f hingegen nur 6886 2/3 Kilogr. haben.
Druͤkt man daher die anfaͤngliche Tension oder dd' durch 20660 Kilogr. aus, so wird:
e
e'
= 10330 Kilogr.
ff'
= 6886 2/3 –
g
g'
=
5165 –
h
h'
=
4132 –
ii'
= 3443 1/3 –
B
B'
= 2951 3/7 – seyn.
Der Inhalt dieser Figur, welche den dynamischen Effect dieser Menge Dampfes durch
siebenfache Expansion ausdruͤkt, ist daher =
(Ad + Ac) + ⅓ Ad (dd' + BB' + 2 (ff' + hh') + 4 (ee' +
gg' + ii'))
= Ad × 20660 + ⅓
Ad (60220 + 2951 3/7 + 2 (6886 ⅔ +
4132) + 4 (10330 + 5165 + 3443 ⅓))
= Ad (20660 + ⅓ ×
121402 2/21)
= 61027 Kilogr. × Ad.
Dieser Ausdruk des Flaͤcheninhaltes der Figur ACd'B'BA ist begreiflicher Weise etwas zu groß, da wir angenommen haben,
daß sie aus lauter Trapezoiden bestehen, und daß daher d'e', e'f' gerade Linien seyen, welche
in der Wirklichkeit concave Linien sind.
Je groͤßer hingegen die gerade Anzahl gleicher Theile ist, in welche man die
Linie AB eintheilt, desto genauer wird der
Flaͤcheninhalt der gegebenen Figur ausgedruͤkt werden.
Laßt uns z.B. die Linie AB in eine doppelte Anzahl,
hiemit in 14 gleiche Theile theilen. Man erhaͤlt alsdann noch folgende
Ordinaten:
mm
= 2/3 ×
20660
= 13773 1/3
nn'
= 2/3
–
= 8264
oo'
= 2/7
–
= 5902 6/7
pp'
= 2/9
–
= 4591 1/9
qq'
= 2/11
–
= 3756 4/11
rr'
= 2/13
–
= 3178 6/13
und folgenden Flaͤcheninhalt der Figur:
S = Ad × 20660 +
⅙ Ad (20660 + 2951 2/7 + 2 (10330 + 6886
⅔ + 5165 + 4132 + 3443 ⅓) + 4 (13773 ⅓ + 8264 + 5902 6/7 + 4591
1/9 + 3756 4/11 + 3178 6/13))
= Ad × 20660 + ⅙
Ad (23611 3/7 + 59914 + 157864 ½)
= Ad (20660 + ⅙ ×
241389 13/14)
= Ad × 60891 Kilogr.
Wuͤrde man endlich die Linie AB in eine noch
groͤßere Anzahl gleicher Theile eintheilen, so wuͤrde man sich immer
mehr dem wirklichen Ausdruke naͤhern. Man findet alsdann ungefaͤhr
folgenden:
S = Ad × 60862
Kilogr.
Da nun 60862 Kilogr. den Gesammtdruk des Dampfes auf 1 Quadratmeter
Oberflaͤche bedeutet, so erhaͤlt man, wenn wir Ad = 1 Meter annehmen:
S = 60862 Kilogramm-Meter,
welches der dynamische Effect ist, den 1 Kubikmeter Dampf von
2 Atmosphaͤren durch siebenfache Expansion hervorbringt.
Auf gleiche Weise hat Poncelet folgende Werthe fuͤr
die dynamischen Effecte berechnet, welche 1 Kubikmeter Dampf von 1
Atmosphaͤre Tension durch eine mehr oder weniger große Expansion
hervorbringt.
Volumen nach
der Ausdehnung.
Dynamischer Effect
in Kubikmeter.
Volumen nach
derAusdehnung.
Dynamischer Effect
inKubikmeter.
1,00
10330
5,75
28339
1,25
12635
6,00
28839
1,50
14518
6,25
29261
1,75
16111
6,50
29665
2,00
17490
6,75
30055
2,25
18707
7,00
30431
2,50
19795
7,25
30794
2,75
20780
7,50
31144
3,00
21679
7,75
31483
3,25
22506
8,00
31811
3,50
23271
8,25
32129
3,75
23984
8,50
32437
4,00
24650
8,75
32736
4,25
25277
9,00
33027
4,50
25867
9,25
33310
4,75
26426
9,50
33585
5,00
26955
9,75
33854
5,25
27459
10,00
34116
5,50
27940
Da nun die dynamischen Effecte zweier Gasarten, welche man um die naͤmliche
Portion ihres anfaͤnglichen Volumens ausdehnen laͤßt, sich zu einander
verhalten, wie die Producte ihrer Tensionen in ihre Quantitaͤten, so hat man,
um den Effect irgend einer Quantitaͤt Dampfes von einer gegebenen Tension zu
wissen, nur den der naͤmlichen Ausdehnung entsprechenden Effect in der
vorstehenden Tabelle aufzusuchen, und denselben mit dem Producte der gegebenen
Quantitaͤt und Tension zu vervielfachen.
Beispiel: Wie viel betraͤgt der dynamische Effect
von 1 Kubikmeter Dampf von 4 Atmosphaͤren, welcher mit fuͤnffacher
Expansion wirkt?
Antwort: Derjenige von 1 Atm. betraͤgt 26955 Kil.
Meter, derjenige von 4 Atm. hiemit 4 × 26955 = 107820 Kil. Meter.
Theoretisches Verfahren, um diesen dynamischen Effect zu
berechnen.Gleichung der Expansionscurve.
Druͤkt a den Druk aus, welchen der vollwirkende
Dampf auf 1 Quadratmeter Section des Kolbens ausuͤben kann, b die Hoͤhe, bis zu welcher man den Dampf in den
Cylinder AB (Fig. 48)
einstroͤmen laͤßt, so stellt der Flaͤcheninhalt der Figur ABCDE, welche einerseits von einer geraden Linie,
andrerseits von der Expansionscurve eingeschlossen ist, den dynamischen Effect des
durch Expansion wirkenden Dampfes aus.
Diese Curve hat folgende correspondirende Abscissen und Ordinaten:
Abscissen.
Ordinaten.
x
= b
y
= a
x'
= 2b
y'
= a/2
x''
= 3b
y''
= a/3
x'''
= 4b
y'''
= a/4 etc.
Die Gleichung dieser Curve ist daher folgende vom ersten Grade:
y = ab/x.
Dann sezt man z.B. x = 4b, so
wird y =
ab/4b = a/4.
Ist x = o, so wird y unendlich,
und
ist y = o, so wird x unendlich;
daher diese Curve keine geschlossene ist, und niemals die
Abscissenlinie erreicht, obschon sie sich derselben immer mehr und mehr
naͤhert.
Flaͤcheninhalt dieser Curve.
Es sey AD (Fig. 49) unendlich nahe
bei BC, so ist DC das Differential von FD und daher
DC = d (FD) = d (x).
Es kann ferner AD = BC und die Figur ABCD hiemit als ein
Parallelogramm angenommen werden, dessen eine Seite AD = y und dessen andere Seite = DC = d (x) ist.
Der Flaͤcheninhalt derselben ist daher = y. d (x).
Derselbe ist aber auch, da er unendlich klein ist, im Verhaͤltnisse zu
demjenigen der Figur AMFD, das Differential
desselben, daher
y.
d (x)
= d (AMFD)
= d (v)
und hiemit v
= S (y . d(x)).
Dieß ist die allgemeine Gleichung, vermittelst welcher man den Flaͤcheninhalt
einer jeden Curve berechnen kann. Vereinigt man nun diese Gleichung mit derjenigen,
welche der Expansionscurve angehoͤrt, oder mit
y = ab/x,
so erhaͤlt man:
Textabbildung Bd. 47, S. 407
Ersezt man diesen Nepperschen Logarithmus durch denjenigen, dessen Basis = 10 ist, so
erhaͤlt man:
v = ab. 2,30 . lg (x).
Dieser Werth druͤkt allein den dynamischen Effect aus, welchen der Dampf durch
seine Expansion producirt.
Es muß zu demselben noch derjenige gezaͤhlt werden, welchen der Dampf ohne
Expansion auf den Kolben ausuͤbt, und welcher durch den Flaͤcheninhalt
des Parallelogrammes EFMG ausgeuͤbt werden
kann.
Derselbe ist aber = EF × EF = ab.
Es ist daher der totale dynamische Effect oder:
V = ab + ab. 2,3 . lg (x)
= ab (1
+ 2,3 . lg (x)),
Sezt man b = 1 Meter, so erhaͤlt man:
V' = a (1 + 2,3 . lg (x)),
welches, da a den Druk des Dampfes
auf 1 Quadratmeter Section bezeichnet, den dynamischen Effect von 1 Kubikmeter
Dampfes angibt, und wo x das Verhaͤltniß des
anfaͤnglichen Volumens zum expandirten Volumen des Dampfes bedeutet.
Wuͤrde man diesen Werth mit dem Gewichte P von 1
Kubikmeter solchen Dampfes, dessen Pression = a ist,
vervielfachen, so erhaͤlt man den dynamischen Effect von 1 Kil. Dampf,
oder:
V'' = Pa (1 + 2,3 .
lg (x)).Dieß ist auch die Formel, auf welche Fourier und
Dufour durch ihre Berechnungen gekommen
sind.
Vermittelst dieser Formeln ist folgende Tabelle fuͤr Dampf von 1 Atm. Druk
berechnet worden, deren Werthe von denjenigen, welche Poncelet durch das praktische Verfahren gefunden hat, nur sehr wenig
verschieden sind.
Textabbildung Bd. 47, S. 408
Werthe von x oder Volumen des
Dampfes nach des Ausdehnung; Werth von 1 + 2,50 . lg (x); Werth von V'; Werth
von V''
Beispiel. Es sey der Diameter des Kolbens = 0m,4 so ist seine Section = 0,7854 × (0m,4)² = 0,12566 Quadratmeter.
Stroͤmt nun der Dampf in den Cylinder bis auf die Hoͤhe von 0m,32, so wird das Volumen des bei jedem Kolbenzuge
hineingestroͤmten Dampfes = 0m,32 ×
0,12566 = 0,0402125 Kubikmeter seyn, und betraͤgt die Hubslaͤnge 1m,44, so wird der Dampf eine 1m,44/0m,32 = 4
1/2fache Expansion erleiden. Fuͤr diese Ausdehnung gibt die Colonne III der
obigen Tabelle fuͤr den Effect von 1 Kubikmeter Dampf von 1
Atmosphaͤre anfaͤnglicher Tension, 25850 Kil. Mtr. und fuͤr
denjenigen hiemit von 0,0402125 Kubikmeter, 25850 × 0,0402125 = 1039,5 Kil.
Mtr. an.
Betraͤgt nun die Tension des Dampfes 3 1/2 Atmosphaͤren, so wird
derselbe = 3 1/2 × 1039,5 = 3638 Kil. Mtr. seyn. Geschehen endlich 15 doppele
Kolbenzuͤge per Min., so ist der theoretische
Effect dieser Maschine per Secunde = (3638 × 2
× 15)/60 = 1819 Kil. Mtr. = 24 Pferdekraͤfte.
Nehmen wir nun an, der Dampf stroͤme fortwaͤhrend in den Dampfcylinder,
und es habe also keine Expansion Statt, so wuͤrde zwar bei jedem einfachen
Kolbenzuge ein Effekt von 36150k × 0m,12566 × 1m,44 = 6541 Kil. Mtr. hervorgebracht werden, welcher fast doppelt so groß als
ersterer waͤre; dazu wuͤrde eben auch ein 4 1/2 Mal so großes Volumen
Dampfes und hiemit auch eine 4 1/2fache Menge Brennmateriales erfordert werden.
Da aber die Wirksamkeit einer Maschine nicht nach dem absoluten Effecte, welchen
dieselbe hervorbringen kann, sondern nach demjenigen geschaͤzt wird, welchen
eine gewisse Quantitaͤt Dampfes oder Brennmateriales erzeugt, so folgt
hieraus, wie groß der Nuzen ist, den man aus der Expansion des Dampfes ziehen
kann.
Je groͤßer diese leztere ist, desto groͤßer wird auch der
hervorgebrachte Effect einer gegebenen Quantitaͤt Dampfes seyn. Indessen
sieht man doch aus vorstehenden Tabellen, daß man eigentlich nur
betraͤchtlichen Vortheil hat, wenn man den Dampf mit geringer Expansion
arbeiten laͤßt. Der Dampf wird z.B. bei 2 3/4facher Expansion
ungefaͤhr den doppelten dynamischen Effect hervorbringen, als wenn er ohne
Expansion wirkte. Um hingegen einen dreifachen Effect hervorzubringen, bedarf es
schon einer siebenfachen, und fuͤr einen vierfachen wuͤrde
ungefaͤhr eine zwanzigfache Ausdehnung erfordert werden. Eine solche
Expansion kann aber, wie aus den folgenden Betrachtungen zu ersehen ist, nur dann
ohne Nachtheil Statt finden, wenn man Dampf von sehr hoher Tension verwendet.
Die Expansion des Dampfes kann naͤmlich natuͤrlicher Weise nur so weit
mit Vortheil getrieben werden, bis der Gegendruk, den der Kolben erleidet, dem Druke
des Dampfes am Ende seiner Ausdehnung gleichkommt. Uebertrifft jener denselben
sogar, so kann die weitere Fortbewegung des Kolbens nur auf Kosten der schon
erhaltenen Wirkung noch Statt haben.
Die Versuche mangeln, um diesen Gegendruk gehoͤrig angeben zu koͤnnen
(Tretgold's Angaben sind fast die einzigen, und auch
diese scheinen ziemlich unzuverlaͤssig zu seyn); das Verhaͤltniß
desselben zum anfaͤnglichen Dampfdruke wuͤrde die Zahl angeben, um wie
viel Mal der Dampf hoͤchstens ausgedehnt werden koͤnne, damit kein
Nachtheil entstehe.
Immerhin ist es offenbar, daß der Dampf in Maschinen mit Condensation eine mehrfache
Expansion erleiden darf als in solchen ohne Condensation; denn anstatt des
Gegendrukes (1k,033 auf den Quadratcentimeter),
welcher bei lezteren durch den Druk der atmosphaͤrischen Luft entsteht, kommt
bei ersteren nur derjenige weit kleinere (0k,15
auf den Quadratcentimeter) in Rechnung, welchen die Unvollkommenheit der
Condensation veranlaßt. Die andere Portion des Gegendrukes, welcher von der
Kolbenreibung, von der Abkuͤhlung des Dampfes im Cylinder und in den
Dampfroͤhren, den verschiedenen Dampfverlusten und von anderen Ursachen herruͤhrt,
ist hingegen in beiden Faͤllen gleich groß.
Poncelet gibt den Nuzeffect bei Expansionsmaschinen mit
einem einzigen Cylinder zu 55/100 des auf obige Weise berechneten dynamischen
Effectes an.
Da die Abkuͤhlung des Dampfes, so wie die Kolbenreibung bei Maschinen mit zwei
Dampfcylindern groͤßer ist, als bei ersteren, so betraͤgt der
Nuzeffect nur 50/100 des dynamischen Effectes fuͤr die staͤrksten
Maschinen, 45/100 fuͤr diejenigen von der Kraft von 10–12 Pferden, und
40/100 fuͤr noch schwaͤchere. Ungeachtet dieses Vortheiles, welchen
die ersteren in Bezug auf den Nuzeffect haben, werden doch sehr oft die Maschinen
mit zwei Cylindern denselben wegen ihrer regelmaͤßigern Bewegung vorgezogen.
Außerdem koͤnnten die Maschinen mit einem einzigen Cylinder fast gar nicht
angewendet werden, in dem Falle, wo man dem Dampf eine vielfache Expansion erleiden
lassen will, da alsdann der Zufluß des Dampfes in das Steuerungsgehaͤuse
aͤußerst schnell eroͤffnet und wieder abgesperrt werden
muͤßte.
Tafeln