| Titel: | Astronomische Pendelwage, nebst einer neuen Nivellirwage, erfunden und dargestellt von Lorenz Hengler, akademischen Bürger an der Hochschule zu München. |
| Autor: | Lorenz Hengler |
| Fundstelle: | Band 43, Jahrgang 1832, Nr. XVI., S. 82 |
| Download: | XML |
XVI.
Astronomische Pendelwage, nebst einer neuen
Nivellirwage, erfunden und dargestellt von Lorenz Hengler, akademischen Buͤrger an
der Hochschule zu Muͤnchen.
Mit Abbildungen auf Tab.
II.
Hengler's astronomische Pendelwage.
Es ist allgemein bekannt, welche wichtige Rolle das Pendel sowohl im
wissenschaftlichen als civilen Leben spielt; seine ausgebreitete, mannichfaltige
Anwendung zu so vielen und verschiedenen Zweken macht es zu einem der wichtigsten
Instrumente. Doch scheint mir noch eine Seite uͤbrig zu seyn, von welcher es
noch nicht benuzt worden ist, wenigstens noch nicht so, wie es seiner Natur nach
haͤtte benuzt werden koͤnnen; – ich meine naͤmlich als
Instrument diejenigen bewegenden Kraͤfte zu messen, welche nicht in
paralleler Richtung mit der Schwere wirken.
Es ist naͤmlich bekannt, daß das Pendel, wenn es von der Schwere allein
afficirt wird, nur in vertikaler Lage ruht, und daß eine gewisse Kraft, die aber
nicht parallel mit der Schwere wirken darf, erfordert wird, dasselbe aus der
senkrechten Lage zu bringen, welche Kraft dem Sinus des
Elevationswinkels proportional ist; daher ließe sich durch das Pendel jede solche
einwirkende Kraft genau bestimmen. Allein da es viele Kraͤfte gibt, die im
Verhaͤltniß zur Schwere so gering sind, daß wir den Sinus des durch sie
erzeugten Elevationswinkels bei einem Pendel von der Laͤnge, die wir ihm zu
geben im Stande sind, unmoͤglich wahrnehmen koͤnnen; so sind wir auch
nicht im Stande, solche Kraͤfte durch ein gewoͤhnliches Pendel zu
messen. So wissen wir wohl, daß z.B. jeder Koͤrper auf der Oberflaͤche
der Erde gegen den Mond, gegen die Sonne etc. zu einer Zeit staͤrker
gravitiren muͤsse, als zu einer anderen, je nachdem er auf der, diesem
Koͤrper zu- oder abgewandten Seite sich befindet; und das Pendel
muͤßte diese Differenz seiner Natur nach genau anzeigen; allein hiezu
waͤre schon ein Pendel von mehreren tausend Fuß Laͤnge noͤthig,
um nur eine Spur von dieser Differenz wahrnehmen zu koͤnnen. Eben so
verhaͤlt es sich mit vielen anderen Kraͤften, welche alle ganz genau
durch das Pendel bestimmt werden koͤnnten, wenn wir im Stande waͤren,
ihm jede beliebige Laͤnge zu geben. –
Diese Schwierigkeit nun glaube ich durch eine Vorrichtung, die ich nachher
beschreiben werde, uͤberwunden zu haben, so daß man im Stande ist ein Pendel, oder
eigentlich eine PendelwageDenn es ist ein Mittelding zwischen Pendel und Wage, wie aus der Theorie
erhellen wird. Ich gab ihm den Namen „astronomische Pendelwage,“ weil sie
vorzuͤglich fuͤr astronomische Untersuchungen bestimmt
ist. zu verfertigen, die an Empfindlichkeit einem gewoͤhnlichen Pendel von
jeder, selbst von unendlicher Laͤnge gleichkommt, und man daher ein
Instrument hat, jede auch noch so geringe Kraft, welche nicht in paralleler Richtung
mit der Schwere wirkt, zu messen. –
§. 1.
Princip dieser Pendelwage.
Diese Pendelwage beruht auf dem Princip, daß man ein Pendel in einer gegen den
Horizont geneigten Ebene schwingen laͤßt, anstatt in einer senkrechten, wie
es bei gewoͤhnlichen Pendeln der Fall ist, und hier gilt folgender
Lehrsaz:
„Bei einem in schiefer Ebene schwingenden Pendel verhaͤlt sich die
Elevationskraft zur Schwere, wie das Produkt aus dem Sinus des in dieser Ebene
beschriebenen Elevationswinkels in den Sinus des Neigungswinkels der schiefen
Ebene zu dem Produkte aus der Laͤnge des Pendels in die Laͤnge der
schiefen Ebene; oder wenn
γ, die genannte Kraft,
G, die Schwere,
a, der Sinus des Elevationswinkels,
L, die Laͤnge der schiefen Ebene,
l, die Laͤnge des Pendels und
α, der Sinus des Neigungswinkels
ist; so verhaͤlt sich γ : G = aα : lL; also
γ = aα/lL . G.“
Beweis.
1) Es sey ABCD
Fig. 20 eine
Ebene, die gegen den Horizont unter dem Winkel EAD
geneigt ist, und daher ED der Sinus des
Neigungswinkels.
In F sey ein Koͤrper, so bewegt sich dieser in der
Richtung FH (wenn FH
perpendikular auf AB ist) mit einer Kraft, die sich zur
Schwere verhaͤlt, wie DE : AD, oder wenn diese Kraft = g, die Schwere =
G ist; so verhaͤlt sich g : G = ED : AD, daher
g = ED/AD . G;
oder wenn diese Bewegung entweder durch eine Unterlage mn oder durch den Faden KF
gehindert wird, so wird der Faden mit der naͤmlichen Kraft g gespannt, oder die Unterlage gedruͤkt. (In
diesem Falle ist mn # AB und
KF senkrecht auf AB.)
2) Denkt man sich die Unterlage aber so, daß sie die Lage uv, oder den Faden, daß er die Richtung MF
(senkrecht auf uv) hat, so wird auch jezt wieder die
Kraft g in zwei Kraͤfte zerlegt, wovon die eine
auf die Unterlage uv druͤkt, die andere den
Koͤrper in der Richtung Fu bewegt, und wenn diese
leztere = γ ist, so verhaͤlt sich (weil
∆ Fp ∆ uFm mFM) γ : g = mF : MF und nach N. 1
g : G
= ED
:
AD
––––––––––––––––
γ : G
= mF
×
ED : MF × AD das heißt:
da mF der Sinus des Elevationswinkels = a
ED der Sinus des Neigungswinkels = α
MF die Laͤnge des Pendels = I
AD die Laͤnge der schiefen Ebene = L,
γ : G = aα : lL also γ = aα/lL G.
Da sowohl der Winkel EAD als auch der Winkel mFu = mMF beliebig genommen
ist, so gilt der Beweis natuͤrlich fuͤr jeden anderen, also allgemein.
–
§. 2.
Beschreibung des Instrumentes.
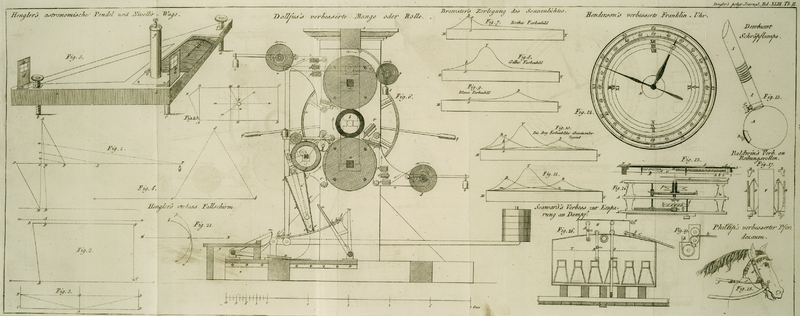
Siehe Fig. 1.
Um einen Koͤrper in einer gegen den Horizont geneigten Ebene schwingen zu
lassen, wobei die Reibung fast gaͤnzlich aufgehoben ist, mache man folgende
Einrichtung:
Es seyen A und B senkrecht
uͤbereinanderstehende feste Punkte; DH und AF zwei Faͤden, welche in A und H befestigt sind, und den Hebelarm DP, dessen Schwerpunkt nach P faͤllt, in horizontaler Lage halten; so wird dieser Hebelarm nur
in einer mit der Linie MN (welche durch H und B gezogen ist)
parallelen Lage ruhen, und jedes Mal wieder dahin zuruͤkkehren, wenn er durch
irgend eine Kraft aus dieser Lage gebracht worden ist, oder eigentlich nach Art
eines Pendels hin- und herschwingen, und zwar in einer schiefen Ebene, deren
Neigungswinkel = < HAB ist. Man mag daher ein
Gewicht oder eigentlich den Schwerpunkt des Hebelarmes auf jeden beliebigen Punkt
desselben uͤbertragen, so beschreibt er Schwingungen in einer unter dem
Neigungswinkel HAB gelegten Ebene, wobei die
Laͤnge des Pendels dem Abstand von dem Punkte Z
(wenn dieses der Punkt ist, wo die Linie HA den Hebelarm
schneidet) proportional ist.
Denn man waͤhle sich den Punkt F, ziehe Fu senkrecht auf AH und
drehe den Hebelarm um die Linie AH als Axe (denn diese
ganze Linie ist unbeweglich, weil die Punkte A und H unbeweglich sind), so beschreibt die Linie F eine Kreisflaͤche und F einen Kreis
in einer Ebene, welche gegen den Horizont unter dem Winkel uFz = HAB geneigt ist, was sogleich
einleuchtet, wenn man sich das ∆ AFu als festen
Koͤrper denkt, welcher alsdann einen Kegel beschreibt, dessen Axe Au ist und dessen Grundflaͤche uF zum Radius hat. Aus dem naͤmlichen Grunde
beschreiben die Punkte x, P, Kreise in einer schiefen
Ebene, deren Neigungswinkel vxz = wPz = uFz = HAB
sind und deren Radien dem Abstande von z proportional
sind, d.h. fuͤr den Punkt P ist Pw, fuͤr x ist xv der Radius.
Will man nun die Kraft γ, die erfordert wird, fuͤr den
Elevationswinkel, dessen Sinus = a ist, obige Gleichung
hier anwenden, so ist HB der Sinus des Neigungswinkels
der schiefen Ebene = a,
AH die Laͤnge derselben = L
wP die Laͤnge des Pendels = l; daher
γ = (a.HB)/(AH.wP) G,
oder da man, wenn der Winkel HAB =
wPz sehr klein ist (wie hier gewoͤhnlich),
ohne merklichen Fehler AB statt AH, und Pz statt Pw sezen kann; so ist auch
γ = (a.HB)/(AB.Pz) G.
§. 3.
Hauptpunkte zur Beruͤksichtigung bei Verfertigung
dieser Wage.
1) Die Punkte A und D
muͤssen unbeweglich fest seyn; es wird daher zur Aufstellung dieses
Instrumentes ein eben so festes Lokal erfordert, als zu irgend einem anderen
astronomischen Instrumente.
2) Die Faͤden AF und DH duͤrfen keine drehende Kraft haben, auch keine bekommen durch
jede barometrische, hygrometrische und thermometrische Veraͤnderung; sie
duͤrfen daher nicht aus geflochtenen oder gesponnenen Stoffen seyn, sondern
aus gewobenen oder reinen Naturprodukten, z.B. ungesponnener Seide, Roßhaar etc.
3) Alle fremden Kraͤfte muͤssen abgehalten werden, besonders Luftzug,
oder auch Magnetismus, Elektricitaͤt etc. Der Hebelarm darf daher nicht aus
Eisen oder uͤberhaupt aus keinem Material, auf welches Magnetismus oder
Elektricitaͤt besonderen Einfluß haben, verfertigt werden. Um den Luftzug
moͤglichst abzuhalten, wird das ganze Instrument hermetisch verschlossen, so
daß nur bei P mittelst eines Mikroskopes der Hebelarm
betrachtet werden kann, der sich dort in eine feine Spize endigt, unter welcher eine
Skale angebracht ist.
4) Auch ist noch eine Vorrichtung zu treffen, den Hebelarm in Ruhe zu bringen; denn
sonst waͤre man genoͤthigt den Stand desselben durch die
Graͤnzen der Oscillation selbst zu bestimmen, weil der Hebelarm, wenigstens
nach meinen bisherigen Beobachtungen niemals ganz ruhig ist.
§. 4.
Leichtere Bestimmung der Kraft (γ).
Aus der Gleichung γ = (a.H)/(AB.Pz) G (§. 2.)
laͤßt sich die Kraft γ zwar theoretisch
ganz genau bestimmen; allein wenn das Instrument bei maͤßiger Groͤße
sehr empfindlich seyn soll, so muß HB so klein werden,
daß man es unmoͤglich genau messen kann; und es ist daher in diesem Falle
wuͤnschenswerth, ein anderes Mittel zu haben, wodurch diese Kraft γ bestimmt werden kann. Ein solches Mittel ist
die Schwingungszeit des Hebelarmes. Es ist naͤmlich aus der Pendellehre
bekannt, daß sich bei gleichen Pendellaͤngen die Schwingungszeiten verkehrt
verhalten, wie die Quadratwurzeln der bewegenden Kraͤfte; oder wenn ein
Pendel, bei welchem eine Kraft = G wirkt, eine
Schwingungszeit = t hat, ein anderes aber von gleicher
Laͤnge, bei welchem eine Kraft = g wirkt, eine
Schwingungszeit = nt hat; so verhaͤlt sich G : g = n²t² : t². – Wenn nun t eine Sekunde, also nt, n Sekunden bedeutet,
so verhaͤlt sich G : g = n² : t.
Nun aber verhaͤlt sich bei einem Sekundenpendel, dessen Laͤnge = λ, die Elevationskraft = λ fuͤr den Elevationswinkel, dessen Sinus a ist, zu der bewegenden Kraft g oder γ : g = a : λ
und nach oben
g : G
= r : n², also
–––––––––––––
γ : g
= a : λn² daher
γ = a/λn² G.
Auf diese Art laͤßt sich nun γ sehr leicht
bestimmen. Es sey z.B. die Schwingungszeit oder
n = 100 Sekunden und
a = 1 Linie
λ = 306 Linien; so ist
γ = 1/3060000 G.
§. 5.
Resultate aus meinen bisherigen Versuchen.
Aus der Theorie dieser Pendelwage ergibt sich von selbst, daß sie ein Instrument ist,
durch welches jede, selbst die geringste bewegende Kraft gemessen werden kann; denn
um nur Ein Beispiel der Empfindlichkeit anzufuͤhren,
so sey
n = 1000 (in obiger
Bedeutung)
a = 0,001 Linie (denn durch
ein Mikroskop von
100maliger Linearvergroͤßerung
koͤnnen wir 0,001 Linie noch
genau unterscheiden), so
ist
γ = 0,001/306.1000000 G =
1/306000000000 G.
Dieses habe ich auch durch meine Versuche bestaͤtigt gefunden.
1) Meine ersten Versuche richteten sich auf die Attraction der Sonne und des Mondes.
Zu diesem Zweke ließ ich in einem Zimmer von 16' Hoͤhe meine Wage, dessen
Hebelarm 10' Laͤnge hatte, anbringen, suchte hiezu zwei Punkte aus, den einen
oben an der Deke des Zimmers, den anderen unten auf dem Boden desselben, die mir die
festesten schienen und zugleich eine solche Lage hatten, daß der Hebelarm eine
Schwingungszeit von 5 Minuten erhielt. Die Empfindlichkeit der Wage war daher sehr
groß; denn γ = a/(306.90000) G, und da ich mittelst des oben
genannten Mikroskopes 0,001 Linie noch genau unterscheiden konnte, so war ich im
Stande eine Kraft zu messen, welche = 1/(90000.306.1000) G = 1/27540000000 G war.
Dieses Instrument verschloß ich hermetisch, so daß nur der Hebelarm bei P mittelst des Mikroskopes betrachtet werden konnte. Ich
stellte nun im Neumonde des Monats Maͤrz die Wage so, daß der Hebelarm
Mittags 12 Uhr in der Mittagslinie ruhte, und nun machte er folgende Oscillationen:
Von 12 Uhr an zog er sich immer mehr und mehr gegen Westen, bis etwas nach 3 Uhr;
kehrte dann wieder allmaͤhlich zuruͤk, so daß er etwas nach 6 Uhr
wieder in der Mittagslinie stand; zog sich dann nach und nach hinuͤber gegen
Osten, bis nach 9 Uhr; kehrte dann allmaͤhlich wieder zuruͤk, so daß
er gegen 12 1/2 Uhr wieder in der Mittagslinie stand. Diese Oscillationen
wiederholte er immer in der naͤmlichen Zeit, wovon ich mich zwei Monate lang
taͤglich uͤberzeugte. Wenn ich die Graͤnzen der Oscillationen
an verschiedenen Tagen verglich, so zeigte es sich, daß sie am groͤßten waren
zur Zeit des Neu- und Vollmondes; am kleinsten aber in den Quadraturen. Das
taͤgliche Ab- und Zunehmen aber auch nur einiger Maßen zu bestimmen,
bin ich wegen der Untauglichkeit des Lokales nicht im Stande und kann also nur das
als unbezweifeltes Endresultat annehmen, daß diese Oscillationen der Wage wirklich
von der Attraction der
Sonne und des Mondes herruͤhrten; bin aber auch uͤberzeugt, daß man
die Attractionskraft des Mondes selbst und daher auch seine Maße durch dieses
Instrument genau bestimmen kann, sobald man ein dazu taugliches Lokal hat.
2) Versuche anderer Art stellte ich an in Beziehung auf die Kraft, mit welcher ein
Koͤrper sich gegen den Aequator zu bewegen strebt, wegen der Axendrehung der
Erde. Zu diesem Zweke machte ich folgende Vorrichtung:
(Siehe Fig. 2.)
In einem Gebaͤude von 100 Fuß Hoͤhe suchte ich zwei moͤglichst
feste Punkte A und B (wenn
mn das Dach und uv den
Boden des Gebaͤudes vorstellen), brachte meine Wage so an, daß der Faden AF 1/2 Fuß, also BD 99 1/2
Fuß lang und der Hebelarm folglich ganz oben war; anstatt das Gewicht unmittelbar in
P anzubringen, befestigte ich dasselbe mittelst
eines Fadens PQ so, daß es beinahe auf dem Boden war;
regulirte nun die Wage so, daß der Hebelarm senkrecht auf der Ebene des
Mittagskreises stand, zog endlich das Gewicht von Q nach
P hinauf, und so zog sich auch der Hebelarm nach
Suͤden und zwar so bedeutend, daß ich schon bei einer Erhoͤhung von
einigen Fuß eine Differenz wahrnehmen konnte. Die Wage war natuͤrlich
hermetisch verschlossen, hatte die naͤmliche Empfindlichkeit wie oben und das
naͤmliche Mikroskop zur Beobachtung. Obgleich diese Versuche in kurzer Zeit
sehr oft wiederholt und abgeaͤndert werden koͤnnen, und man also in
kurzer Zeit genaue Resultate erhalten kann, zumal da alle jene
Unregelmaͤßigkeiten, welche aus Temperaturwechsel etc. entstehen, hier wegen
Kuͤrze der Zeit, welche zu einem Versuche noͤthig ist,
gaͤnzlich wegfallen; so habe ich doch bis jezt noch nicht genau bestimmen
koͤnnen, wie viel fuͤr jeden Fuß Erhoͤhung des Gewichtes der
Hebelarm gegen Suͤden sich wendet, und kann einstweilen nur das als bestimmt
behaupten, daß diese Wage wirklich eine solche Empfindlichkeit hat, daß sie durch
genannte Kraft afficirt, diesen Ausschlag gibt und zugleich ein directer Beweis
fuͤr die Axendrehung der Erde ist.
3) Ich stellte noch Versuche anderer Art an, wovon ich aber keine bestimmten
Resultate wegen Untauglichkeit meines Lokales geben kann. Diese Versuche betreffen
naͤmlich die Frage: „ob alle Materie gleich gravitire gegen den
Mond und gegen die Sonne.“
Es ist naͤmlich klar, daß wenn man zwei oder mehrere in jeder Beziehung ganz
gleiche Wagen dieser Art haͤtte und auf jede derselben ein Gewicht der
naͤmlichen Materie legen wuͤrde, alle zu gleicher Zeit den
naͤmlichen Ausschlag gegen den Mond und gegen die Sonne geben muͤßten.
Waͤren aber die Gewichte von verschiedener Materie, so konnten sie nur dann
gleichen Ausschlag geben, wenn alle Materie gleich gravitirte; allein
hieruͤber etwas Bestimmtes sagen zu koͤnnen, reichen meine bisherigen
Versuche nicht hin.
§. 6.
Anwendung dieser Wage als Nivellirwage.
Vielleicht konnte diese Wage noch in manchen anderen Faͤllen ihre Anwendung
finden, wenigstens glaube ich auf diese Art eine Nivellirwage verfertigen zu
koͤnnen, die manche Vorzuͤge vor den anderen haben moͤchte. Daß
man durch bisherige Instrumente nicht im Stande ist vollkommen zu nivelliren, ja daß
man hoͤchstens nur bis zu einer Sekunde mit Sicherheit nivelliren kann,
bedarf keines Beweises; denn abgesehen von zufaͤlligen
Unregelmaͤßigkeiten, liegt schon in der Theorie die Unmoͤglichkeit
vollkommenen nivelliren (ich meine naͤmlich die sogenannten Blasenivellen,
welche doch fuͤr die besten gehalten werden); denn auch zugegeben, daß man
die obere Flache des Nivells vollkommen eben geschliffen habe, so ist man nie im
Stande die Blase in die Mitte zu bringen, weil sie, einmal in Bewegung gesezt, sich
mit beschleunigter Schnelligkeit bis zum anderen Ende des Nivells fortbewegen muß,
und man hat also eine auf die Spize gestellte Nadel. Ganz anders aber
verhaͤlt es sich mit einem Nivell nach Art der astronomischen Pendelwage;
denn hier liegt es in der Willkuͤhr, dem Nivell jede denkbare Empfindlichkeit
zu geben, so daß man im Stande ist, nicht nur einzelne Sekunden, sondern selbst
hundertste Theile einer Sekunde mit groͤßter Sicherheit zu messen. Um nur ein
Beispiel von der großen Empfindlichkeit zu geben, so nehme man ein Nivell von etwas
großem Maßstabe. Es sey z.B. der Hebelarm zwei Fuß lang; man gebe ihm eine
Schwingungskraft = 100 Sekunden, so beschreibt der Hebelarm einen Winkel, dessen
Sinus = A ist. Nun aber laͤßt sich bei einem
Bogen, dessen Radius = zwei Fuß ist, noch ein Winkel von zwei Sekunden mittelst
eines maͤßigen Mikroskopes ganz deutlich wahrnehmen; daher ein Winkel des
Diopters = 2/16300 = 1/8150 Sekunden genau angeben. Obgleich nun ein solcher Winkel
auch fuͤr das staͤrkste Fernrohr gaͤnzlich verschwindet aber
vielleicht in kurzer Zeit durch Vervollkommnung der Heliotropen bestimmt werden
wird, so soll durch dieses Beispiel einstweilen nur gezeigt seyn, daß man dem Nivell
jede, fuͤr jeden Versuch noͤthige Empfindlichkeit geben kann. –
Um mich einer weitlaͤuftigen Beschreibung uͤberheben zu
koͤnnen, habe ich eine solche Nivellirwage durch Hrn. Mechanikus Weissenbach dahier verfertigen lassen, und dieselbe der
koͤnigl. Akademie der Wissenschaften vorgelegt. Sie ist auf Tab. II. in Fig. 5
abgebildet.
Die Theorie ist die naͤmliche wie bei der astronomischen Wage.
f ist der Hebelarm.
g und h sind die Anfhaͤngepunkte; durch die Schraube
a kann dem Hebelarm jede beliebige Empfindlichkeit gegeben werden; durch die
Schraube
b kann er in jede beliebige Lage gestellt werden.
d und e sind Dioptern, wovon eines beweglich seyn muß, um die Wage reguliren zu
koͤnnen.
Die drei Punkte a, c und b
bilden ein Dreiek, in welchem bei c ein rechter Winkel
ist.
Um das Diopter zu reguliren, waͤhle man sich einen Standpunkt A (siehe Fig. 3), messe in
entgegengesezter Richtung zwei gleiche Abstaͤnde AC und AB; errichte in jedem einen Stab
und visire aus A mit dem unregulirten Nivell nach dem
Stab B und C, so daß der
Hebelarm den naͤmlichen Standpunkt beibehaͤlt. Man bemerke die Punkte,
wo die Visirlinien die Staͤbe schneiden, genau; diese seyen D und F; mm visirt man von
F nach D und bemerkt den
Punkt, wo die Visirlinie den Stab A schneidet; es sey
dieß der Punkt G; endlich sezt man das Nivell in G, richtet das Diopter nach D oder F, waͤhrend der Hebelarm auf O gestellt wird. Dieses Nivelliren kann der Sicherheit
wegen oͤfters wiederholt werden. –
§. 7.
Hauptsaͤchliche Anwendungen dieser beiden
Instrumente.
I. Das
Nivellirinstrument.
Was dieses Instrument betrifft, so ist es uͤberhaupt uͤberall da
anzuwenden, wo sonst die gewoͤhnlichen Nivellen angewendet werden und
erreicht den Zwek des Nivellirens viel genauer, als alle anderen Nivelle, und
selbst in solchen Gegenden, wo andere Nivelle z.B. wegen zu niedriger Temperatur
ganz unbrauchbar werden. Dahin gehoͤren:
1) geometrische Messungen aller Art;
2) besonders aber feinere, astronomische Messungen, wo die gewoͤhnlichen
Nivelle viel zu unvollkommen sind;
3) die genaue Bestimmung der irdischen Strahlenbrechung in der
Atmosphaͤre, wobei ich folgende Bemerkungen zu machen fuͤr
noͤthig erachte.
Diese genannte Strahlenbrechung ist zu verschiedenen Zeiten und an verschiedenen
Orten so sehr variirend, daß ihre Differenz bei geometrischen Messungen mehrere
Minuten ausmacht, und ist bis auf diesen Tag noch keinem bestimmten Geseze
unterworfen. Diese glaube ich nun auf folgende Art genau bestimmen zu
koͤnnen.
In einer Gegend, wo man eine bedeutende Flaͤche uͤbersehen kann,
messe man sich
eine Linie ab (s. Fig. 4), suche den
Mittelpunkt derselben c und endlich einen Punkt d, der so liegt, daß cdb ein gleichseitiges Dreiek ist. Man nivellire aus c nach a, b und d
Es ist klar, daß es hier gleichguͤltig ist, ob das Nivell regulirt
sey oder nicht, wenn man nur den naͤmlichen Standpunkt des
Hebelarmes beobachtet., so werden diese drei Punkte genau in einer Ebene liegen, auf welcher
der Radius der Erde, der durch c geht, senkrecht
steht, es mag die Refraktion was immer fuͤr eine seyn; denn da die
Abstaͤnde ac, bc und d c' gleich
sind, so muß auch die Refraktion bei allen gleiche Wirkung hervorbringen. Nun
bringe man das Nivell nach d, visire nach b und c, so sind auch
b und c, also auch
a, c, b ganz genau in einer horizontalen
Lage.Um versichert zu seyn, daß die Refraktion waͤhrend der Zeit des
Operirens selbst sich nicht geaͤndert habe, waͤre es
besser, wenn man zwei oder mehrere Nivelle haͤtte, um zu gleicher
Zeit sowohl in c als in d zu nivelliren.
Stellt man nun in den Punkt a ein Fernrohr, so wird
b bald zu hoch, bald zu tief liegen und daher
die Wirkung der Refraktion genau bestimmt werden koͤnnen. Allein da die
Refraktion in jeder anderen Hoͤhe und fuͤr jede andere Richtung
eine andere ist, so muß sie auch fuͤr diese Faͤlle bestimmt
werden. Zu diesem Zweke mache man in a in beliebigen
Hoͤhen Signalpunkte, eben so in c in einer
Hoͤhe, welche nur die Haͤlfte der Hoͤhe in a ist; so muͤssen die correspondirenden
Punkte, von b aus gesehen, genau in einer geraden
Linie liegen, wenn die Refraktion neutral ist; und so kann ihr Einfluß
fuͤr jede gegen den Horizont geneigte, also auch fuͤr die zu
messende Linie genau bestimmt werden. Wenn man an vielen Orten eine solche
Vorrichtung treffen wuͤrde, die Refraktion der Atmosphaͤre zu
bestimmen, so koͤnnte man, glaube ich, manche Aufschluͤsse
uͤber den Zustand der Atmosphaͤre selbst erhalten, und eine solche
Vorrichtung wuͤrde an der Seite eines Barometers, Thermometers,
Hygrometers etc. vielleicht nicht ganz am unrechten Plaze seyn.
II. Astronomische Wage.
Dieses Instrument scheint mir vorzuͤglich zu folgenden Zweken anwendbar zu
seyn.
1) Laͤßt sich die Attraction des Mondes genauer messen als bisher
geschehen ist; denn da sich die Differenz derselben fuͤr zwei um den
Durchmesser der Erde verschiedene Abstaͤnde messen laͤßt (siehe
§. 5. N. 1.), so laͤßt sich auch die
Kraft selbst bestimmen, wenn die Entfernung des Mondes von der Erde bekannt ist.
– Aus dieser Attractionskraft laͤßt sich dann auch die Masse des
Mondes und seine Dichtigkeit berechnen.
2) Laͤßt sich die Frage beantworten, „ob alle Materie gleich
gravitire oder nicht;“ d.h. nicht nur die einzelnen Materien der
Erde unter sich,
sondern auch gegen den Mond, gegen die Sonne etc., wie ich schon §. 5.
N. 3 angedeutet habe.
3) Laͤßt sich die Groͤße der Erde auf viel leichterem Wege als
gewoͤhnlich und, wie ich glaube, viel genauer bestimmen, und zwar auf
folgende Art:
Aus §. 5. N. 2 sieht man, daß die Kraft, mit
welcher ein Koͤrper sich wegen der Axendrehung der Erde gegen
Suͤden bewegt, oder eigentlich die Differenz derselben in verschiedenen
Hoͤhen, gemessen werden koͤnnen. Wenn nun aber der Abstand PQ (siehe §. 5. N. 2), die geographische Breite des Ortes und die Kraft (oder
eigentlich die Differenz derselben) bekannt sind, so laͤßt sich der
Radius der Erde selbst finden.
Es sey die Schwungkraft am Aequator
= G/289
der Sinus der geographischen Breite
= a
der Cosinus der geographischen Breite =
α
die Schwungkraft fuͤr diesen Ort
=
g
Diese wird nun in zwei Theile zerlegt, wovon der eine Theil in der Richtung der
Tangente, also gegen den Aequator wirkt; sie sey = g'. Nun werde der Standpunkt um PQ = d erhoͤht; so wird auch die Kraft g' groͤßer und sey = g''; also die Differenz derselben oder g''
– g' = D; so verhaͤlt
sich
Textabbildung Bd. 43, S. 91
Wenn nun die geographische Breite bekannt ist, so ist natuͤrlich (a . α)/r² gegeben, obwohl weder a, noch α, noch
r bekannt sind und es sey (a + α)/r² = b, so ist
D = bd/r + G/289 und r = bdG/(D . 289), oder wenn G =
1 ist, so ist r = bd/(289D).
Es sey z.B. die geographische Breite = 45°, also b = 1/2; es sey d = 500 Fuß; D = 1/20000000 G; so ist
r = ½ 500/289; 1/20000000 =
10000000000/578 = 17300000 Fuß ungefaͤhr.
Bei dieser Art zu messen laͤßt sich bd so
genau bestimmen, daß die Fehler verschwinden, und es haͤngt daher Alles
von der genauen Bestimmung der Groͤße D ab.
Ließe sich D so genau bestimmen, daß man noch den
20000,000sten Theil derselben angeben koͤnnte, so waͤre der
Halbmesser der Erde bei einem Fuß genau gemessen; ließe sich aber D nur so genau bestimmen, daß man nur den 1000sten
Theil derselben angeben koͤnnte, so waͤre auch v nur bei 20,000 Fuß genau bestimmt. –
Um nun zu untersuchen, wie genau D bestimmt werden
kann, so sey PQ (siehe §. 5 N. 2) = 500 Fuß; der Hebelarm 200 Fuß lang, und habe
eine Schwingungskraft von 100 Sekunden; so ist, wenn b = 1/2, r = 17300000 ist,
D = 500/2,17300000,289 = 1/20000000
und aus der Gleichung (siehe §. 4) γ = α/λn² G ist
(γ = D) a = γλn²/g =
1,306,100000/20000000 = 15, etc. etc. Fuß.
Nun aber laͤßt sich mit einem Mikroskop von 100maliger
Linearvergroͤßerung noch 0,001 Linie, also 0,00001 Schuh, daher D/1500000
noch genau angeben, und daher der Halbmesser der Erde 1500000 bei einer
Genauigkeit = 20000000/1500000 = 13 Fuß bestimmen.
Da hier die Muͤhe, die man hat, gar nicht in Verhaͤltniß zu sezen
ist mit derjenigen, die Groͤße auf irgend eine andere Art zu bestimmen;
da ferner diese Operation zu jeder Tages- und Jahreszeit gemacht werden
kann, und in kurzer Zeit sich wiederholen und abaͤndern laͤßt,
wobei man gar nichts als die in §. 3. genannten Punkte zu beobachten hat;
so scheint es mir wirklich der Muͤhe werth zu seyn, einmal im Großen eine
solche Messung vorzunehmen, und ich kann mich der Aeußerung des Wunsches nicht
enthalten, daß ein Instrument dieser Art an irgend einem Orte recht bald
realisirt werden moͤchte.
Tafeln